Лекция 8, 1-й курс. Лекция 8 11. 2021 Второе начало (закон) термодинамики
 Скачать 170.99 Kb. Скачать 170.99 Kb.
|
Лекция 81.11.2021 Второе начало (закон) термодинамики1. Некоторые формулировки второго начала термодинамикиПо мере развития термодинамики этот закон (начало), как обобщение опытных фактов, формулировался разными учеными по-разному, но все эти формулировки отражали необратимость протекания процессов в природе. Приведем некоторые из этих формулировок. 1. Невозможен процесс, единственным результатом которого является переход тепла от холодного тела к горячему (Клаузиус). 2. Невозможен вечный двигатель второго рода, т.е. такое устройство, которое превращало бы тепло в работу полностью (Оствальд). 3. Невозможен процесс самопроизвольного перехода тепловой энергии в другие виды энергии. 2. Энтропия в термодинамикеРяд термодинамических формулировок второго начала термодинамики содержит понятие энтропии системы. При развитии термодинамики оказалось, что помимо внутренней энергии системы функцией состояния системы также является величина, которая для равновесных процессов вводится (это было сделано Клаузиусом) по формуле 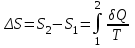 , , 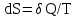 . (2.53) . (2.53)Следовательно, эта величина не зависит от пути перехода из одного состояния в другое, она получила название энтропия. Величину ( 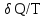 ) в формуле (2.53) называют приведенной теплотой. ) в формуле (2.53) называют приведенной теплотой. Из формулы (2.53) следует, что источником изменения энтропии системы является теплообмен между системой и внешними телами. В зависимости от вида равновесного процесса, происходящего в системе, энтропия системы может как возрастать (тепло подводится к системе), так и убывать (тепло отводится от системы). Оказалось, что существует еще один источник изменения энтропии, он связан с протеканием в системе неравновесного процесса. Клаузиус показал, что при протекании неравновесного процесса в замкнутой (изолированной) системе ее энтропия возрастает. Поэтому для изменения энтропии системы с учетом возможности протекания в ней неравновесного процесса равенство (2.53) запишется следующим образом: 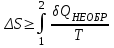 . (2.54) . (2.54)Эта формула (2.54) является важной для анализа протекания необратимых процессов в замкнутых (или изолированных) системах (нет теплообмена между системой и окружающими телами – 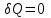 ), для них ), для них 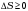 . .Дадим формулировку второго начала термодинамики с использованием понятия энтропии (Клаузиус): энтропия замкнутой системы стремится к максимуму: 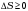 . (2.55) . (2.55)Из опыта известно, что если замкнутая (или изолированная) система сначала находилась в неравновесном состоянии, то с течением времени в ней протекают процессы перехода в равновесное состояние, в состояние теплового равновесия. При таком процессе энтропия системы возрастает 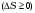 . Когда система переходит в равновесное состояние, энтропия достигает максимального значения, которое с течением времени остается неизменным. . Когда система переходит в равновесное состояние, энтропия достигает максимального значения, которое с течением времени остается неизменным. 3. Расчет изменения энтропии для изопроцессовФормулы (2.41), (2.53) позволяют рассчитать изменение энтропии для разных изопроцессов. Изотермический процесс: 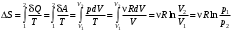 . (2.56) . (2.56)Изохорический процесс: 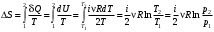 . (2.57) . (2.57)Изобарический процесс: 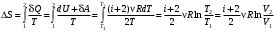 (2.58) (2.58)Адиабатный процесс: Так как теплота не подводится ( 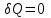 ), во всех равновесных адиабатных процессах ), во всех равновесных адиабатных процессах 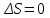 , S=const. (2.59) , S=const. (2.59)Такие процессы называются изоэнтропийными. ЭЛЕКТРостатика1. Электрический заряд. Закон КулонаЭлектростатика – раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов. Электрический заряд – это скалярная физическая величина, характеризующая способность тел вступать в электромагнитные взаимодействия, величина которой определяет интенсивность этих взаимодействий. Электрический заряд дискретен, т.е. заряды всех тел и частиц, вступающих в электромагнитные взаимодействия, кратны элементарному заряду (минимальному, существующему в природе) заряду. 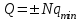 , (3.1) , (3.1)где 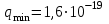 – величина элементарного заряда,N – целое число. – величина элементарного заряда,N – целое число.Электрический заряд обладает свойством аддитивности: заряд любой системы есть алгебраическая сумма зарядов частиц, составляющих эту систему. В электрически изолированных системах справедлив закон сохранения электрического заряда: суммарный заряд электрически изолированной системы остается неизменным  . (3.2) . (3.2)Введение электрического заряда позволило сформулировать закон Кулона: силы, с которыми взаимодействуют два неподвижных точечных заряда в вакууме, прямо пропорциональны произведению их зарядов и обратно пропорциональны квадрату расстояния между ними; силы направлены вдоль прямой, соединяющей эти заряды (рис. 3.1,): 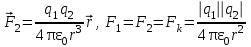 . (3.3) . (3.3)где 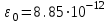 Ф/м –электрической постоянной. Ф/м –электрической постоянной. 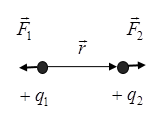 Рис. 3.1 При взаимодействии электрических зарядов в среде сила их взаимодействия уменьшается в 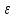 раз, где раз, где 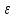 – относительная диэлектрическая проницаемость среды. Тогда выражение (3.3) имеет вид – относительная диэлектрическая проницаемость среды. Тогда выражение (3.3) имеет вид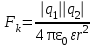 (3.4) (3.4)Относительная диэлектрическая проницаемость для вакуума равна единице; для каждой среды 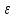 имеет свое значение большее единицы (ε>1), однако для воздуха имеет свое значение большее единицы (ε>1), однако для воздуха 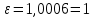 . .2. Вектор напряженности |

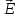 электростатического поля
электростатического поля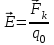 (3.5)
(3.5)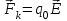 . (3.6)
. (3.6)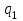 , а в качестве заряда находящегося в этом поле – точечный заряд
, а в качестве заряда находящегося в этом поле – точечный заряд 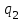 . Используя формулы (3.4), (3.6) получим
. Используя формулы (3.4), (3.6) получим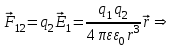
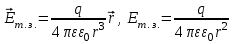 (3.7)
(3.7)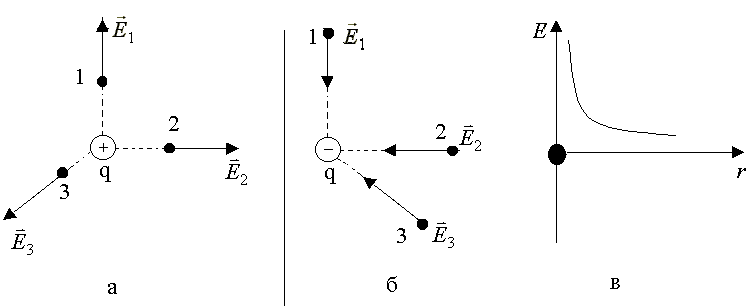
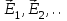 ) [3].
) [3].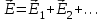 (3.8)
(3.8)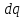 ). Затем по формуле (3.7) в точке А найти вектора
). Затем по формуле (3.7) в точке А найти вектора 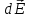 от этих зарядов и просуммировать их, т.е. взять интеграл по всему объему Vтела
от этих зарядов и просуммировать их, т.е. взять интеграл по всему объему Vтела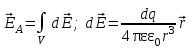 . (3.9)
. (3.9)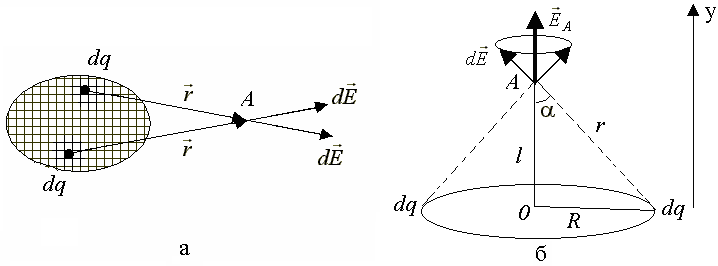
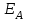 формулу (3.9). Из симметрии задачи видно, что все вектора
формулу (3.9). Из симметрии задачи видно, что все вектора 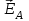 будет направлен вдоль оси, вверх [3].
будет направлен вдоль оси, вверх [3]. 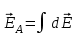 ;
;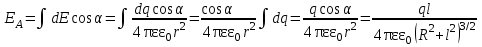 ;
;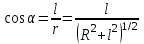 .
.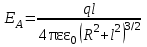 ; (3.10)
; (3.10)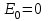 . (3.11)
. (3.11)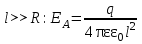 .
.