Лекция 8 Элементарные излучатели Вопрос Элементарный электрический вибратор. Вопрос Элементарный магнитный вибратор
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
Лекция №8 «Элементарные излучатели» Вопрос 1. Элементарный электрический вибратор. Вопрос 2. Элементарный магнитный вибратор. Введение Объемная плотность тока в излучающей системе, определяющая характеристики и параметры антенны, зависит от конструкции антенны, способа ее запитки, электрических свойств материалов и для многих применяемых в настоящее время антенн может иметь довольно сложный характер. Поэтому для выяснения некоторых общих закономерностей, свойственных характеристикам и параметрам антенн, целесообразно выяснить основные свойства простейших излучателей: точечных (малых волновых размеров), линейных, плоских, имеющих непрерывное или дискретное распределение тока. Анализ простейших излучателей имеет большое методологическое значение, так как согласно принципу суперпозиции любую сложную антенну можно представить в виде определенной совокупности простейших излучателей. Следовательно, характеристики и параметры сложных в конструктивном отношении антенн определяются характеристиками и параметрами составляющих их простейших излучающих элементов. ЭЛЕМЕНТАРНЫЕ ИЗЛУЧАТЕЛИ Элементарными принято называть излучатели малых волновых размеров. В пределе ( 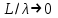 , где L - характерный габаритный размер излучателя) такие излучатели являются точечными. На ранних этапах развития антенной техники (первая четверть ХХ века) практически все антенны имели малые размеры по сравнению с применяющимися рабочими длинами волн. В зависимости от характера тока в излучающей системе элементарные излучатели являются электрическими, магнитными или их комбинациями. , где L - характерный габаритный размер излучателя) такие излучатели являются точечными. На ранних этапах развития антенной техники (первая четверть ХХ века) практически все антенны имели малые размеры по сравнению с применяющимися рабочими длинами волн. В зависимости от характера тока в излучающей системе элементарные излучатели являются электрическими, магнитными или их комбинациями.1. Элементарный электрический вибратор Элементарным электрическим вибратором (электрическим диполем, диполем Герца) называют прямолинейный излучатель малого волнового размера с равномерным распределением амплитуды возбуждающего электрического тока. Согласно уравнению непрерывности в электродинамике (третье уравнение Максвелла) равномерное распределение амплитуды тока в прямолинейном тонком проводнике может иметь место лишь при наличии сосредоточенных электрических зарядов на его концах (электрический диполь). Этому условно приближенно отвечает конструкция (рис. 1, а), включающая два металлических шарика, соединенных тонким проводником. Вектор объемной плотности электрического тока в такой конструкции ориентирован вдоль оси диполя, а амплитуда тока 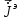 в диполе примерно постоянна (рис. 1, б). в диполе примерно постоянна (рис. 1, б).Для расчета поля, создаваемого элементарным электрическим вибратором, введем декартову систему координат, сориентировав ось z вдоль вибратора (рис. 1, а). С учетом малых волновых размеров вибратора вдоль любой из координатных осей и заданной ориентации тока в нем объемную плотность электрического тока запишем в виде 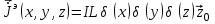 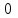 , (1) где I, А - амплитуда тока в вибраторе; IL, Ам - электрический момент диполя. Р 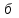 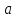 ис. 1. Элементарный электрический вибратор (а) и амплитудное ис. 1. Элементарный электрический вибратор (а) и амплитудноераспределение тока в нем (б) Подставляя равенство (1) в формулу для магнитного и векторного потенциалов (см. лекцию 7): 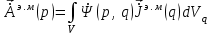 и учитывая, что в прямоугольной системе координат 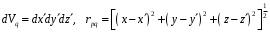 , после вычисления интеграла получаем следующее выражение для электродинамического потенциала: , после вычисления интеграла получаем следующее выражение для электродинамического потенциала: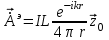 , (2.2) , (2.2)где 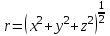 . .См. рисунок к лекции № 7 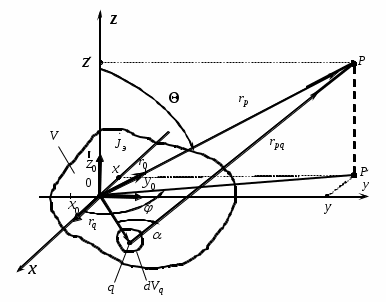 Проекция вектора 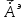 на оси сферической системы координат с учетом того, что в рассматриваем случае на оси сферической системы координат с учетом того, что в рассматриваем случае 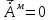 согласно формулам согласно формулам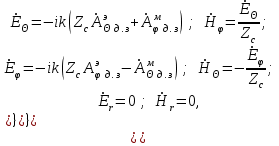 определяют соответствующие компоненты векторов поля. Для вычисления указанных проекций необходимо орт 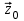 выразить через орты выразить через орты 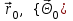 и и 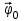 сферической системы координат. Связь прямоугольных и сферических ортов выражается следующим матричным равенством [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. 720 с.]: сферической системы координат. Связь прямоугольных и сферических ортов выражается следующим матричным равенством [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. 720 с.]: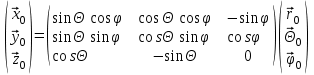 . (3) . (3)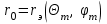 - расстояние до эквифазной поверхности вдоль направления максимального излучения. - расстояние до эквифазной поверхности вдоль направления максимального излучения.Отсюда находим 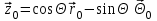 . (4) . (4)Учитывая соотношения (2) и (4) в формулах (22), предоставленной в лекции 7, получаем следующее выражение для вектора напряженности электрического поля в дальней зоне: 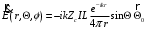 . (5) . (5)В связи с тем, что угол 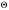 определяет пространственное положение точки приема P в сферической системе координат, то введем функцию, определяющую направленные свойства элементарной площадки излучающей системы в точке q и назовём ее амплитудной диаграммой направленности (АНД) элементарного электрического вибратора: определяет пространственное положение точки приема P в сферической системе координат, то введем функцию, определяющую направленные свойства элементарной площадки излучающей системы в точке q и назовём ее амплитудной диаграммой направленности (АНД) элементарного электрического вибратора: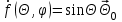 . (6) . (6)Отсюда находим 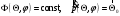 . (7) . (7)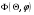 - фазовая диаграмма направленности излучателя (ФДН). - фазовая диаграмма направленности излучателя (ФДН).В формуле (7) ФДН постоянная значит элементарный излучатель излучает сферическую волну. Таким образом, АДН элементарного электрического вибратора, размещенного в центре системы координат, не зависит от угла 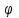 , что является следствием осевой симметрии этого излучателя (симметрии левого и правого плеча излучающей системы антенны). Сечения АДН главными плоскостями описываются выражениями: , что является следствием осевой симметрии этого излучателя (симметрии левого и правого плеча излучающей системы антенны). Сечения АДН главными плоскостями описываются выражениями: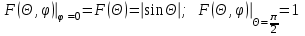 . (8) . (8)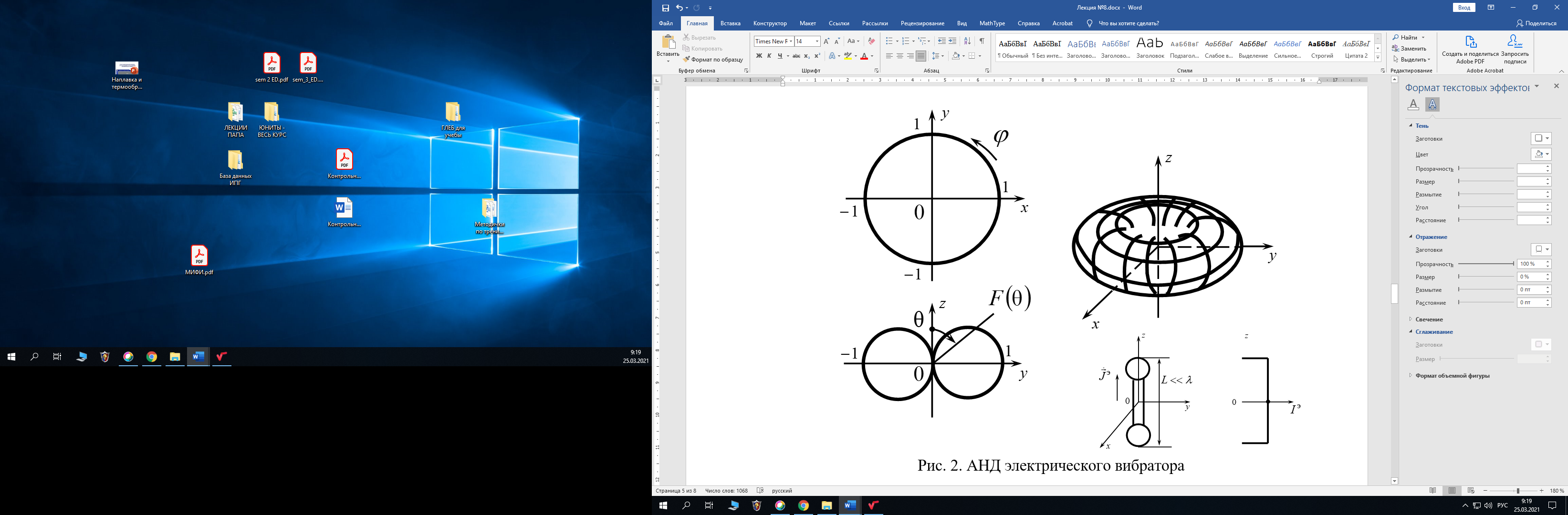 Рис. 2. АНД электрического вибратора Изображения плоскостных и пространственной АДН элементарного вибратора представлены на рис. 2. Максимумы АДН в любой вертикальной плоскости, проходящей через ось диполя (OZ), ориентированы под углами 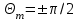 , т.е. по нормали к вибратору. Вдоль оси вибратор не излучает. Из условия , т.е. по нормали к вибратору. Вдоль оси вибратор не излучает. Из условия 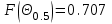 находим находим 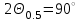 . .Фазовая диаграмма элементарного электрического вибратора в силу соотношений представляет сферическую поверхность. Рассматриваемый излучатель имеет фазовый центр, совпадающий с началом выбранной системы координат - центром диполя (рис. 1). Излучаемая мощность и сопротивление излучения Мощность излучения ЭЭВ определяется формулой 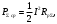 где 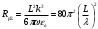 – сопротивление излучения ЭЭВ. – сопротивление излучения ЭЭВ.2. Элементарный магнитный вибратор Элементарный магнитный вибратор (магнитный диполь) является прямолинейным излучателем малых волновых размеров и отличается от электрического вибратора лишь тем, что точечной является объемная плотность магнитного тока: 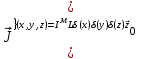 , (10) , (10)где 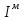 , В - амплитуда магнитного тока; , В - амплитуда магнитного тока; 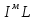 , Вм - магнитный момент. , Вм - магнитный момент. Рис. 3. Связь объемных плотностей электрического и магнитного токов в кольцевом проводнике Определим физическую модель излучателя, имеющего объемную плотность магнитного тока вида (10). С помощью равенств (2) и (5), связывающих объемную плотность магнитного тока с вихревой составляющей электрического тока, можно установить, что объемная плотность магнитного тока близка к точечной, когда  имеет кольцевой характер (рис. 3). При этом радиус а кольца с током должен быть бесконечно малым (практически достаточно имеет кольцевой характер (рис. 3). При этом радиус а кольца с током должен быть бесконечно малым (практически достаточно  ). Итак, элементарный магнитный вибратор с объемной плотностью магнитного тока вида (10) может быть реализован с помощью кольцевого проводника (рамки) малого радиуса, в котором протекает ток с амплитудой I, величина которой не изменяется вдоль проводника. Величина магнитного момента ). Итак, элементарный магнитный вибратор с объемной плотностью магнитного тока вида (10) может быть реализован с помощью кольцевого проводника (рамки) малого радиуса, в котором протекает ток с амплитудой I, величина которой не изменяется вдоль проводника. Величина магнитного момента  связана с амплитудой тока в рамке и ее размером соотношением [Марков Г.Т., Сазонов А.М. Антенны. М.: Энергия, 1975, Сазонов Д.М. Антенны и устройства СВЧ. М.: Высшая школа, 1988]: связана с амплитудой тока в рамке и ее размером соотношением [Марков Г.Т., Сазонов А.М. Антенны. М.: Энергия, 1975, Сазонов Д.М. Антенны и устройства СВЧ. М.: Высшая школа, 1988]: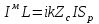 , (11) , (11)где 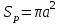 - площадь рамки. - площадь рамки.Реализация элементарного магнитного вибратора в виде кольцевого проводника не является единственно возможной. Кольцевую форму, в частности, может иметь не ток проводимости, а ток смещения. Ток смещения кольцевой формы создается, например, вокруг щели, прорезанной в проводящем экране больших (теоретически - бесконечных) размеров (рис. 4). При этом вектор напряженности магнитного поля 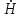 , а вместе с ним в силу равенства (1.5) и объемная плотность магнитного тока , а вместе с ним в силу равенства (1.5) и объемная плотность магнитного тока 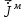 будут ориентированы вдоль щели. Если размеры щели малы по сравнению с длиной волны, то амплитуда магнитного тока будут ориентированы вдоль щели. Если размеры щели малы по сравнению с длиной волны, то амплитуда магнитного тока 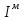 будет примерно постоянной вдоль щели. Для более строгого выполнения этого условия на краях щели прорезаются небольшие круглые отверстия, роль которых аналогична роли шариков на концах электрического вибратора. будет примерно постоянной вдоль щели. Для более строгого выполнения этого условия на краях щели прорезаются небольшие круглые отверстия, роль которых аналогична роли шариков на концах электрического вибратора.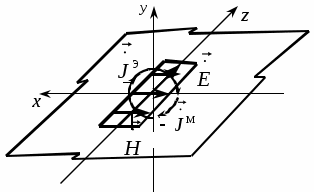 Рис. 4. Магнитный ток в щели Математическое описание кольцевых электрических токов сложнее, чем соответствующих им линейных магнитных. Поэтому введение магнитного тока является приемом, упрощающим расчет рамочных и щелевых излучателей. Поле, создаваемое элементарным магнитным вибратором, можно определить с использованием общих соотношений (7), (9). Однако практически удобнее воспользоваться принципом перестановочной двойственности. Тогда на основании соотношения (5) с учетом того, что 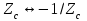 , получаем , получаем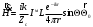 . (12) . (12)Из формул (5) и (12) следует, что диаграммы направленности элементарных магнитного и электрического вибраторов совпадают. Равенство амплитудных диаграмм направленности элементарных электрического и магнитного вибраторов означает и равенство их КНД. Излучаемая мощность и сопротивление излучения Мощность излучения рамки находится так же, как мощность излучения элементарного электрического вибратора, и определяется формулой 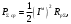 где 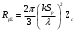 – сопротивление излучения рамки. – сопротивление излучения рамки.По определению 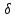 -функции -функции 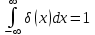 . Отсюда следует, что размерность . Отсюда следует, что размерность 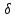 -функции с пространственным аргументом (точнее, коэффициента перед ней, равного по величине единице) обратна размерности длины. Следовательно, с учетом размерности электрического момента диполя размерность объемной плотности электрического тока будет -функции с пространственным аргументом (точнее, коэффициента перед ней, равного по величине единице) обратна размерности длины. Следовательно, с учетом размерности электрического момента диполя размерность объемной плотности электрического тока будет 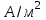 . . |
