Лекция Арифметические и логические основы компьютеров
 Скачать 31.18 Kb.
|
|
Лекция 9. Арифметические и логические основы компьютеров.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”). Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности. Существуют позиционные и непозиционные системы счисления. Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления. Логика – наука, изучающая законы и формы мышления. Алгебра логики это математический аппарат , с помощью которого записывают, упрощают, преобразовывают и вычисляют логические высказывания. Это раздел математики, который изучает высказывания с точки зрения их логических значений и логических (операций)связок. Впервые АЛ, как математический аппарат возникла в середине 19 века в трудах английского математика Джорджа Буля и с тех пор носит название «булева алгебра». Логическое высказывание это любое повествовательное предложение, в отношение которого можно сказать однозначно истинно оно или ложно. Рим – столица Италии (истина), 5 – четное число (ложь). Кроме того, в АЛ используются и сложные высказывания, которые содержат несколько простых мыслей, соединенных между собой (связками) логическими операциями. Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение: НЕ - Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием (или знаком  ). Высказывание истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна - спутник Земли" (А); "Луна - не спутник Земли" ( ).И - Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio - соединение) или логическим умножением и обозначается точкой "  " (может также обозначаться знаками или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание: "10 делится на 2 и 5 больше 3" истинно, а высказывания : "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" - ложны.ИЛИ - Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio - разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5" ложно, а высказывание "10 делится на 2 или 10 делится на 3", - истинно. Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, (называемые также вентилями), а также триггер. Имеется один или несколько входов и один выход. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности. Таблица истинности - это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений входных сигналов (операндов) и соответствующие им значения выходного сигнала (результата операции) для каждого из этих сочетаний.  Рис.1 Схема И Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис 1. Таблица истинности схемы И
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y (читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and. 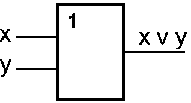 Рис. 2 Схема ИЛИ Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица. Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис.2. Обозначение - знак "1" на схеме Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y"). Таблица истинности схемы ИЛИ
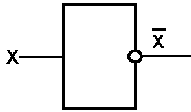 Рис. .3 Схема НЕ Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =  , где читается как "не x" или "инверсия х".Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора - на рисунке 3 Таблица истинности схемы НЕ
|
