Лекция. Лекция №10-11 (8 неделя -3 часа). Лекция числовые характеристики поездных токов
 Скачать 194.42 Kb. Скачать 194.42 Kb.
|
|
Лекция 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ПОЕЗДНЫХ ТОКОВ Прежде чем перейти к расчету средних и эффективных токов фидеров и подстанции, потерь напряжения и потерь энергии в тяговой сети, остановимся на определении применяемых в расчетах числовых характеристик токов поездов, так как последние являются исходными при расчетах всех перечисленных выше величин. Токи поездов непрерывно меняются. В этих случаях принято характеризовать ток поезда двумя величинами: средним и эффективным (т. е. средним квадратичным) значениями. Все приводимые ниже формулы выведены для системы постоянного тока. Однако они могут быть использованы и для системы переменного тока. Для этой цели надо все поездные токи, получаемые на основе тяговых расчетов, представить в виде отдельных двух графиков активных и реактивных составляющих и далее все полученные формулы относить отдельно к той и другой составляющим. Средние и эффективные токи поездов при отсутствии рекуперации энергии. При использовании тяговых расчетов может быть найдено среднее значение тока для каждого типа поезда как средняя ордината 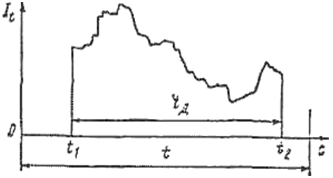 Рис. 7.1. К определению средних и эффективных значений токов поездов:  - время хода поезда по участку; - время хода поезда по участку;  - время потребления энергии поездом - время потребления энергии поездомкривой  (рис. 7.1) и среднее квадратичное значение тока поезда по кривой (рис. 7.1) и среднее квадратичное значение тока поезда по кривой 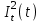 . При переменном токе среднее значение является комплексной величиной, состоящей из средних значений составляющих, а среднее значение квадрата тока поезда (квадрат эффективного значения) - суммой их квадратов. При равных углах сдвига фаз всех грузок расчет можно вести по полному току. . При переменном токе среднее значение является комплексной величиной, состоящей из средних значений составляющих, а среднее значение квадрата тока поезда (квадрат эффективного значения) - суммой их квадратов. При равных углах сдвига фаз всех грузок расчет можно вести по полному току.Если же кривых потребления тока поездами нет, то среднее значение тока может быть найдено по заданному расходу энергии и напряжению тяговой сети 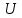 . Определение эффективного значения тока в этом случае затрудняется. Однако при наличии данных о средних значениях тока поезда за все время хода по рассматриваемому участку (блок-участку, перегону, фидерной или подстанционной зоне), времени хода его и времени потребления им энергии на этом участке с достаточной точностью можно установить и соответствующее эффективное значение тока. К тому же определение средних и эффективных значений токов поездов по кривым . Определение эффективного значения тока в этом случае затрудняется. Однако при наличии данных о средних значениях тока поезда за все время хода по рассматриваемому участку (блок-участку, перегону, фидерной или подстанционной зоне), времени хода его и времени потребления им энергии на этом участке с достаточной точностью можно установить и соответствующее эффективное значение тока. К тому же определение средних и эффективных значений токов поездов по кривым 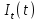 и и 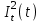 , даже если эти кривые имеются, требует большой кропотливой работы по планиметрированию площадей, образуемых этими кривыми и осью абсцисс. Кроме того, обычно в тяговых расчетах даются кривые не по времени, а по пути, что требует еще и перестройки их. Поэтому желательно получить искомые значения поездных токов более простым путем, конечно, с достаточной для практических целей точностью. , даже если эти кривые имеются, требует большой кропотливой работы по планиметрированию площадей, образуемых этими кривыми и осью абсцисс. Кроме того, обычно в тяговых расчетах даются кривые не по времени, а по пути, что требует еще и перестройки их. Поэтому желательно получить искомые значения поездных токов более простым путем, конечно, с достаточной для практических целей точностью.При движении поезда по участку энергия потребляется поездом не непрерывно, так как имеются различные режимы движения (тяга, выбег, торможение) в зависимости от профиля и других условий движения. Рассмотрим кривую 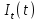 (см. рис. 7.1) для некоторого участка (например, перегона). Среднее значение тока поезда за время (см. рис. 7.1) для некоторого участка (например, перегона). Среднее значение тока поезда за время 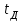 потребления энергии потребления энергии 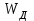 можно найти из выражения можно найти из выражения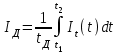 , или , или 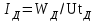 , (7.1) , (7.1)При переменном токе 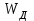 определяется по определяется по 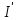 , а для расчета по , а для расчета по 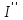 величина величина 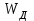 заменяется выражением заменяется выражением 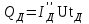 . .Среднее значение того же тока за время хода 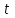 по рассматриваемому участку по рассматриваемому участку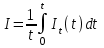 , или , или 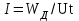 . (7.2) . (7.2)Из рис. 7.1 видно, что интегралы обоих выражений равны и поэтому 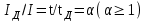 , тогда среднее значение тока поезда , тогда среднее значение тока поезда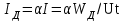 . (7.3) . (7.3)Квадрат эффективного значения тока поезда также за время потребления энергии и за все время хода выразится равенствами 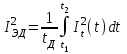 и и 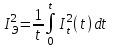 Вследствие равенства интегралов имеем: 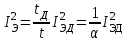 . (7.4) . (7.4)Обозначив 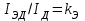 , получим: , получим: 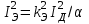 (здесь (здесь 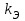 - коэффициент эффективности или коэффициент формы кривой поездного тока). Подставляя в последнее выражение полученное выше значение - коэффициент эффективности или коэффициент формы кривой поездного тока). Подставляя в последнее выражение полученное выше значение 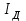 , окончательно напишем) , окончательно напишем)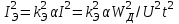 . (7.5) . (7.5)Обозначим 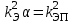 (здесь (здесь 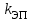 — коэффициент эффективности поездного тока). Величина а может быть всегда получена из тяговых расчетов или других материалов. Как показали многочисленные расчеты, значения — коэффициент эффективности поездного тока). Величина а может быть всегда получена из тяговых расчетов или других материалов. Как показали многочисленные расчеты, значения 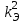 изменяются в очень узком диапазоне. В расчетах принимают изменяются в очень узком диапазоне. В расчетах принимают 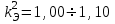 , причем большее значение для участков о резко меняющимся профилем или о частыми остановками (метрополитены, пригородные поезда). Примем значение , причем большее значение для участков о резко меняющимся профилем или о частыми остановками (метрополитены, пригородные поезда). Примем значение 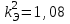 [7]. [7].Средние и эффективные токи поездов при рекуперации энергии. Приведенный способ определения эффективного, тока поездов основан на том, что значение коэффициента 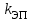 в основном зависит от соотношения времени потребления энергии и общего времени хода поезда. Изменение же кривой в период потребления тока оценивается коэффициентом в основном зависит от соотношения времени потребления энергии и общего времени хода поезда. Изменение же кривой в период потребления тока оценивается коэффициентом 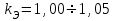 . Для определения эффективного тока поезда при применении рекуперативного торможения на линиях постоянного тока упрощенным способом примем, что на некотором участке (перегоне) кривая потребления тока имеет вид, представленный на рис. 7.2, а. Найдем среднее значение тока поезда и квадрат его эффективного значения. Условно расположим в одном интервале на оси времени суммарное время рекуперации, а в другом — суммарное время потребления энергии (рис. 7.2, б). При этом изменяющиеся токи заменим их средними значениями. Тогда, принимая во внимание рекуперативный режим, средний ток поезда / за все время его хода по данному участку . Для определения эффективного тока поезда при применении рекуперативного торможения на линиях постоянного тока упрощенным способом примем, что на некотором участке (перегоне) кривая потребления тока имеет вид, представленный на рис. 7.2, а. Найдем среднее значение тока поезда и квадрат его эффективного значения. Условно расположим в одном интервале на оси времени суммарное время рекуперации, а в другом — суммарное время потребления энергии (рис. 7.2, б). При этом изменяющиеся токи заменим их средними значениями. Тогда, принимая во внимание рекуперативный режим, средний ток поезда / за все время его хода по данному участку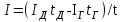 . (7.6) . (7.6)При определении эффективного тока поезда ордината квадратов тока рекуперации будет иметь тот же знак, что и ордината квадратов тяговых токов. Поэтому согласно формуле (7.5) имеем: 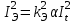 , (7.7) , (7.7)где 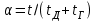 ; ; 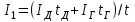 . .Средний же ток поезда, определяемый расходом энергии, должен находиться с учетом возврата энергии при рекуперации, т. е. этот средний ток должен рассчитываться по выражению (7.6), поэтому, очевидно, при рекуперации коэффициент эффективности поездного тока 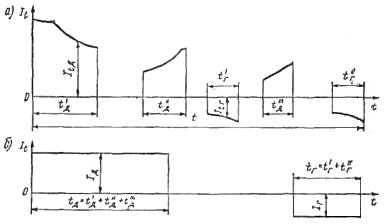 Рис. 7.2. К определению коэффициента эффективности поездного тока при рекуперативном торможении: 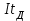 - значение тока для мгновенного расположения поездов а период потребления энергия; - значение тока для мгновенного расположения поездов а период потребления энергия; 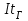 - то же в период рекуперации энергии; - то же в период рекуперации энергии; 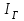 —среднее значение тока за время рекуперации —среднее значение тока за время рекуперации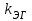 должен быть иным, чем при ее отсутствии. По аналогии с выражением (7.10) можно написать: должен быть иным, чем при ее отсутствии. По аналогии с выражением (7.10) можно написать: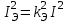 . (7.8) . (7.8)Сравнивая равенства (7.7) и (7.8), получим: 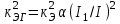 . .Подставляя в последнее выражение значения 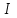 , , 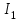 , и , и 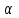 , получим: , получим: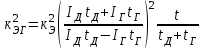 . (7.9) . (7.9)В этом выражении значение 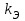 играет несколько меньшую роль, чем при отсутствии рекуперации (токи в период рекуперации мало изменяются), но можно принять его среднее значение также равным 1,08. Тогда квадрат коэффициента эффективности поездного тока при рекуперативном торможении играет несколько меньшую роль, чем при отсутствии рекуперации (токи в период рекуперации мало изменяются), но можно принять его среднее значение также равным 1,08. Тогда квадрат коэффициента эффективности поездного тока при рекуперативном торможении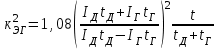 . (7.10) . (7.10)Если учесть, что 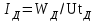 и и 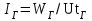 [здесь [здесь 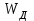 - расход энергии на тягу при отсутствии рекуперации; - расход энергии на тягу при отсутствии рекуперации; 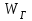 — энергия возвращенная в сеть при рекуперации; — энергия возвращенная в сеть при рекуперации; 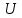 — среднее напряжение, при котором энергия потребляется или отдается локомотивом (обычно принимаемое равным номинальному)], то — среднее напряжение, при котором энергия потребляется или отдается локомотивом (обычно принимаемое равным номинальному)], то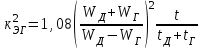 . (7.11) . (7.11)Если рекуперация отсутствует, т. е. 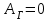 и и 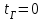 , то , то 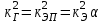 . Полученные формулы (7.9), (7.10) и (7.11) справедливы как для перегонов, так и для фидерных зон. При расчетах по реактивной составляющей переменного тока в формулах (7.6) - (7.11) знак минус изменяется на плюс, так как и при рекуперации электровоз потребляет реактивную мощность. . Полученные формулы (7.9), (7.10) и (7.11) справедливы как для перегонов, так и для фидерных зон. При расчетах по реактивной составляющей переменного тока в формулах (7.6) - (7.11) знак минус изменяется на плюс, так как и при рекуперации электровоз потребляет реактивную мощность.Средние и эффективные поездные токи фидеров (т. е. токи фидеров при одном поезде на участке). При схеме одностороннего питанием средний и эффективный токи поезда целиком относятся к данному фидеру, т. е. они равны соответствующим токам поездов. Если расчет для участков с двусторонним питанием ведут по данным кривым тока, то прежде всего следует кривую тока поезда paзложить на две, соответствующие двум подстанциям, и затем все расчеты вести, как для одностороннего питания, принимая во внимание для каждого фидера ту часть кривой поездного тока, которая относится к нему. Средний поездной ток фидера подстанции А (первый момент) за время хода поезда 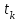 по перегону по перегону 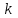 длиной длиной 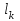 (рис. 7.3) определяется из выражения (рис. 7.3) определяется из выражения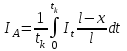 . .Соответственно квадрат эффективного поездного тока фидера (второй момент) за время хода поезда 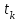 по перегону по перегону 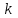 (длиной (длиной 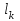 ) )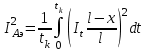 . .Если ток поезда в фидерной зоне принят постоянным и равным среднему значению, а скорость неизменной, то средний ток поезда делится между фидерами подстанций А и В пополам и определяет средний поездной ток фидера: 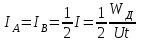 . (7.12) . (7.12)При этом условии квадраты эффективных поездных токов фидеров могут быть найдены из следующих соображений 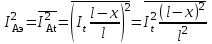 . .Здесь и ниже черта над величиной обозначает ее среднее значение (математическое ожидание). Не располагая зависимостью 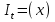 , примем допущение, что величины , примем допущение, что величины 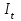 и и 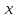 независимы. При этом можно заменить среднее значение произведения величин произведением их средних значений. Тогда о учетом того, что независимы. При этом можно заменить среднее значение произведения величин произведением их средних значений. Тогда о учетом того, что 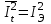 , получим: , получим: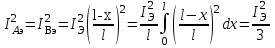 . (7.12а) . (7.12а)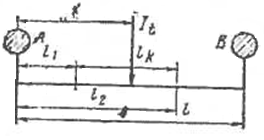 Рис. 7.3. Схема двустороннего питания одной нагрузки 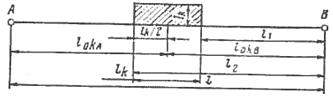 Рис. 7.4. К расчету средних токов поездов за время их хода по перегонам В этом случае при двустороннем питании можно определять квадрат эффективного поездного фидера (при отсутствии рекуперации) исходя из следующего. Подставив вместо 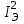 его значение из формулы (7.5) и заменив его значение из формулы (7.5) и заменив 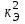 значением 1,0 - 1,1, получим: значением 1,0 - 1,1, получим: 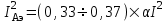 . Взяв среднее значение коэффициента, будем иметь: . Взяв среднее значение коэффициента, будем иметь: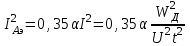 . (7.13) . (7.13)Выразив через средний поездной ток фидера согласно формуле (7.12), получим: 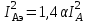 . (7.14) . (7.14)Если в фидерной зоне поезда потребляют значительно изменяющийся ток или это потребление имеет частые перерывы (метрополитены, пригородные участки, горные профили), то расчеты по средним токам поездов за время хода по фидерной зоне могут дать существенные погрешности. В этих случаях расчеты следует вести по средним токам поездов за время хода их по отдельным перегонам (блок-участкам). При этом среднее значение поездного тока фидера 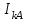 за время хода поезда по перегону за время хода поезда по перегону 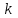 определится из следующих соображений (рис. 7.3). Если на некотором перегоне (блок-участке) определится из следующих соображений (рис. 7.3). Если на некотором перегоне (блок-участке) 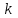 найдено среднее злачен не тока поезда найдено среднее злачен не тока поезда 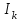 , то для определения поездного тока фидера можно считать, что сосредоточенная нагрузка, равная , то для определения поездного тока фидера можно считать, что сосредоточенная нагрузка, равная 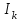 , приложена в середине данного перегона. Тогда , приложена в середине данного перегона. Тогда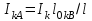 . (7.15) . (7.15)Квадрат эффективного поездного тока фидера за время хода поезда по перегону 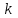 : :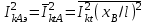 . .Здесь 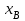 — расстояние точки приложения нагрузки тока — расстояние точки приложения нагрузки тока 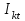 от подстанции В. от подстанции В.Считая, как и выше, величины 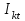 и и 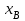 независимыми, получим) независимыми, получим) 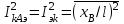 . Очевидно, что . Очевидно, что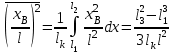 . .Так как 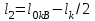 ; ; 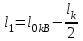 и и 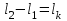 , то, отнеся выражение (7.5) к перегону , то, отнеся выражение (7.5) к перегону 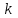 получим: получим: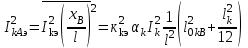 . (7.16) . (7.16)При числе перегонов в фидерной зоне более одного в последующих расчетах вторым членом в скобке вследствие его относительной малости можно пренебречь. |
