Курс лекций по электротехнике часть 1. Лекция элементы электрических цепей
 Скачать 1.05 Mb.
|
 Очевидно также, что  ,  .Видим, что полученные выражения полностью соответствуют (5.9) и (5.10). Это подтверждает единство физической сути различных видов резонанса. Определим ток и напряжение всей цепи , а также падение напряжения на ее отдельных элементах в режиме резонанса. Так как сопротивление всей цепи в режиме резонанса минимально и равно R то ток в ней максимален и равен  , (5.17)а падение напряжения определяется ЭДС источника - Е. Падение напряжения на отдельных элементах легко найти по закону Ома. Так, падение напряжения на резисторе R равно   (5.18)Тривиальный математически результат интересен по физической сути. Все напряжение источника выделяется на одном элементе цепи. Падение напряжения на индуктивности равно  (5.19)Величина  (5.20)называется добротностью и может принимать значение десятков и сотен единиц. Значит, падение напряжения на индуктивности может в десятки и сотни раз превышать ЭДС источника. Падение напряжения на емкости равно  (5.21)Так как  , то падение напряжения на емкости равно по величине падению напряжения на индуктивности, но согласно (5.8) они противоположны по знаку. Отношение напряжения на индуктивности или на емкости в режиме резонанса к току в этом режиме называют характеристическим сопротивлением  , причем (5.22)В силу того что  ,рассматриваемый режим назван резонансом напряжений. Противофазность напряжений   и  указывает на то, что в цепи происходит такой же колебательный процесс с частотой  , как и в параллельном колебательном контуре.Здесь также энергия источника затрачивается только на преодоление сопротивления резистора R. Поэтому цепь называется последовательным колебательным контуром. Завершим анализ резонанса напряжений разбором частотной зависимости тока цепи рис.5.5. и падений напряжений на элементах L и С от частоты (рис.5.6). На рисунке пунктиром отмечен график ЭДС. Падение напряжения на идеальной индуктивности при 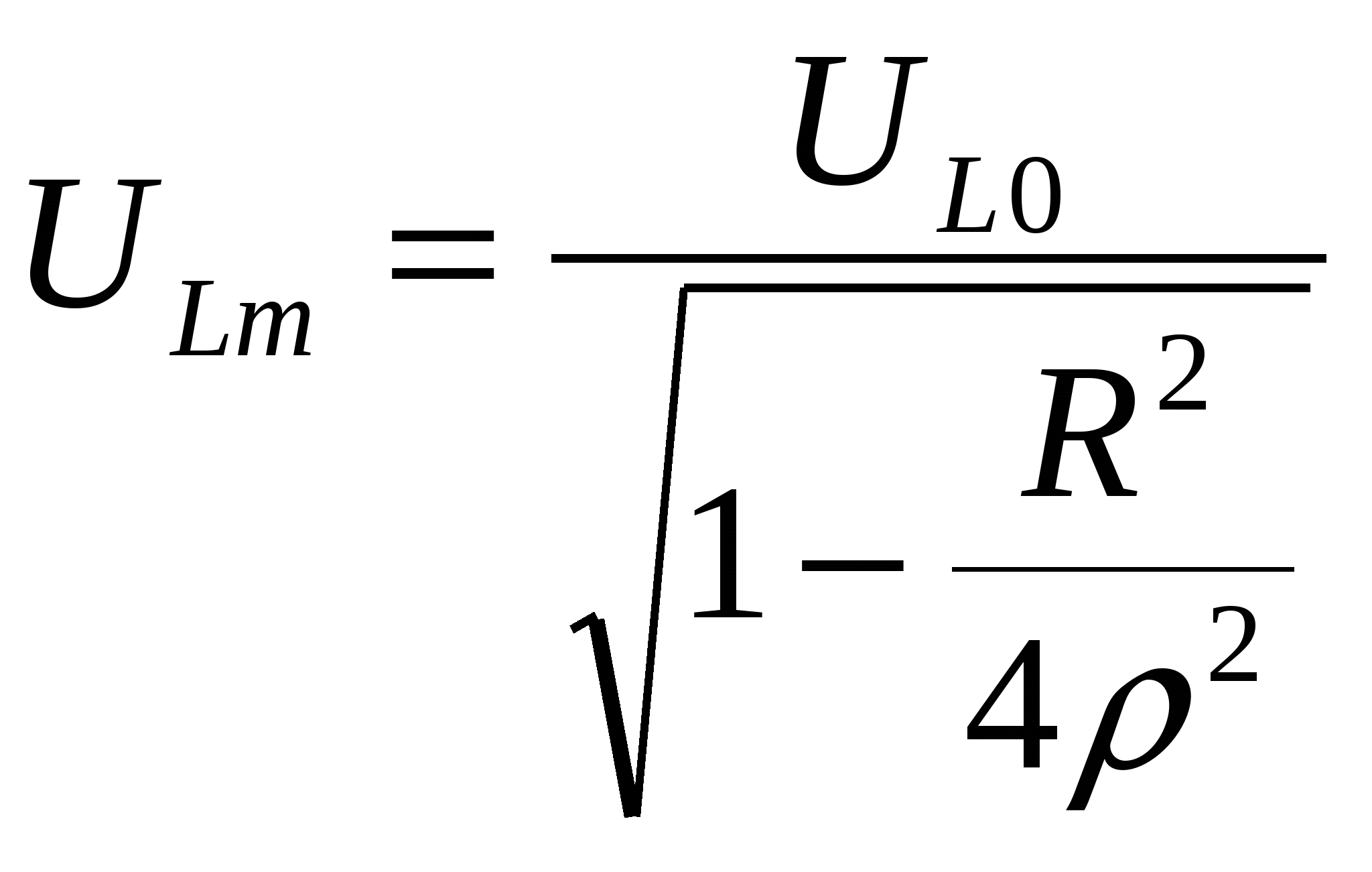 равно нулю. С увеличением частоты сопротивление индуктивности, а значит и падение напряжения на ней увеличивается. Когда частота устремляется в бесконечность сопротивление ХL также устремляется в бесконечность. При этом падение напряжения стремится к Е. Между крайними точками существует экстремум напряжения  который находится по формуле (5.23)Частота, на которой достигается этот максимум определяется выражением 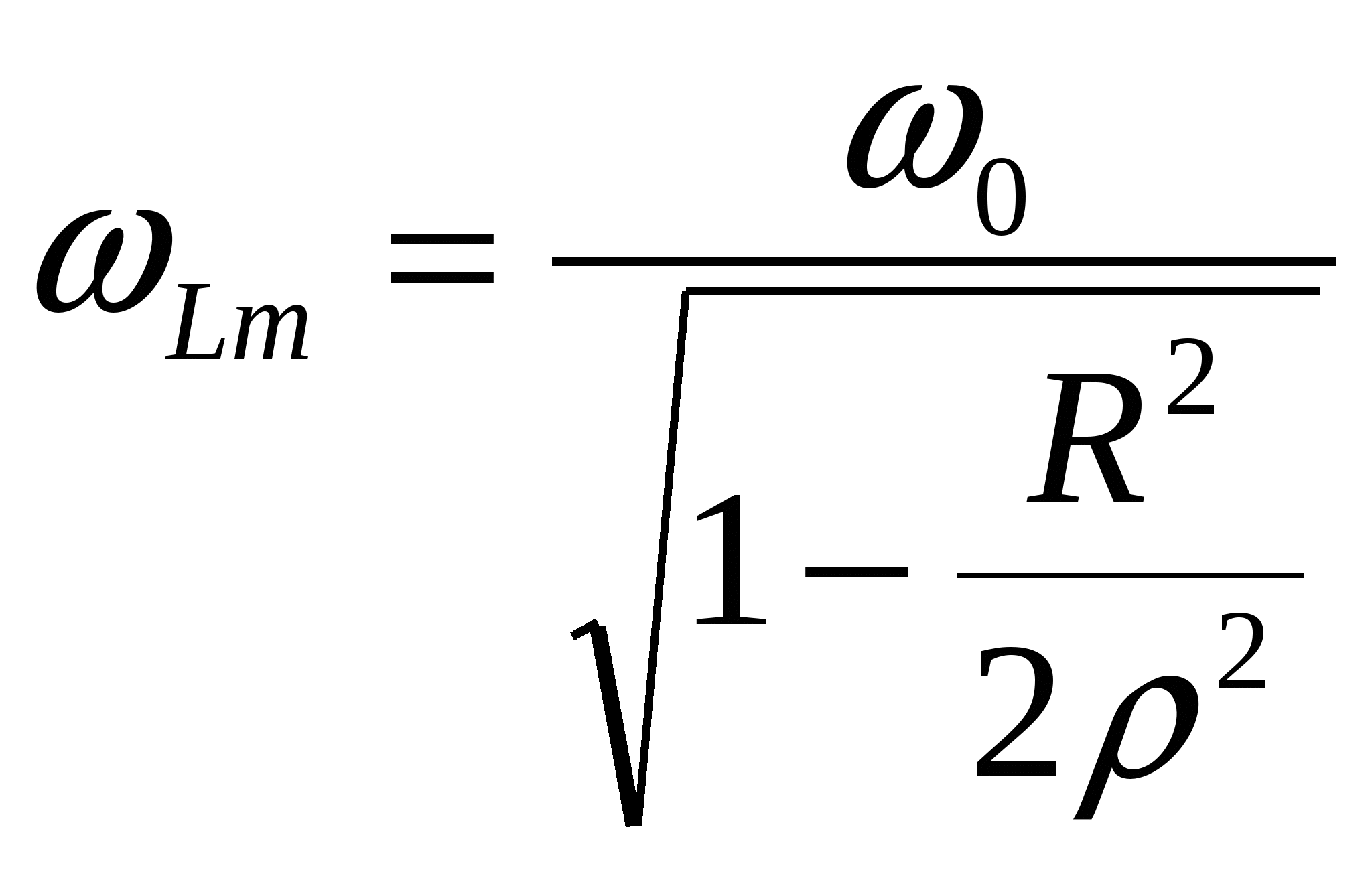 (5.24)Сопротивление емкости на частоте 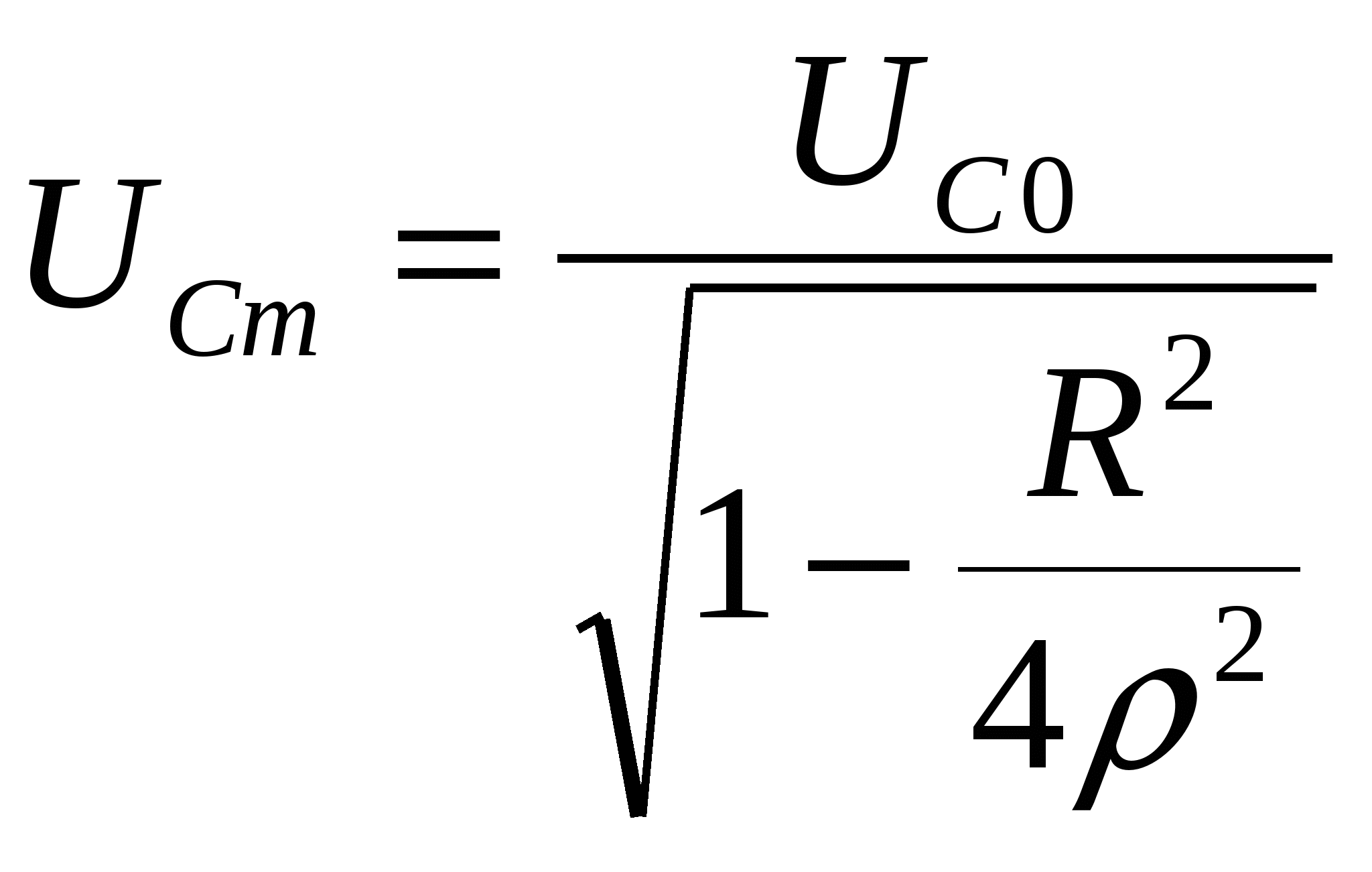равно бесконечности и значит напряжение на ее обкладках равно Е. С увеличением частоты сопротивление ХС уменьшается, а при  стремится к нулю. Между крайними точками также существует экстремум причем (5.25)Частота, на которой достигается этот максимум определяется выражением  (5.26)Так как подкоренное выражение в (5.24) и (5.26) всегда меньше единицы то очевидно, что  Кроме того 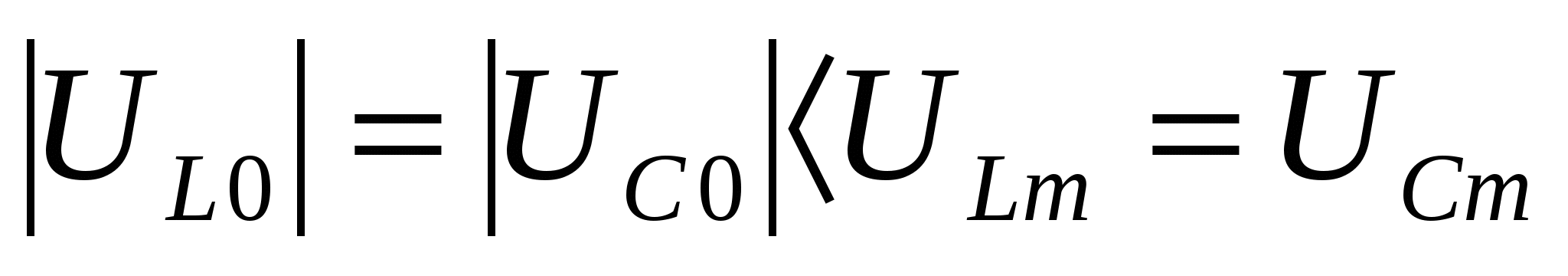 .В силу этих особенностей единственным верным признаком наступления резонанса в цепи является максимум тока, значение которого изменяется с изменением частоты по резонансной кривой. |