Курс лекций по электротехнике часть 1. Лекция элементы электрических цепей
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
Применим к (4.19), (4.11), тогдаКоэффициент называется реактивной мощностью, обозначается Q и измеряется в воль-амперах реактивных [вар]. Теперь общее выражение для мгновенной мощности всей цепи (рис.3.1) можно записать в виде Второе и третье слагаемые в (4.22) свернем как косинус суммы аргументов - Таким образом, мгновенная мощность цепи постоянную и переменную составляющие. Переменная составляющая изменяется относительно постоянной с удвоенной частотой (рис.4.4). Амплитудное значение переменной составляющей обозначают S и называют полной мощностью цепи Полная мощность в 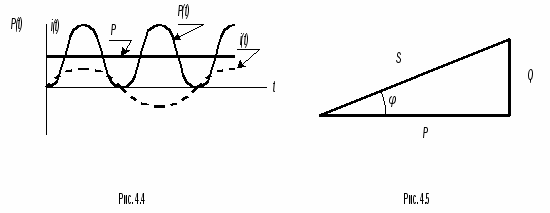 определяется коэффициентом мощности. Физически эта область определяет моменты времени в которые цепь Если умножить все стороны треугольника сопротивлений (рис.3.2) на 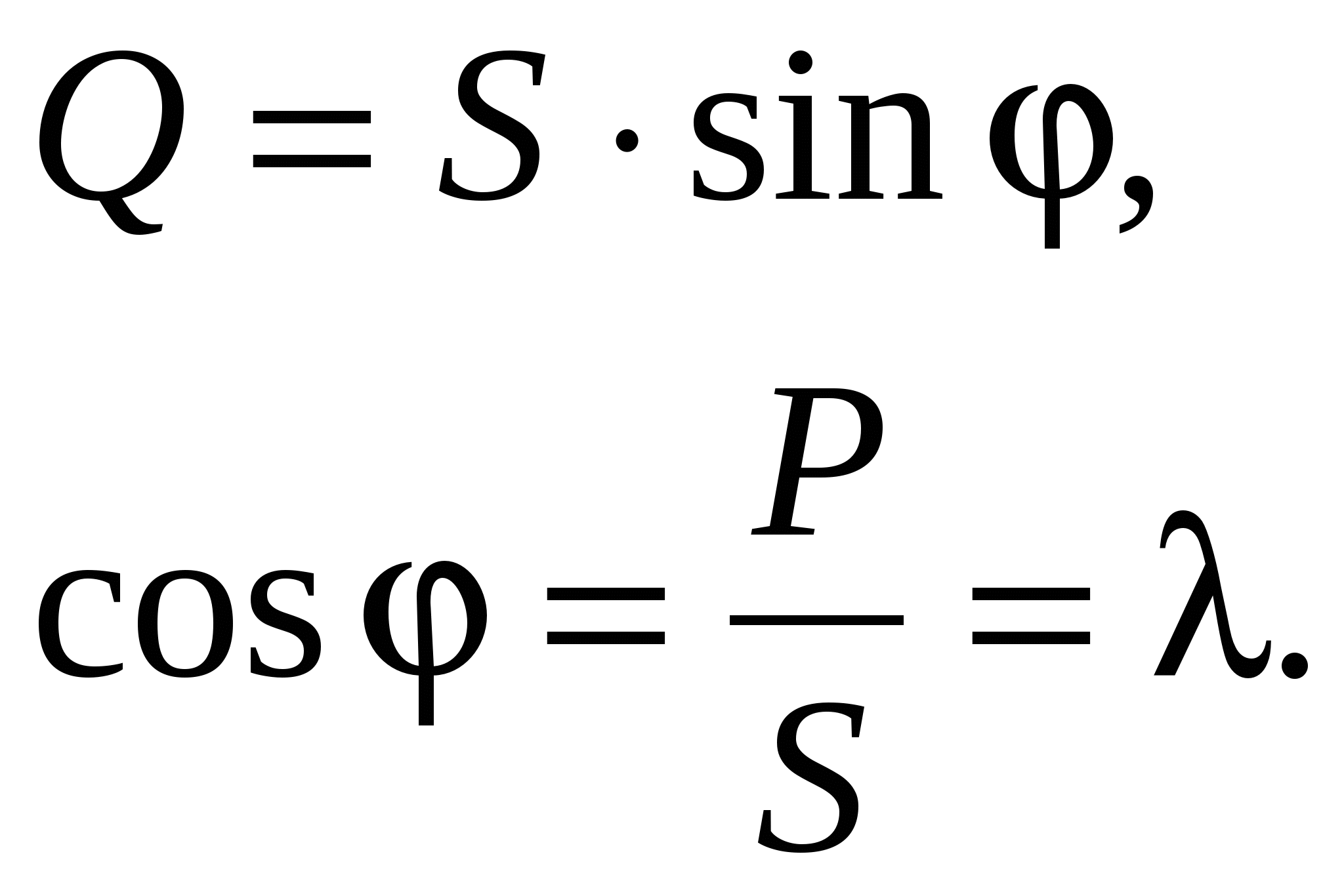 (4.26) (4.26)Полная мощность S это теоретически достижимая, расчетная мощность, По значению S производятся расчеты сечения проводов, изоляция, параметры приемников электрической энергии. Из-за сдвига фаз
Широкое применение комплексного представления тока и напряжения в процессе анализа электрических цепей предполагает найти комплексное представление для активной, реактивной и полной мощности. На первый взгляд эта задача не должна вызывать затруднений. Достаточно в выражение для мощности подставить комплексные ток и напряжение. Посмотрим так ли это? Пусть заданы комплексные ток Тогда их произведение должно представлять полную мощность цепи. Правая часть полученного выражения должна определять активную (действительную часть) и реактивную (мнимая часть) мощности. Но слагаемые правой части не соответствуют выражениям (4.16) и (4.21), так как в них сдвиг фаз определяется разностью Чтобы устранить такое несоответствие пользуются искусственным приемом. Под комплексным изображением полной мощности понимают произведение комплексного напряжения на комплексно-сопряженный ток. Напомним, что два комплексных числа При таком определении комплексная мощность цепи определится выражением Знак «тильда» означает комплекс полной мощности, составленный при участии сопряженного комплекса тока. Действительная часть комплексной мощности есть полная мощность, а мнимая часть - реактивная мощность. Модуль комплексного представления - полная мощность. 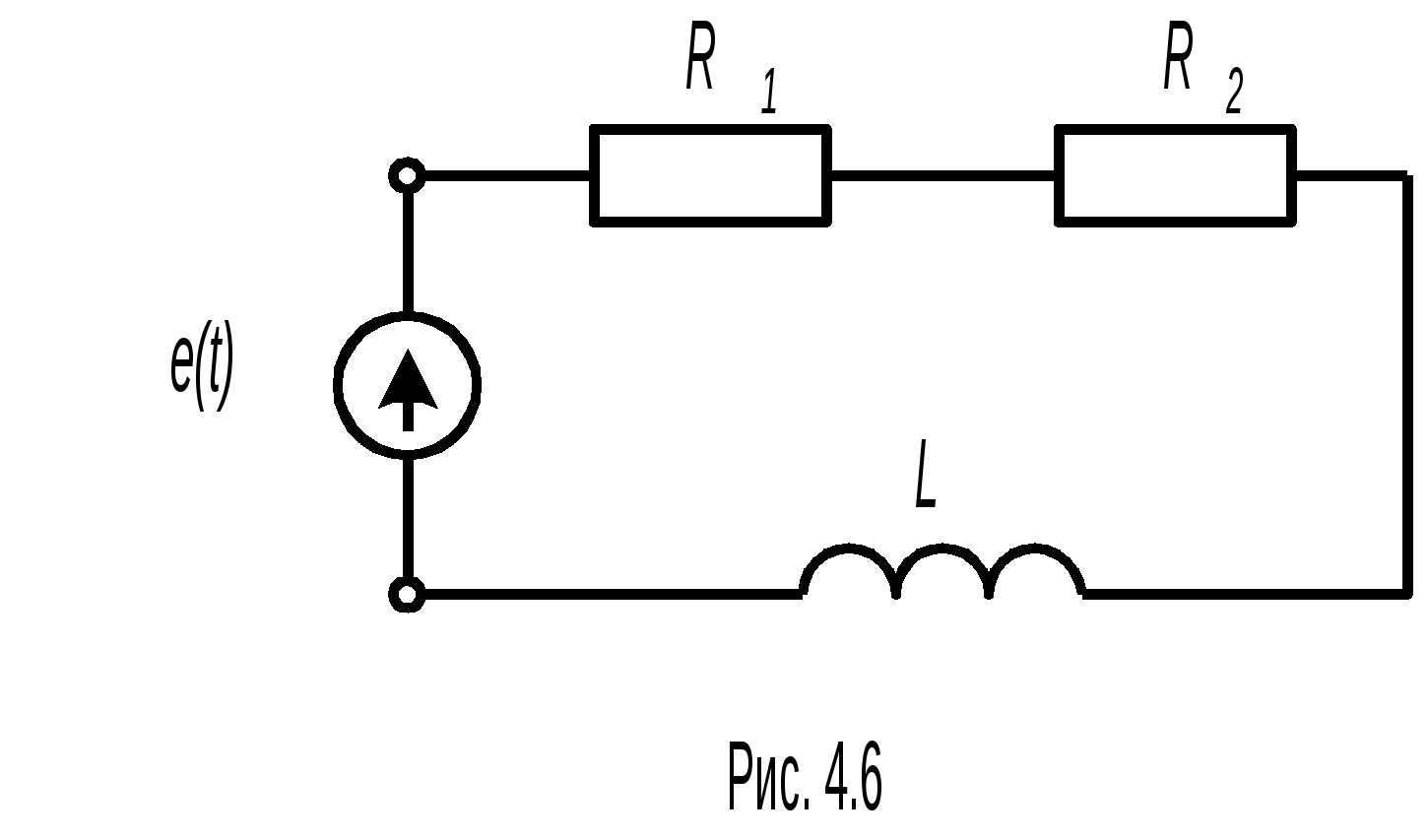 Рассмотрим пример. Пусть в схеме рис. (4.6) заданы ЭДС - Рассмотрим пример. Пусть в схеме рис. (4.6) заданы ЭДС -Решение Комплекс действующего значения напряжения на входе всей схемы равен Комплексное сопротивление цепи Переходим к показательной форме комплексного сопротивления. Для этого находим модуль и фазу Отсюда Комплекс действующего значения тока Сопряженный комплекс тока Комплекс мощности Отсюда: ЛЕКЦИЯ 1.5. РЕЗОНАНСНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА Мы уже знаем, что алгебраическая форма комплексного сопротивления Z имеет действительную R и мнимую jX части Значение действительной и мнимой частей определяются составом и структурой схемы. Для схемы с последовательно включенными R, L, и С элементами реактивное сопротивление Очевидно, что значение слагаемых зависит от частоты При этой частоте реактивное сопротивление равно нулю, а комплексное сопротивление цепи становится активным. Такой режим выделяют особо и называют резонансным. При резонансном режиме работы электрической цепи принимают режим, при котором ее сопротивление является чисто активным. Различают две разновидности резонансных режимов: резонанс токов и резонанс напряжений.
Резонанс токов возникает в цепи с параллельным включением элементов (рис.5.1). Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением 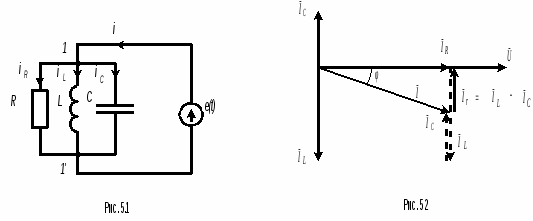 Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа: Применяя к (5.2) выражения (1.7) и (1.12) приведем его к виду Подставим в (5.3) вместо u(t) его значение из (5.1) и решим его Векторная диаграмма, построенная по (5.4) приведена на рис. 5.2. В качестве исходного в ней принят общий для всех элементов цепи вектор напряжения 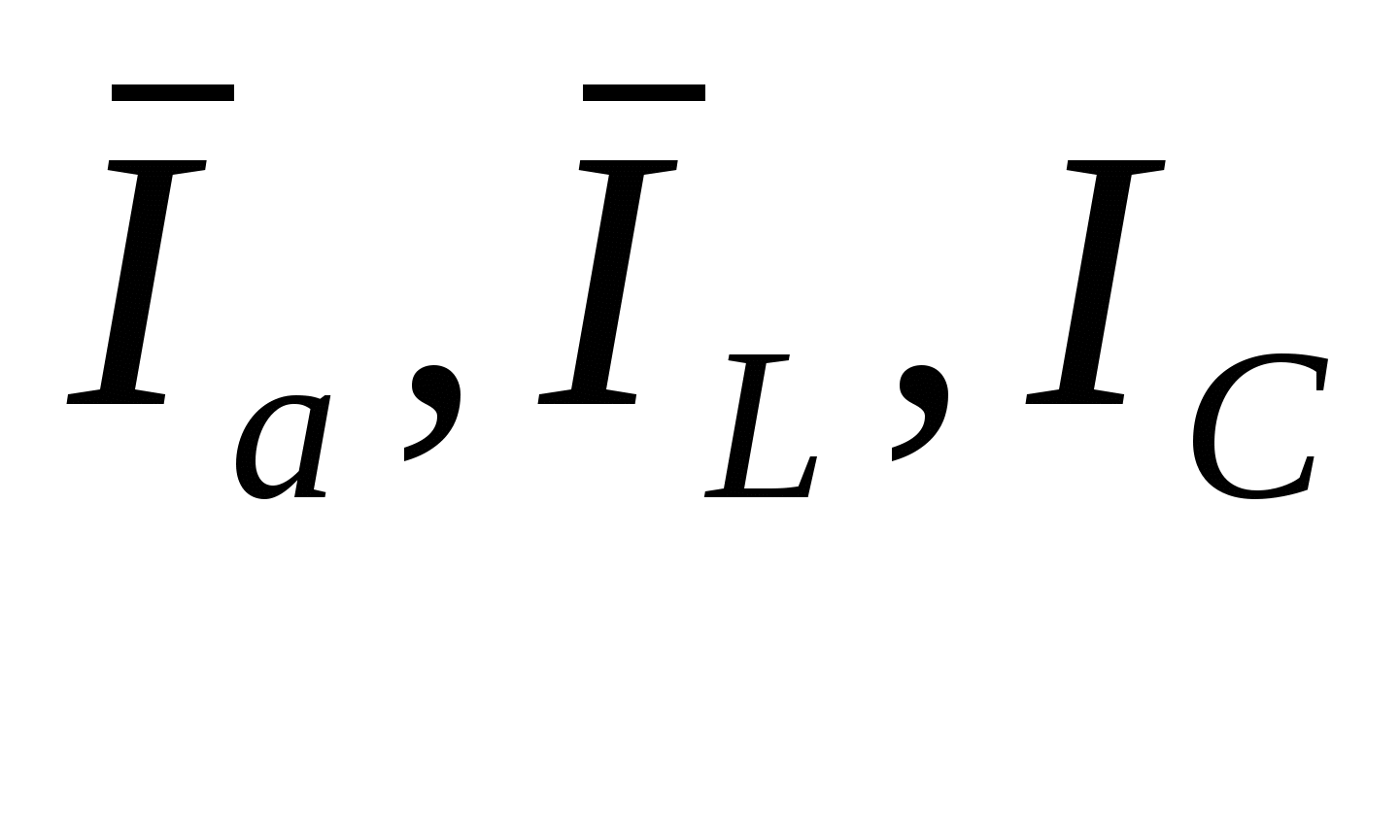 . Результатом сложения является вектор . Результатом сложения является вектор Векторы 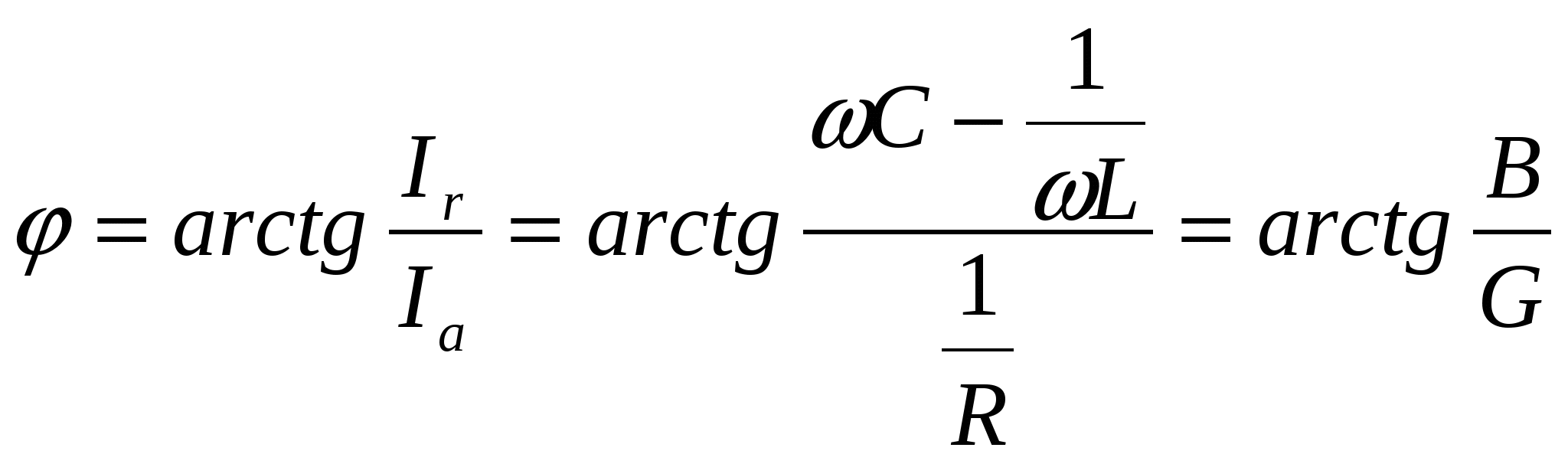 (5.7) (5.7)Треугольник токов наглядно показывает, что для достижения резонанса в цепи необходимо обеспечить равенства противофазных токов Отсюда легко определить: -частоту -значение одного из элементов L или С, если заданы резонансная частота Определим значение тока всей цепи и токов, протекающих в ее ветвях в режиме резонанса. Действующее значение тока всей цепи Но это значение равно току, протекающему через активное сопротивление цепи Ток, протекающий через элемент L определим по закону Ома Подставляя в (5.13) вместо U его значение из (5.11) получим Аналогично определяем выражение для тока через элемент Принимая во внимание (5.8) нетрудно сделать вывод о том, что токи протекающие через индуктивный и емкостной элементы равны по величине, но противоположны по фазе. Величина Q равная может быть больше единицы, в специальных устройствах достигает несколько десятков и сотен единиц и называется добротностью. Еще раз подчеркнем замечательную особенность цепи в режиме резонанса. Токи протекающие в ветвях реактивных элементов могут принимать значения в десятки и сотни раз больше общего тока цепи. Поэтому резонанс цепи называют резонансом токов. Очень важно и то, что они противофазны. Именно это указывает на то, что в цепи происходит колебательный процесс с частотой Чтобы завершить анализ цепи рассмотрим зависимость ее токов и напряжения от частоты (рис.5.4). Ток, протекающий через элемент R - iR определяется законом Ома и не зависит от частоты. Ток через емкость ic согласно (5.15) прямопропорционален частоте, а ток через индуктивность iL -обратнопропорционален. На частоте 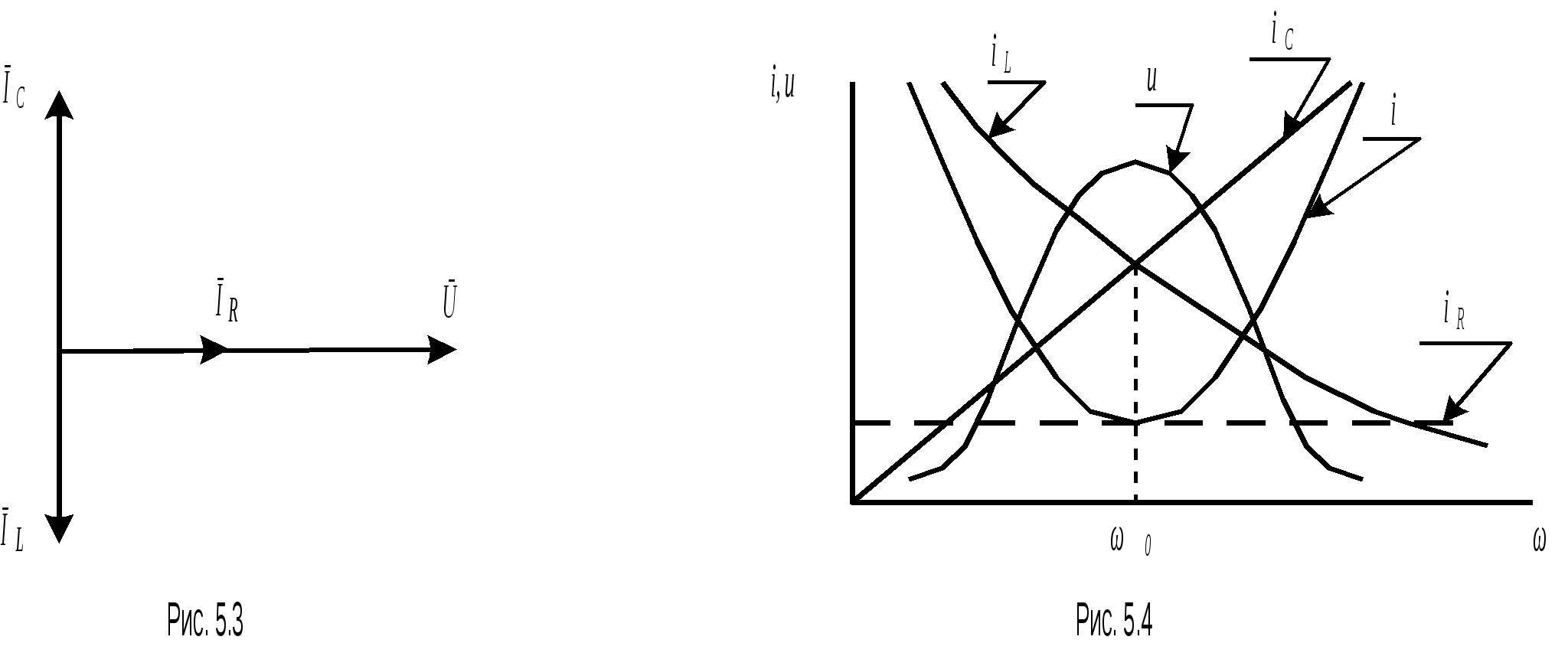
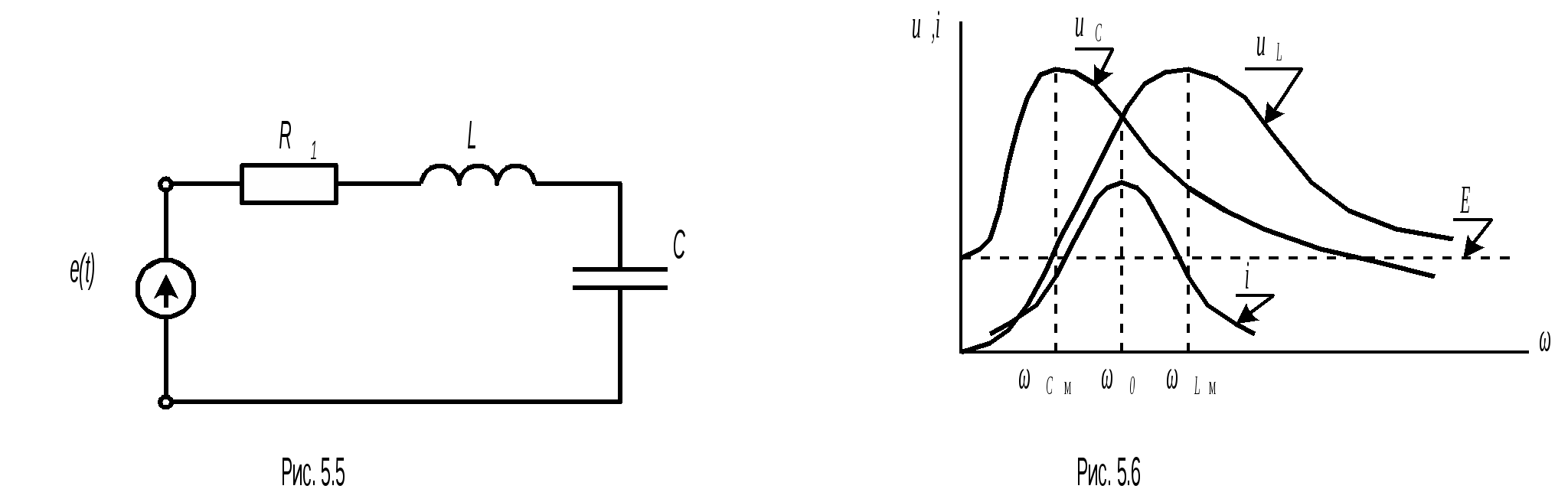 Резонанс напряжений возникает в цепи с последовательным включением элементов (рис.5.5) Известно, что комплексное сопротивление токов цепи определяется выражением. По определению резонанс в цепи рис.5.5 наступает когда выполнится условие Отсюда видно, что резонанс в цепи возникает на частоте |
