кр. Решение Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду Получаем

• Название: Решение Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду Получаем
• Дата: 01.05.2022
• Размер: 51.9 Kb.
• Имя файла: кр.docx
• Тип: Решение; #506422

1. Решить систему уравнений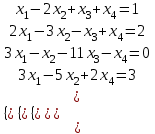

Решение:

Решаем методом Гаусса. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду: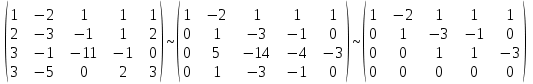



Получаем: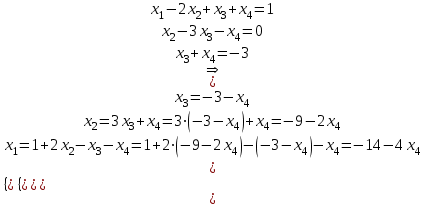



Общее решение системы: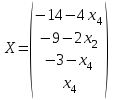

И частное решение: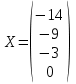
2. Вычислить обратную матрицу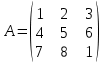

Решение:

Находим определитель матрицы: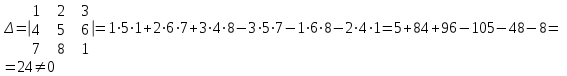



Обратная матрица: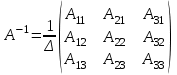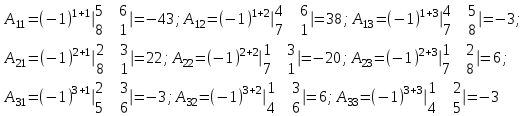



Обратная матрица: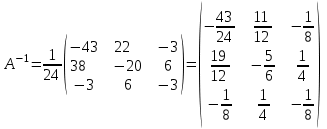

3. Вычислить определитель: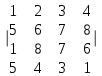

Решение:

Приведем матрицу к ступенчатому виду и вычислим определитель путем перемножения чисел, находящихся на главной диагонали: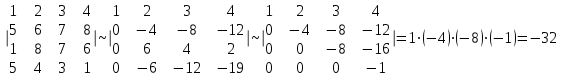


4. Решить задачу линейного программирования симплекс-методом: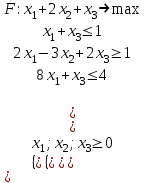



Решение:

Каноническая форма: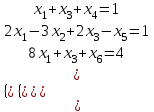

Базис	B	x1	x2	x3	x4	x5	x6	min
x4	1/2	0	3/2	0	1	1/2	0	1/3
x3	1/2	1	-3/2	1	0	-1/2	0	-
x6	7/2	7	3/2	0	0	1/2	1	7/3
F	0	0	-7/2	0	0	-1/2	0	0

Базис	B	x1	x2	x3	x4	x5	x6
x2	1/3	0	1	0	2/3	1/3	0
x3	1	1	0	1	1	0	0
x6	3	7	0	0	-1	0	1
F	7/6	0	0	0	7/3	2/3	0

Оптимальный план можно записать так: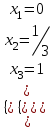

Максимум функции: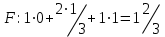
5. Решить матричную игру в смешанных стратегиях за второго игрока, если платежная матрица имеет следующий вид: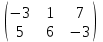



Решение:

Игроки	B1	B2	B3	a = min(Ai)
A1	-3	1	7	-3
A2	5	6	-3	-3
b = max(Bi)	5	6	7

Нижняя цена игры a = max(a_i) = -3, верхняя цена игры b = min(b_j) = 5.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -3 ≤ y ≤ 5.

Находим решение игры в смешанных стратегиях.

Упростим матрицу: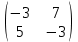

Для игрока 2: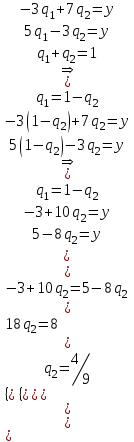



Оптимальная смешанная стратегия игрока 2: .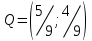

Цена игры: 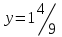.