Лекция 1. Лекция Элементы теории множеств
 Скачать 300.38 Kb. Скачать 300.38 Kb.
|
|
Лекция 1. Элементы теории множеств. 1.1. Множества, подмножества, элементы множества. В отличие от других объектов, изучаемых математикой, термин "множество" не имеет строгого определения. Этот термин употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить (а) о множестве пчёл в улье, (б) о множестве точек отрезка, (в) о множестве вершин квадрата или (г) о множествах его сторон и (д) диагоналей, (е) о множестве студентов в аудитории и т.д. В приведённых примерах в случаях (а), (в)-(е) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример (б)) пересчитать невозможно, такие множества называются бесконечными. Наконец, множество, не содержащее ни одного элемента, называется пустым множеством. Задаются множества различными способами. Наиболее простая форма задания множества - перечисление его элементов, например А={2, 6, 15} (множество А состоит из трёх элементов - целых чисел 2, 6, 15). Другая часто применяемая форма задания - указание свойств элементов множества, например 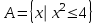 - множество чисел х, удовлетворяющих указанному условию - множество чисел х, удовлетворяющих указанному условию 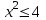 . .Множества обычно обозначаются большими буквами А, В, С,…., а их элементы - малыми: а, в, с,… Запись 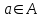 (читается: а принадлежит А) или (читается: а принадлежит А) или 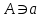 (читается: А содержит а) означает, что а есть элемент множества А. Записи (читается: А содержит а) означает, что а есть элемент множества А. Записи 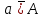 , , 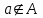 , , 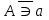 (а не принадлежит А) означает, что а не является элементом множества А. Пустое множество обозначается значком Ø. (а не принадлежит А) означает, что а не является элементом множества А. Пустое множество обозначается значком Ø.Опр.1.1.1. Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - 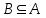 или или 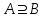 ). ). Согласно этому определению, каждое множество является своим подмножеством (это самое "широкое" подмножество множества). Пустое множество является подмножеством любого множества (это самое "узкое" подмножество). Любое другое подмножество множества А содержит хотя бы один элемент множества А,но не все его элементы. Такие подмножества называются истинными, или собственными подмножествами. Для истинных подмножеств множества А применяется обозначение 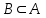 или или 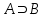 . Если одновременно . Если одновременно 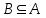 и и 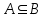 , т.е. каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств =: A=B. (Символы , т.е. каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств =: A=B. (Символы 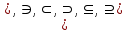 называются символами включения). называются символами включения). Общепринятые обозначения множеств: N = { 1, 2, 3, …} - множество натуральных чисел; Z = {… ,- 4, -3 -2, - 1, 0, 1, 2, 3, ….} - множество целых чисел; Q = 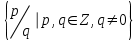 - множество рациональных чисел. - множество рациональных чисел.R - множество вещественных чисел. Рассмотрим простой пример. Пусть А, В, С - подмножества множества N: А={1, 2, 6, 18}; В={6, 1, 18}; С={2, 18, 6, 1},. В этом случае А = С; 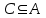 и и 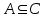 , , 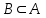 . .Геометрически множества обычно изображаются как некоторые множества точек плоскости. В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Так, на рис. 1 изображено универсальное множество Uи два его подмножества - множества А и В, 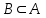 . Сами картинки типа рис. 1 называются диаграммами Эйлера-Венна. . Сами картинки типа рис. 1 называются диаграммами Эйлера-Венна. 1.2. Операции над множествами. В этом параграфе будут рассмотрены три простые операции, которые можно производить над множествами: объединение, пересечение и разность (дополнение) множеств. Опр.1.2.1. Пусть даны множества А и В. Их объединением называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В. Объединение множеств обозначается символами "+" и " 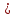 ": ": 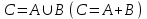 . Пусть, например, А={-6, -3, 0, 3, 6} B={0, 2, 4, 6, 8}. Тогда . Пусть, например, А={-6, -3, 0, 3, 6} B={0, 2, 4, 6, 8}. Тогда 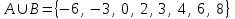 . Геометрически объединение множеств изображено на рис. 2. . Геометрически объединение множеств изображено на рис. 2.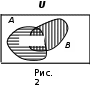 Аналогично определяется объединение большего числа множеств. Опр.1.2.2. Объединением множеств А1, А2, А3, …, Аn (обозначение 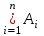 называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А1, А2, А3, …, Аn. называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А1, А2, А3, …, Аn.Свойства операции объединения. Теор. 1.2.1. Справедливы следующие равенства: 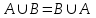 (коммутативность); (коммутативность);(А 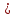 В) В)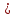 С=А С=А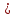 (В (В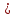 С) (ассоциативность); С) (ассоциативность);Если 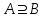 , то А , то А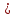 В= А; В= А;А 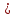 Ø= А. Ø= А.Док-во. Формулы, подобные формулам 1-2, обычно доказываются так. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части. В результате для формулы 1, например, будет доказано, что 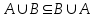 . Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что . Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что 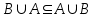 . Из включений . Из включений 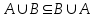 и и 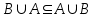 следует, что следует, что 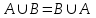 . .Итак, пусть 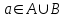 . Это значит, что либо . Это значит, что либо 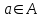 , либо , либо 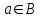 , либо одновременно , либо одновременно 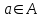 и и 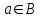 . Во всех трех случаях . Во всех трех случаях 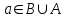 . Включение . Включение 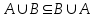 доказано. Пусть теперь доказано. Пусть теперь 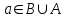 . Это значит, что либо . Это значит, что либо 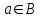 , либо , либо 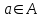 , либо одновременно , либо одновременно 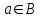 и и 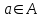 . Во всех трех случаях . Во всех трех случаях 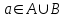 . Включение . Включение 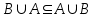 доказано. Следовательно, доказано. Следовательно, 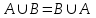 , что и требовалось доказать. , что и требовалось доказать.Другой способ доказательства - изобразить левую и правую часть равенства для одних и тех же множеств на диаграммах Эйлера-Венна и убедиться, что они изображают одно и тоже множество. Так, для формулы 1 диаграммы приведены ниже.  Задание. Самостоятельно доказать включения соответствующих множеств и изобразить диаграммы для формул 2-4. Опр.1.2.3. Пересечением множеств А и В называется множество С, состоящее из элементов, принадлежащих одновременно и множеству А, и множеству В. Если множества А и В не имеют общих элементов, их пересечение равно пустому множеству; в этом случае множества А и В называются непересекающимися. 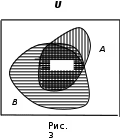 Пересечение множеств обозначается символами " Пересечение множеств обозначается символами "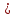 " и " " и "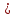 " (знак умножения): " (знак умножения): 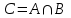 или С=АВ. Для примера, приведенного после опр.1.2.1, или С=АВ. Для примера, приведенного после опр.1.2.1, 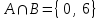 . Геометрически пересечение множеств представлено на рис. 3. . Геометрически пересечение множеств представлено на рис. 3.Свойства операции пересечения множеств. Теор. 1.2.2. Справедливы следующие равенства: 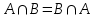 (коммутативность); (коммутативность);(А 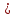 В) В) 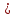 С=А С=А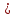 (В (В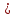 С) (ассоциативность); С) (ассоциативность);Если 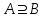 , то А , то А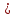 В= В; В= В;А 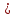 Ø=Ø. Ø=Ø.Задание. Самостоятельно доказать включения соответствующих множеств и изобразить диаграммы для формул 5-8. Опр. 1.2.4 пересечения множеств для большего числа множеств: Пересечением множеств А1, А2, А3, …, Аn (обозначение 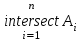 ) называется множество, состоящее из элементов, входящих в каждое из множеств А1, А2, А3, …, Аn. ) называется множество, состоящее из элементов, входящих в каждое из множеств А1, А2, А3, …, Аn.Теор. 1.2.3. Для операций объединения и пересечения множеств справедливы законы дистрибутивности: 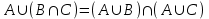 ; ;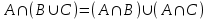 . .Док-во: Докажем формулу 9. Пусть 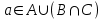 . Тогда либо . Тогда либо 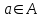 (следовательно, (следовательно, 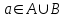 и и 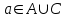 , т.е. , т.е. 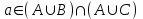 ); либо ); либо 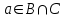 (следовательно, одновременно, (следовательно, одновременно, 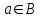 ( (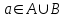 ) и ) и 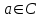 ( (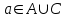 ), т.е. ), т.е. 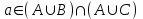 ); либо одновременно ); либо одновременно 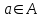 и и 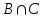 (в этом случае можно применить любое из приведённых выше рассуждений). Таким образом, доказано, что (в этом случае можно применить любое из приведённых выше рассуждений). Таким образом, доказано, что 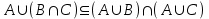 . .Пусть 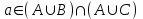 . Рассмотрим два случая. 1. Пусть . Рассмотрим два случая. 1. Пусть 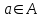 .Тогда .Тогда 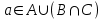 . 2. Пусть . 2. Пусть 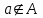 , но , но 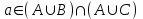 , т.е. одновременно и , т.е. одновременно и 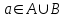 , и , и 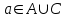 . Это возможно, только если одновременно и . Это возможно, только если одновременно и 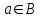 , и , и 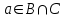 , откуда следует, что , откуда следует, что 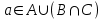 . Включение . Включение 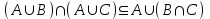 доказано. доказано. Задание. Самостоятельно доказать формулу 10. Опр. 1.2.5. Разностью множеств А и В называется множество А\В, содержащее те элементы множества А, которые не принадлежат множеству В. 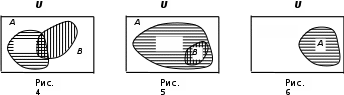 В опр. 1.2.5 не предполагается, что 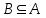 (рис. 4). Если же (рис. 4). Если же 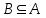 , то разность А\В называется дополнением множества В до множества А(рис. 5). Для дополнения множества А до универсального множества Uприменяется обозначение , то разность А\В называется дополнением множества В до множества А(рис. 5). Для дополнения множества А до универсального множества Uприменяется обозначение 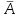 (рис. 6). (рис. 6).Теор. 1.2.4. Операции разности и дополнения антидистрибутивны относительно операций объединения и пересечения: 11. 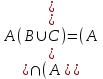 ; ;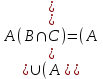 . .(Дополнение к объединению некоторых множеств равно пересечению их дополнений; дополнение к пересечению множеств равно объединению их дополнений. Другими словами, символ дополнения \ можно менять местами со знаками 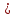 и и 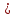 , при этом один из этих знаков заменяется другим). , при этом один из этих знаков заменяется другим).Док-во. Докажем формулу 11. Пусть 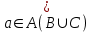 . Это означает, что . Это означает, что 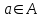 и и 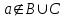 , т.е. , т.е. 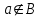 , , 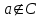 . Следовательно, . Следовательно, 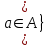 и и 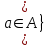 , т.е. , т.е. 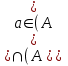 . Включение . Включение 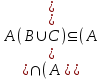 доказано. доказано.Пусть 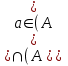 . Это означает, что одновременно и . Это означает, что одновременно и 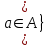 (т.е. (т.е. 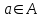 и и 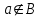 ), и ), и 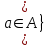 (т.е. (т.е. 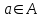 и и 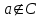 ). Так как ). Так как 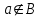 и и 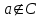 , то , то 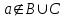 . Но . Но 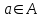 , следовательно, , следовательно, 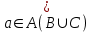 . Включение . Включение 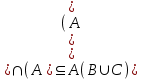 доказано. Из справедливости доказанных включений следует справедливость формулы 11. доказано. Из справедливости доказанных включений следует справедливость формулы 11. Задание. Самостоятельно доказать формулу 12 и обобщение формул 11, 12 на большее число множеств: 13. 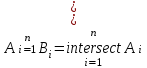 ; 14. ; 14. 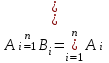 . .2. Действительные числа. 2.1. Аксиомы действительных чисел. Множество R={x,y,z,…} действительных чисел - множество мощности континуум, на котором определены две операции (сложение и умножение) и отношение упорядоченности ( 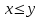 ), удовлетворяющие аксиомам ), удовлетворяющие аксиомам I.1. x+y=y+x; I.2. (x+y)+z= x+(y+z); I.3. Существует такой элемент 0R, что 0+х=х для хR; I.4. Для каждого элемента хR существует такой элемент - х, что х+(- х)=0; II.1.xy=yx; II.2. (xy)z=x(yz); II.3. Существует такой элемент 1R, что 1х=х для хR; II.4. Для каждого элемента х0, х R существует такой элемент х-1R, что х х-1=1; III.1. x(y+z)=xy+xz; IV.1. Отношение {( 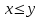 )( y x)} эквивалентно отношению х=у; )( y x)} эквивалентно отношению х=у;IV.2. Для любых двух элементов хR, уR или ху, или ух; IV.3. Из 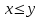 и yzследует хz; и yzследует хz;IV.4. Из ху следует х+z у+zдля любых х,у,z R; IV.5. Из 0 х и 0 у следует 0 ху. Отношение 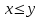 записывается также в форме ух. Отношение {( записывается также в форме ух. Отношение {(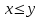 )( xy)} записывается в форме х<у. )( xy)} записывается в форме х<у. V. Аксиома непрерывности: для любых элементов хR, уR таких, что х < у, существует элементz R, такой что х<z < у. VI. Аксиома Архимеда: для любых элементов хR, уR таких, что 0<х, 0<у, существует такое натуральное число n, что уnх; VII. Аксиома о вложенных отрезках: если {[an, bn]} - счётная последовательность отрезков, таких что anan+1 и bn+1bn при n, то пересечение этой последовательности непусто, т.е. хR: х[an, bn] для n. 2.2. Некоторые множества на числовой оси. Определения. 2.2.1. Для любой пары элементов aR, bR такой, что a<b, множество действительных чисел х, удовлетворяющей условию а<х<b, называется открытым промежутком, или интервалом с началом а и концом b и обозначается (a,b) (или ]a ,b[). 2.2.2. Множество действительных чисел х, удовлетворяющей условию ахb, называется замкнутым промежутком, или отрезком и обозначается [a,b] 2.2.3. Определения полуоткрытых промежутков: (a,b]={x| а<хb}; [a,b)={x| ах<b}. 2.2.4. Пусть R, >0. -окрестностью числа (точки) х0 называется множество. 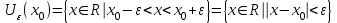 . .2.2.5. Проколотой -окрестностью числа (точки) х0 называется множество 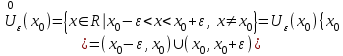 . .Пусть Х – произвольное множество действительных чисел. 2.2.6. Точка х0 называется предельной точкой множества Х, если в любой -окрестности точки х0 имеются элементы множества Х, отличные от х0. Предельная точка множества может принадлежать этому множеству, а может не принадлежать ему. Так, точка х0 = 1 является предельной и для отрезка [0, 1], и для интервала (0, 1). 2.3. Несобственные точки числовой прямой. Дополним множество вещественных чисел тремя новыми объектами (-, +, ), которые определим через систему их окрестностей. Определения. 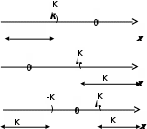 2.3.1. Несобственной точкой - будем называть объект, К-окрестность которого - множество 2.3.1. Несобственной точкой - будем называть объект, К-окрестность которого - множество 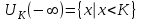 . .Для уR выполняется -<у. 2.3.2. Несобственной точкой + будем называть объект, К-окрестность которого - множество 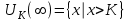 . .Для уR выполняется у<+. 2.3.3. Пусть К>0. Несобственной точкой будем называть объект, К-окрестность которого - множество 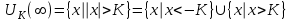 . .2.4. Границы числовых множеств. Пусть Х={x|xR} - некоторое подмножество множества действительных чисел. Определения. 2.4.1. Если существует число МR такое, что для хХ выполняется неравенство х<М, то множество Х называется ограниченным сверху (числом М). Число М называется верхней границей множества Х. 2.4.2. Если существует число mR такое, что для хХ выполняется неравенство х>m, то множество Х называется ограниченным снизу (числом m). Число m называется нижней границей множества Х. 2.4.3. Если существует число МR такое, что для хХ выполняется неравенство |х|<М, то множество Х называется ограниченным. Теорема 2.4.1. Множество ограничено тогда и только тогда, когда оно ограничено сверху и снизу. Если множество Х ограничено сверху, то множество его верхних границ бесконечно (если число М - верхняя граница, то верхними границами будут числа М+1, М+2 и т.д.). Обозначим У множество верхних границ множества Х. Множество У ограничено снизу (любым элементом множества Х). Возможны два случая: либо множество Х имеет максимальный элемент (например, если Х – отрезок [0, 1], то максимальный элемент равен 1), в этом случае множество верхних границ не имеет минимального элемента; либо множество Х не имеет максимального элемента (например, если Х = (0, 1)), в этом случае множество верхних границ имеет минимальный элемент. Определение 2.4.4. Точной верхней границей, или верхней гранью, множества Х, ограниченного сверху, называется максимальный элемент этого множества, если он существует, и минимальный элемент множества верхних границ, если множество Х не имеет максимального элемента. Для обозначения применяются: символы sup X или sup{x}. Свойства верхней грани: Пусть М*= sup X - верхняя грань множества Х. Тогда 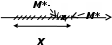 2.4.2. Для хХ выполняется неравенство х М*. 2.4.2. Для хХ выполняется неравенство х М*.2.4.3. Любое число, меньшее М*, не будет верхней границей множества Х, т.е. для >0 xX такой, что х> М*-. Аналогичным образом, если множество Х ограничено снизу, то множество его нижних границ бесконечно. Обозначим Z множество нижних границ множества Х. Множество Z ограничено сверху (любым элементом множества Х). Определение 2.4.5. Точной нижней границей, или нижней гранью, множества Х, ограниченного снизу, называется минимальный элемент этого множества, если он существует, и максимальный элемент множества нижних границ, если множество Х не имеет минимального элемента. Для обозначения применяются: символы inf X или inf{x}. Свойства нижней грани: Пусть М*= inf X - нижняя грань множества Х. Тогда 2.4.2. Для хХ выполняется неравенство х М*. 2.4.3. Любое число, большее М*, не будет нижней границей множества Х, т.е. для >0 xX такой, что х М*+. Основная литература 1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Физматлит, 2006. Т. 1 – 2 2. Кудрявцев Л.Д. Курс математического анализа. Т. 1, Т .2 3. Сборник задач по высшей математике. 1 курс / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко . – 7-е изд. – М.: Айрис-пресс, 2008 – 576 с. 4. Г.Н. Берман. Сборник задач по курсу математического анализа. М., Наука. 5. Аксенов, А.П. Математический анализ в 4 ч. части 1, 2, 3,4. Учебник и практикум для академического бакалавриата / А.П. Аксенов. - Люберцы: Юрайт, 2016. |
