Лекция 1. Кубические сплайны. Лекция Кубические сплайны
 Скачать 179.53 Kb. Скачать 179.53 Kb.
|
Лекция 1. Кубические сплайныРассмотрим задачу проведения гладких кривых по заданным граничным точкам, или задачу интерполяции. Поскольку через две точки можно провести сколь угодно много гладких кривых, то для решения этой задачи необходимо ограничить класс функций, которые будут определять искомую кривую. Математическими сплайнами называют функции, используемые для аппроксимации кривых. Важным их свойством является простота вычислений. На практике часто используют сплайны вида полиномов третьей степени. С их помощью довольно удобно проводить кривые, которые интуитивно соответствуют человеческому субъективному понятию гладкости. Термин “сплайн” происходит от английского spline – что означает гибкую полоску стали, которую применяли чертежники для проведения плавных кривых, например, для построения обводов кораблей или самолетов. Рассмотрим в начале сплайновую функцию для построения графика функции одной переменной. Пусть на плоскости задана последовательность точек 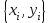 , ,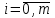 , причем , причем 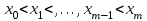 . Определим искомую функцию . Определим искомую функцию 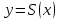 , причем поставим два условия: , причем поставим два условия:Функция должна проходить через все заданные точки: 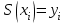 , , 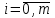 . .Функция должна быть дважды непрерывно дифференцируема, то есть иметь непрерывную вторую производную на всем отрезке 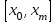 . .На каждом из отрезков 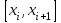 , , 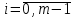 будем искать нашу функцию в виде полинома третьей степени: будем искать нашу функцию в виде полинома третьей степени: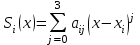 . .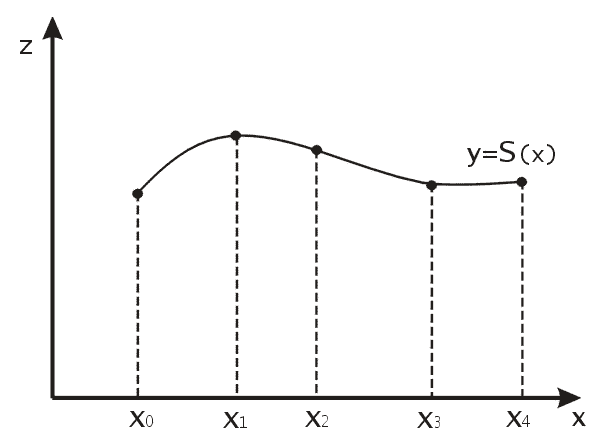 Рис. 40. Сплайновая функция. Задача построения полинома сводится к нахождению коэффициентов 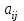 . Поскольку для каждого из отрезков . Поскольку для каждого из отрезков 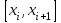 необходимо найти 4 коэффициента необходимо найти 4 коэффициента 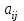 , то всего количество искомых коэффициентов будет , то всего количество искомых коэффициентов будет 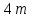 . Для нахождения всех коэффициентов определим соответствующее количество уравнений. Первые . Для нахождения всех коэффициентов определим соответствующее количество уравнений. Первые 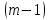 уравнений получаем из условий совпадения значений функции во внутренних узлах уравнений получаем из условий совпадения значений функции во внутренних узлах 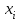 , ,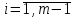 . Следующие . Следующие 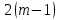 уравнений получаем аналогично из условий совпадения значений первых и вторых производных во внутренних узлах. Вместе с первым условием получаем уравнений получаем аналогично из условий совпадения значений первых и вторых производных во внутренних узлах. Вместе с первым условием получаем 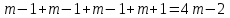 уравнений. Недостающие два уравнения можно получить заданием значений первых производных в концевых точках отрезка уравнений. Недостающие два уравнения можно получить заданием значений первых производных в концевых точках отрезка 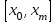 . Так могут быть заданы граничные условия. . Так могут быть заданы граничные условия.Перейдем к более сложному случаю – заданию кривых в трехмерном пространстве. В случае функционального задания кривой 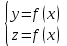 возможны многозначности в случае самопересечений и неудобства при значениях производных равных возможны многозначности в случае самопересечений и неудобства при значениях производных равных 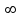 . Ввиду этого будем искать функцию в параметрическом виде. Пусть . Ввиду этого будем искать функцию в параметрическом виде. Пусть 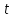 - независимый параметр, такой что - независимый параметр, такой что 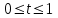 . Кубическим параметрическим сплайном назовем следующую систему уравнений: . Кубическим параметрическим сплайном назовем следующую систему уравнений: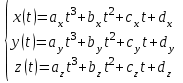 Координаты точек на кривой описываются вектором 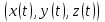 , а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты , а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты 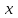 : :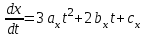 . .Одним из способов задания параметрического кубического сплайна является указание координат начальной и конечной точек, а также векторов касательных в них. Такой способ задания называется формой Эрмита. Обозначим концевые точки 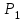 и и 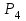 , а касательные векторы в них , а касательные векторы в них 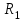 и и 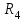 . Индексы выбраны таким образом с учетом дальнейшего изложения. . Индексы выбраны таким образом с учетом дальнейшего изложения. Будем решать задачу нахождения четверки коэффициентов 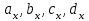 , так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна: , так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна: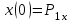 , , 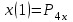 , , 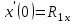 , , 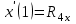 (*) (*)Перепишем выражение для 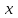 в векторном виде: в векторном виде: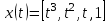 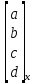 . .Обозначим вектор строку 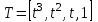 и вектор столбец коэффициентов и вектор столбец коэффициентов 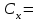 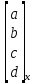 , тогда , тогда 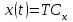 . .Из (*) следует, что 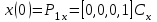 , , 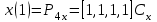 . Для касательных . Для касательных 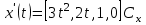 , ,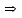 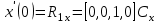 , , 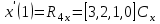 . Отсюда получаем векторно-матричное уравнение: . Отсюда получаем векторно-матричное уравнение: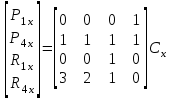 . . Эта система решается относительно 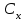 нахождением обратной матрицы размером нахождением обратной матрицы размером 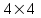 . .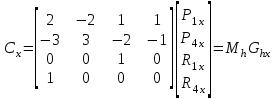 . .Здесь 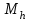 - эрмитова матрица, - эрмитова матрица, 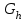 - геометрический вектор Эрмита. Подставим выражение - геометрический вектор Эрмита. Подставим выражение 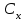 для нахождения для нахождения 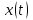 : : 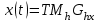 . Аналогично для остальных координат: . Аналогично для остальных координат: 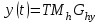 , , 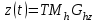 . .Выпишем в явном виде формулы для вычисления координат точек сплайна. Так как 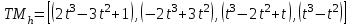 , то умножая справа на , то умножая справа на 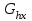 , получаем: , получаем: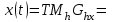 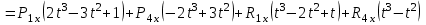 . .Четыре функции в скобках называются функциями сопряжения. Форму кривой, заданной в форме Эрмита, легко изменять если учитывать, что направление вектора касательной задает начальное направление, а модуль вектора касательной задает степень вытянутости кривой в направлении этого вектора, как показано на рис. 41.  Рис. 41. Параметрический сплайн в форме Эрмита. Вытянутость кривой вправо обеспечивается тем, что 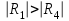 . .Рассмотрим форму Безье, которая отличается от формы Эрмита способом задания граничных условий, а именно, вместо векторов 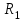 и и 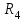 вводятся точки (и соответствующие им радиус векторы) вводятся точки (и соответствующие им радиус векторы) 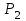 и и 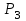 , как показано на рис.42, такие что выполняются условия: , как показано на рис.42, такие что выполняются условия: 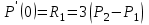 и и 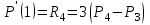 . .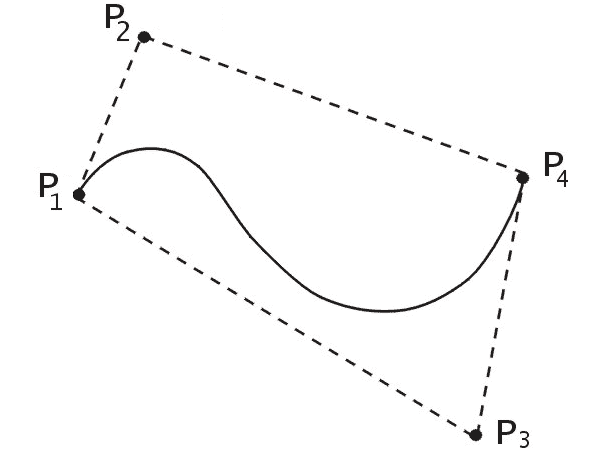 Рис. 42. Параметрический сплайн в форме Безье. Переход от формы Эрмита к форме Безье осуществляется преобразованием: 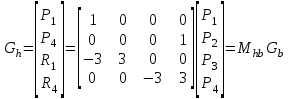 , (*) , (*)где 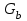 - геометрический вектор Безье. Подставляя это в выражение для - геометрический вектор Безье. Подставляя это в выражение для 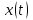 , получаем , получаем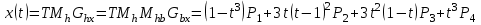 . .Полезным свойством сплайнов в форме Безье является то что кривая всегда лежит внутри выпуклой оболочки, образованной четырехугольником 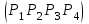 . Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице. . Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице.Заметим, что матрица вида 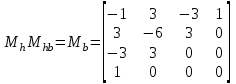 - называется матрицей Безье. - называется матрицей Безье.Методические указания к ЛАБОРАТОРНОЙ РАБОТЕ №1«Построение Сплайновых кривых»по дисциплине «КОМПЬЮТЕРНАЯ ГРАФИКА»Цель работы: изучение способов описания элементарных сплайновых кривых и получение практических навыков построения составных и рациональных сплайновых кривых. 1. Теоретические положения По заданному множеству вершин 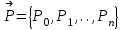 с учетом их нумерации необходимо построить гладкую кривую, которая, плавно меняясь, последовательно проходила бы в близости этих вершин и удовлетворяла бы некоторым дополнительным условиям. с учетом их нумерации необходимо построить гладкую кривую, которая, плавно меняясь, последовательно проходила бы в близости этих вершин и удовлетворяла бы некоторым дополнительным условиям. При отыскании подходящего решения задачи приближения важную роль играет ломанная, звенья которой последовательно соединяют рассматриваемые вершины заданного набора. Эту ломанную называют контрольной, а ее вершины – контрольными. Ограничение на множество вершин не накладывается: вершины могут располагаться как на плоскости, так и в пространстве, их взаимное расположение может быть произвольным; некоторые вершины могут и совпадать. Поэтому описание кривой ищется в параметрическом виде: 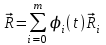 , ,где 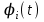 - весовая функция - весовая функцияДля решения задачи приближения успешно применяются кривые, составленные из элементарных фрагментов. В случае, когда элементарные фрагменты строятся по сравнительно простой схеме, такие составные кривые принято называть сплайновыми кривыми. Наибольшее распространение получили методы конструирования составных кривых, в которых используются кубические многочлены, что позволяет учесть и дифференциальные и внешне геометрические требования, накладываемые на искомую кривую. На рисунке 3.1. приведены способы задания четырех векторов для определения элементарной кубической кривой. 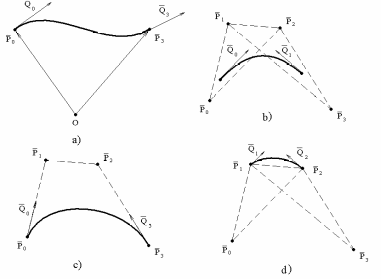 Рис. 3.1. а) элементарная кривая Эрмита, b) элементарный В-сплайн, с) элементарная кривая Безье, d) элементарная кривая Catmull-Rom. Элементарная кубическая кривая Безье описывается уравнением вида: 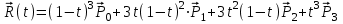 Элементарная В–сплайновая кривая описывается уравнением вида: 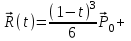 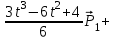 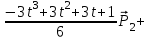 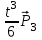 Элементарная кривая Эрмита описывается уравнением вида: 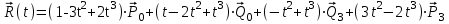 Элементарная кривая Catmull-Rom описывается уравнение вида: 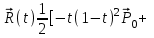 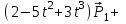 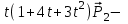 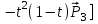 Построив кривую, ее можно подвергнуть аффинному преобразованию. Можно поступить по другому: сначала подвергнуть преобразованию заданный набор опорных вершин, только потом построить кривую. Если результат окажется одинаковым, то говорят, что кривая инвариантна относительно этого преобразования. Большинство из рассматриваемых классов кривых обладает свойством аффинной инвариантности. Рассматривая составную кривую у как целое, более естественно пользоваться единой параметризацией. Наиболее простой является параметризация с равноотстоящими целочисленными узлами. Для массива из nопорных вершин составная кубическая эрмитова кривая строится из n+1 элементарных фрагментов. В этом случае узлы параметризации определяются по формуле 2. Задание на работу. Написать програму в MS Visual C++ для построения кубических сплайновых кривых: Эрмита, В-сплайн, Безье, Catmull-Rom по заданному массиву точек с учетом их нумерации. Заданный массив точек:
Отчет должен содержать: цель работы, задание на работу, текст отлаженной программы, результаты работы программы. |
