Лекция 5.1. Лекция Основные сведения о климатических и механических факторах, воздействующих на рэа

• Название: Лекция Основные сведения о климатических и механических факторах, воздействующих на рэа
• Дата: 28.10.2020
• Размер: 0.66 Mb.
• Имя файла: Лекция 5.1.docx
• Тип: Лекция; #146407

Лекция

Основные сведения о климатических и механических факторах, воздействующих на РЭА
Для разработки технических условий, а так же для составления программы и методики испытаний не­обходимо знание климатических условий эксплуатации и механических воздействий, которым подвергается РЭА.

Климатические условия (климат) определяются ре­жимами погоды, в разных частях земной поверхности за продолжительный период времени. Основными показате­лями, характеризующими режим погоды, являются: тем­пература, атмосферное давление, влажность, господст­вующие ветры и осадки.

Формирование климата на определенной территории обусловливают следующие климатообразующие факто­ры: радиационный режим, циркуляция атмосферы, влагооборот и местные физико-географические особенности (характер подстилающей поверхности, под которым по­нимается верхний слой почвы, растительный покров, верхний слой воды, снежный покров, ледяной покров и т. п.). Перечисленные факторы определяют тепловой и водный баланс поверхности Земли в природной геогра­фической среде.

Радиационный режим характеризуется распре­делением радиационного баланса, учитывающего при­ход-расход энергии солнечной радиации. Составными частями радиационного баланса являются прямая (Q) и рассеянная (q) солнечная радиация, а также эффективное излучение Земли (Е), под которым понимают разность между двумя потоками: одного - направленно­го от земной поверхности к атмосфере, другого - проти­воизлучения от атмосферы к земной поверхности. Для характеристики отношения отраженной энергии к падаю­щей пользуются числом, носящим название альбедо (а). Часто альбедо выражают в процентах. Очевидно, что отражение энергии зависит от местных физико-геогра­фических условий земной поверхности, включая близость моря, высоту места, направление горных хребтов, мор­ских течений и т. д. Радиационный баланс выражается следующим уравнением:

R=(Q + q)(l-a)-E. (1)

Величину солнечной радиации оценивают числом ка­лорий тепла, приносимого солнечными лучами в едини­цу времени на 1 см2 поверхности. Количество калорий тепла, приносимых солнечными лучами за 1 минуту на 1 см2 поверхности, при условии, что исключается ослаб­ляющее действие воздуха, принято называть солнечной постоянной. Оно примерно составляет 2 кал/см2 • мин.

На основании многочисленных исследований .радиа­ционных условий отдельных пунктов Земли разработа­ны мировые карты составляющих радиационного балан­са и установлено, что среднемесячные суточные значе­ния суммарной солнечной радиации при безоблачном небе (Q­­0) являются сравнительно устойчивыми величи­нами и в основном определяются широтой места и вре­менем года (рис. 1).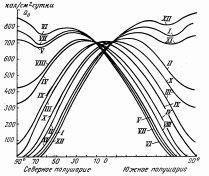



Рис. 1.1 Среднемесячные суточные значения суммарной солнечной радиации при безоблачном небе в зависимости от широты места и времени года
Суточный ход и часовые суммы солнечной радиации зависят от места расположения климатической области и характерных для нее погодных условий (рис. 1.2). Оценка изменчивости солнечной радиации производит­ся отношением ее максимальной величины к минималь­ной, выраженной в процентах. Наименьшая изменчи­вость суточных сумм суммарной и рассеянной радиации наблюдается в пустынных районах Земли, что объясня­ется малооблачностью погоды и преобладанием облаков верхнего яруса, мало ослабляющих солнечную радиа­цию. Наибольшее различие между максимальным и ми­нимальным значениями имеет место в прибрежных рай­онах умеренных широт, что объясняется большой измен­чивостью погодных условий. Наличие паров воды и пыли в воздухе значительно уменьшает интенсивность солнечной радиации.

Циркуляционные условия характеризуют перемещение воздушных масс (течений), несущих раз­личные количества тепла и влаги, а также изменение их свойств, сопровождающееся образованием поверхностей раздела между разными воздушными массами.

Циркуляционные процессы существенно влияют на формирование климата. Основными причинами общей циркуляции атмосферы является неодинаковое нагрева­ние Солнцем поверхности земного шара, а также вра­щение Земли, которое приводит к отклонению воздуш­ных течений (в северном полушарии в северо-восточном направлении).

Одним из важнейших факторов, определяющих такие элементы климата, как осадки, испарение, облачность, туманы, влажность, а также его континентальность яв­ляется влагооборот.



Рис. 1.2. Карта – диаграмма суточного хода суммарной радиации
Под влагооборотом понимают ряд последовательных физических процессов, происхо­дящих с водой: испарение, конденсация (образование облаков), выпадение осадков, а также перенос влаги. Влагооборот зависит от неравномерности нагревания суши и океана, наличия циркуляции воздушных масс и изменения свойств подстилающей поверх­ности. Влагооборот между сушей и океаном называ­ют внешним, а процесс испарения и конденсации в пределах ограниченной территории - внутренним. Внутренний влагооборот (рис. 1.3) определяет внешняя влага (r), которая частично выпадает (r1) на территорию в виде осадка, а частично выносится за ее пределы атмосферным стоком (с). Часть выпавших осад­ков испаряется (Е), а часть образует поверхностный сток (F).


Рис. 1.3. Внутренний влагооборот на ограниченной территории
При массовых гидрометеорологических наблюдениях измерениями учитывается количество выпавших осадков (r1) и величина испарившейся влаги (Е). Остальные со­ставные части влагооборота не определяются.

Одним из основных компонентов влагооборота явля­ется испарение, которое зависит от радиационного ба­ланса (энергетических ресурсов) и условий увлажнений поверхности Земли. Увеличение широты места и умень­шения солнечной радиации (энергетического ресурса) обусловливает убывание испарения. В тропических ши­ротах с большими энергетическими ресурсами фактором, определяющим испарение, являются условия увлажне­ния. Для характеристики возможного испарения с по­верхности достаточно увлажненной суши пользуются по­нятием испаряемости. Представляет интерес оценка отношения годовых сумм фактического испарения Е к ис­паряемости Е0 для средних многолетних условий. Ука­занное отношение можно использовать в качестве пока­зателя распределения влажности разных территорий (рис. 1.4).



Рис. 1.4 Распределение отношения годовых сумм испарения к испаряемости
Последним климатообразующим фактором являются местные физико-географические условия определенной территории. Физико-географические усло­вия характеризуются географической широтой, высотой над уровнем моря, различием форм рельефа (горные хребты, плоскогорья, возвышенности, низменности и т. п.), а также особенностями подстилающей поверх­ности. Под действием рассмотренных климатообразующих факторов формируются различные типы климатов отдельных зон Земли.

Известный климатолог Б. П. Алисов предложил по­строить классификацию климатов на основе изучения процессов радиации и атмосферной циркуляции в раз­личных широтах. Кроме того, выделяют горный климат, харак­теризующийся повышением разряженности воздуха и понижением температуры по мере увеличения высоты.

Важнейшими показателями термического режима яв­ляются абсолютные годовые минимумы и максимумы температуры. Основными факторами, определяющими изменение температуры, являются широта места, сте­пень континентальности и топографические условия.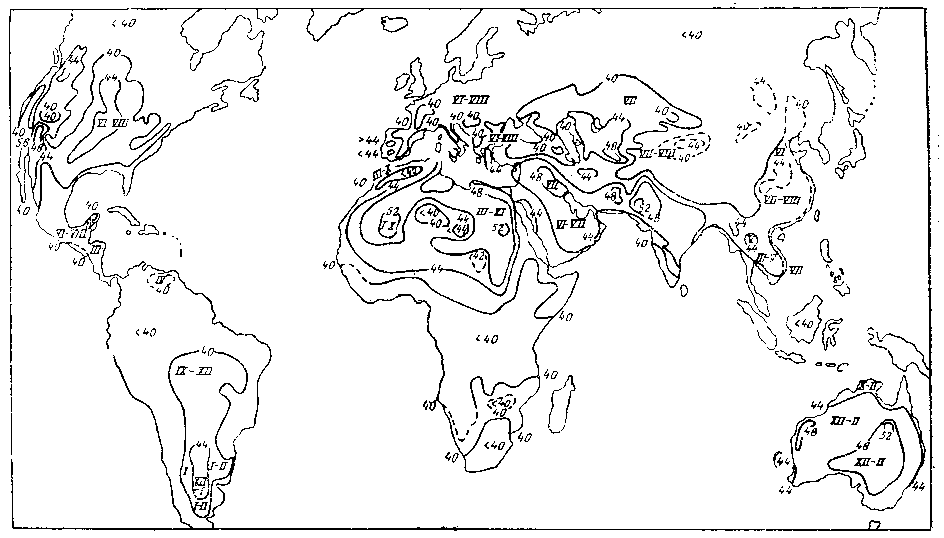



Рис. 1.5 Карта абсолютного максимума температуры воздуха
Влияние первых двух факторов приводит к плавному и последовательному изменению температуры. Распределение абсолютных годовых максимумов и минимумов в основном носит широтный характер, отражая влияние притока тепла от Солнца и особенности атмосферной циркуляции. Большое влияние оказывает также степень континентальности, влияние морей и океанов и характер подстилающей поверхности (ландшафт). Действие топографических условий (высота над уровнем моря и форма рельефа) нарушает плавный ход, и изменение температуры получает сложный характер.

Карта абсолютного максимума температуры воздуха показывает, что температура более 40° С на­блюдается до 50° умеренных широт.

Н 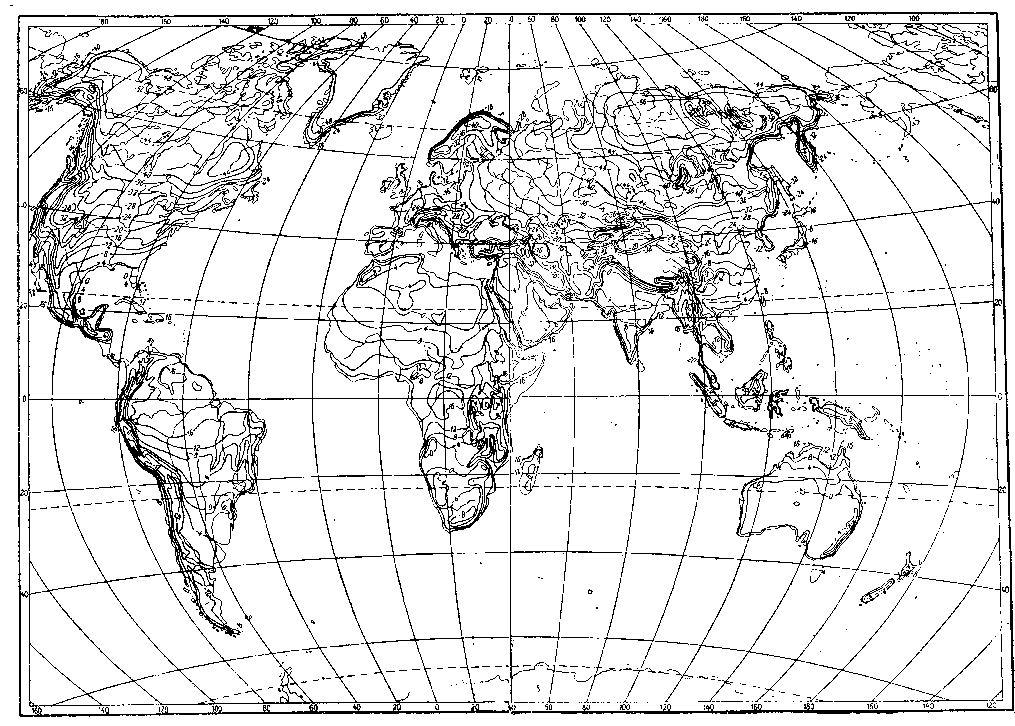а рис. 1.6 представлена карта средних из абсо­лютных годовых минимумов температур воздуха на зем­ном шаре.


Рис. 1.6. Представлена карта средних из абсо­лютных годовых минимумов температур воздуха на зем­ном шаре
Рассмотрение климатических условий приводит к вы­воду, что для различных типов климатов характерны различные сочетания и длительности воздействующих факторов.

При эксплуатации РЭА в некоторых специфических условиях иногда, кроме учета воздействия климатиче­ских факторов, следует также рассматривать воздейст­вие биологических факторов (плесени, различных ми­кроорганизмов, насекомых и грызунов).

Освоение космического пространства приводит к не­обходимости изучения воздействия космических условий на РЭА.

Помимо климатических воздействий, большинство видов РЭА в процессе своей эксплуатации и при транс­портировке подвергаются различным механическим воз­действиям. Результатом такого воздействия является возникновение вредного колебательного процесса, получившего название вибрация. Вибрацией принято также называть колебательное движение, воспроизводимое с испытательной целью специальными установками -вибрационными стендами и вибраторами.

Различают периодическую, гармоническую, импульс­ную и случайную вибрации. Частным случаем импульс­ной вибрации является одиночный механический им­пульс, называемый ударом. При этом полагают, что длительность импульса (tи) много меньше времени до его повторения (Т), а результирующий эффект (возникаю­щие силы, ускорения, скорости, смещения) - значите­лен.

Механические колебательные процессы характеризу­ются рядом параметров. Если условно колебательное движение изделия заменить колебательным движением точки, то мгновенное значение каждой из ее координат называют перемещением или вибрационным смещением и обозначают S(t).

Первая производная перемещения или вибрационно­го смещения называется соответственно колебательной или вибрационной скоростью: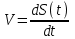

, (2)

а вторая производная - колебательным или вибрацион­ным ускорением: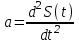

, (3)

В зависимости от направления перемещения рассма­триваемой точки тела вибрация может быть прямоли­нейной, плоскостной и объемной. При прямолинейной вибрации точка тела остается на одной прямой. По­скольку эта прямая может быть расположена под лю­бым углом у0 к горизонту, то возможны два крайних случая прямолинейной вибрации: горизонтальная и вертикальная.

При плоскостной вибрации рассматриваемая точка - тела перемещается в одной плоскости. Плоскостная ви­брация также может быть горизонтальной и вертикаль­ной. Кроме того, в зависимости от вида фигуры, описы­ваемой точкой тела, она может быть круговой, эллипти­ческой и т. д. Если рассматриваемая точка тела пере­мещается в некотором объеме пространства, то имеет место объемная вибрация.

Периодической вибрацией называется колебательный процесс, при котором все характеризующие его парамет­ры повторяются через одинаковые промежутки времени Т в неизменной последовательности.

Во многих практических случаях несколько колеба­тельных процессов могут протекать одновременно. При этом суммарный эффект определяется алгебраической суммой мгновенных значений колебательных величин, что приводит к маскировке основного процесса. Если мгновенные значения колебательной величины пропор­циональны синусу или косинусу линейной функции вре­мени

q = qa­­ sin (ωt+φ), (4)

q = qa cos (ωt+φ), (5)

то такой периодический колебательный процесс называ­ется гармоническим или синусоидальным.

Наибольшее абсолютное значение, достигаемое гар­монической колебательной величиной, называется ампли­тудой и обозначается qa, а аргумент (ωt+φ) в выраже­ниях для q называется фазовым углом.

Два колебания с одинаковой частотой называются синхронными. Наличие у таких колебаний различных начальных фазовых углов φ1 и φ­2 приводит к тому, что они оказываются сдвинутыми по фазе на угол ε = φ1-φ2.

Воспользовавшись выражениями (8) и (9), можно написать выражение для механического смеще­ния S:

S = Sa sin (ωt+φ); (6)

S = Sa cos (ωt+φ),

где Sa - амплитуда смещения; для скорости

V = ω Sa cos (ωt+φ) = Va cos (ωt+φ); (7)

V = -ω Sa sin (ωt+φ) = -Va sin (ωt+φ),

для ускорения

а = -ω2 Sa sin (ωt+φ) = -aa sin (ωt+φ) = -ω2 S; (8)

а = -ω2 Sa cos (ωt+φ) = -aa cos (ωt+φ) = -ω2 S.

Колебательное ускорение и смещение находятся в противофазе. Амплитуды смещения Sa, скорости Va и ускорения aa связаны соотношением

aa = ω V­a = ω2 Sa , (9)

или для числа колебаний в секунду

aa = (2πv)2Sa, (10)

где Sa - амплитуда смещения, мм;

v - частота колебаний, гц.

При большом числе измерений и вычислений удобно пользоваться номограммой, приведенной на рисунке 1.7, построенной на основании следующей формулы: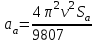

, (11)

где aa - амплитуда ускорения выражена в ga.

На практике удобно пользоваться упрощенной фор­мулой
aa ≈ 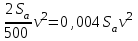, (12) где 2Sa - размах колебания.




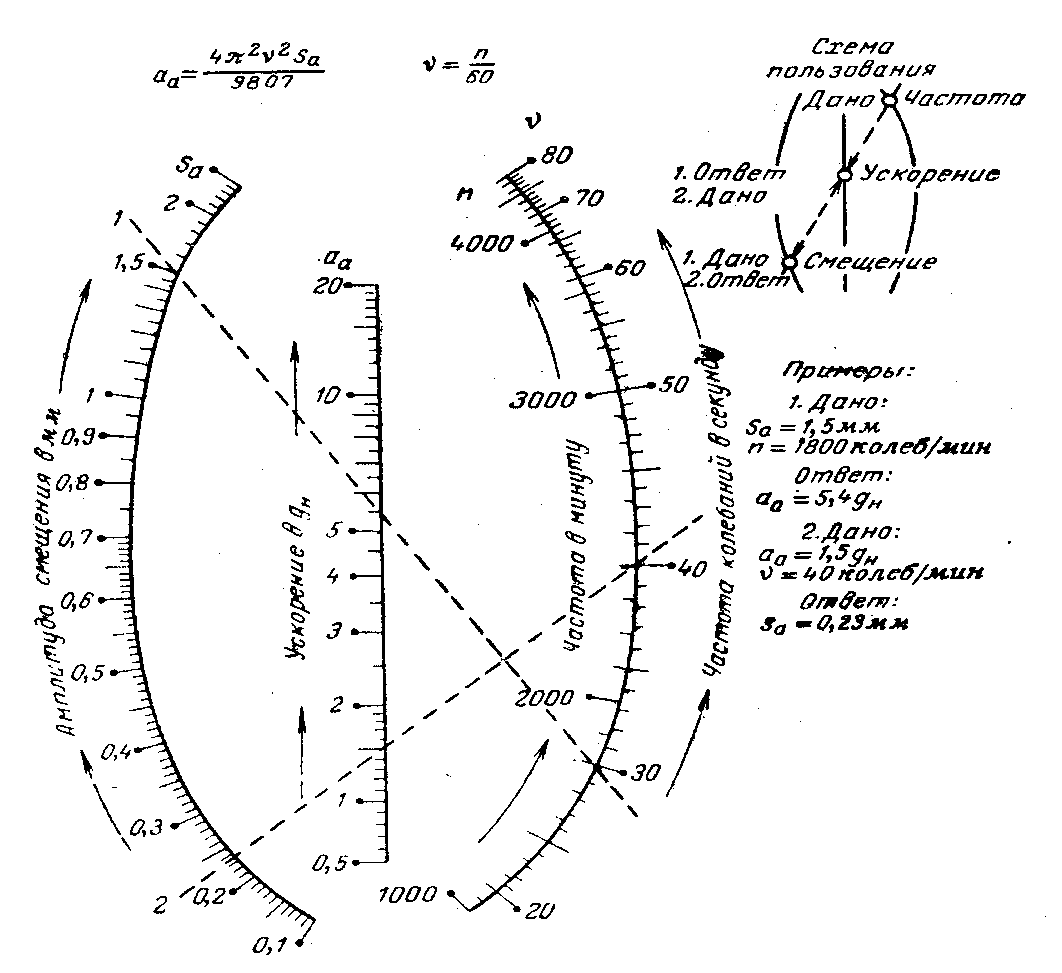Рис. 1.7. Номограмма для пересчета амплитуд смещения в амплитуду ускорения и обратно

Значения подсчитанные по формуле (6), получаются на 0,6% меньше, чем по формуле (5). Для сравнительной оценки интенсивности вибрации, выражаемой в величинах мощности Р, пользуются логарифмическими единицами -децибелами:

M=10lg 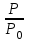, дб, (13)

где Р - интенсивность мощности вибрации относитель­но некоторой начальной мощности Р0.

Колебательный процесс, при котором в течение ко­нечных промежутков времени (пауз) колебательная ве­личина q = 0, а в течение промежутков времени tи от­лична от нуля, называется импульсным. Импульсные процессы бывают периодическими и непериодическими. Одиночные механические импульсы являются ударами.

На практике часто имеют место колебательные про­цессы (вибрация), при которых значения колебательной величины q1, q2, ... в различные моменты времени t1, t2,... являются случайными. Такие случайные вибраци­онные колебания можно представить себе как любые не­периодические и неповторяющиеся колебания. Случай­ную вибрацию можно описать как колебание, состоящее из последовательного ряда синусоидальных колебаний всех частот, в которых амплитуды и фазовые углы из­меняются случайным образом во времени.

Известно, что свойства колебательного процесса ха­рактеризуются его спектром. Различают амплитудный и фазовый спектры колебаний. Амплитудным спектром принято называть совокупность амплитуд гармонических составляющих колебания, а фазовым спектром - сово­купность их начальных фазовых углов.

Если гармонические составляющие колебания обла­дают дискретными значениями частот, то они образуют линейчатый спектр. Такой спектр имеют периодические колебания, у которых частоты членов тригонометриче­ского ряда Фурье изменяются от предыдущего члена к последующему ступенями, равными основной частоте колебания ω:

q(t)= 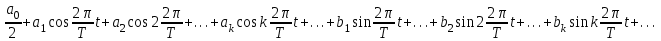, (14)

где a0, a1, a2, …, ak и b1, b2, …, bk коэффициенты Фурье.

Основную частоту периодических колебаний приня­то называть базисной. При гармонических колебаниях частоты более высокие, чем базисные, и кратные ей на­зывают высшими составляющими или составляющие высшего порядка (обертонами).

Величина i указывает кратность частоты данной гар­монической составляющей относительно основной часто­ты. Составляющая i-гo порядка равна произведению iv.

Для характеристики степени содержания в перио­дическом колебании обертонов (высших гармоник) поль­зуются коэффициентом гармоник (нелинейных искаже­ний), представляющим собой отношение корня квадратного из суммы квадратов амплитуд гармоник выше пер­вой к первой гармонике:

γ = 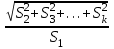. (15)

Если гармонические составляющие колебания обла­дают непрерывной последовательностью частот, то они образуют сплошной спектр, характерный для непериоди­ческих колебаний. Данный спектр содержит бесконечно большое число гармонических колебаний с бесконечно-малыми амплитудами.

Известно, что имеется связь между сплошным и ли­нейчатым спектрами с одной стороны и спектрами оди­ночного и повторяющегося импульсов с другой (рисунок 19). Если функция qи(t) описывает некоторый одиночный импульс длительности tи, а функция q(t) описывает периодический процесс, возникающий при по­вторении этого же импульса через промежутки време­ни Т, то можно показать, что линейчатый спектр перио­дической функции q(t) вписывается в сплошной спектр Sи (ω) функции qи(t) для одиночного импульса, причем чем меньше частота повторения импульсов Ω=2π/T, тем гуще расположены дискретные линии спектра (v = ω =i Ω). В пределе, когда имеет место одиночный импульс, эти линии заполняют всю ось ω и линейчатый спектр с амплитудами So, Si, Sa, ..., Si, переходит в сплошной.

Если имеют место беспорядочно следующие один за другим короткие импульсы, то соответствующий им энер­гетический спектр оказывается постоянным в диапазоне частот. Колебательный процесс, имеющий указанный выше спектр, называют белым шумом (белой вибраци­ей). На практике белый шум может иметь место при случайной вибрации, но он встречается крайне редко.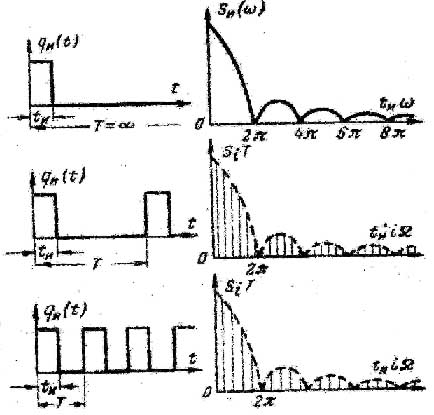



Рис. 1.8. Связь между амплитудными спектрами единичного и периодически повторяющегося импульсов.
Для наглядности спектр колебаний изображают гра­фически спектральной диаграммой. Чаще строят или по­лучают с помощью измерительной аппаратуры ампли­тудную спектральную диаграмму, у которой по оси абсцисс откладываются частоты v (или ω ) гармонических составляющих, входящих в состав колебательного про­цесса, а по оси ординат из точек соответствующих частот откладывают отрезки, пропорциональные значениям амплитуд.

Колебательное движение является одним из наибо­лее сложных процессов, так как колеблющаяся точка (тело, изделие) может иметь много степеней свободы и широкий частотный спектр колебаний. Для оценок различных колебательных процессов необходимо в общем случае получить сведения о шести независимых, коорди­натах (Sx, Sy, Sz, ax, ay, az,), определяющих положение изделия в пространстве, во времени за достаточно дли­тельный период. Такие сведения желательно иметь в виде осциллографических, магнитных и других видов за­писей, называемых виброграммами. Виброграммы чаще снимают для линейных смещений Sx(t), Sy(t), Sz(t), но они могут быть сняты и для угловых координат ax(t), ay(t), az(t). Пользуясь указанными данными, можно в принципе получить и другие параметры колебатель­ных процессов.