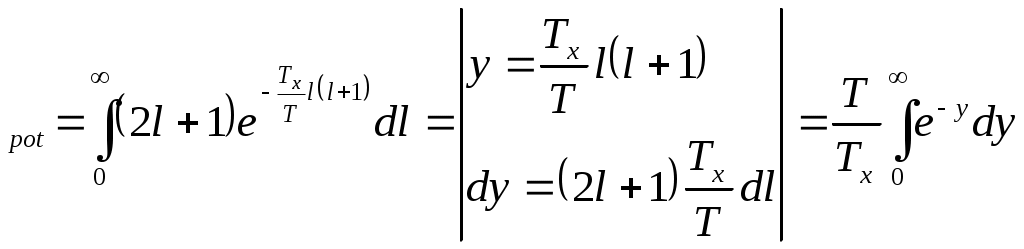|
|
лекциияяя. 4 Лекция. Лекция Статистикалы жйені тепе тедік жне тепе тедік емес кйлері
№4 Лекция
Статистикалық жүйенің тепе- теңдік және тепе- теңдік емес күйлері.
Макрожүйенің әрбір макробөлігінің физикалық шамалары флуктуация аймағында ортақ болса, ондай жүйені біз тепе-теңдік күйде орналасқан жүйе дейміз. Ал айтылған шарт орындалмаса , жүйе күйі - тепе-теңдік емес.
1.4. Микроканондық үлестіру функциясы
Берілген жүйе тұйықталған болсын. Жүйенің күйі тепе-теңдік делік. Жүйе тұйықталған болса, оны адиабаталық жүйе деп аталады. Себебі орта мен жүйе арасында алмасу процесстері жүрмейді. Жүйе адиабаталық жағдайда болғанымен , жүйе энергиясы өзгермейтін шама 
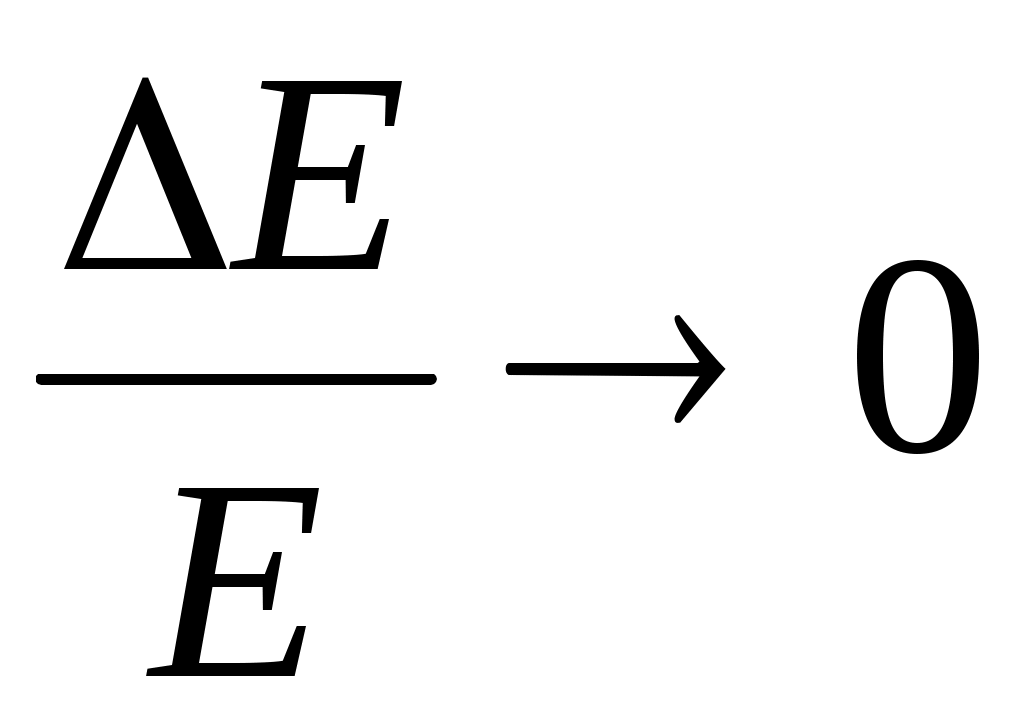 болады. E=E0= const. болады. E=E0= const.
Мұндай жүйені сипаттау үшін үлестіру функциясын δ функция түрінде алуға болады.

w(x)=δ( E-E0) (11) –Дерак δ функциясы .
δ функциясының нормалануы-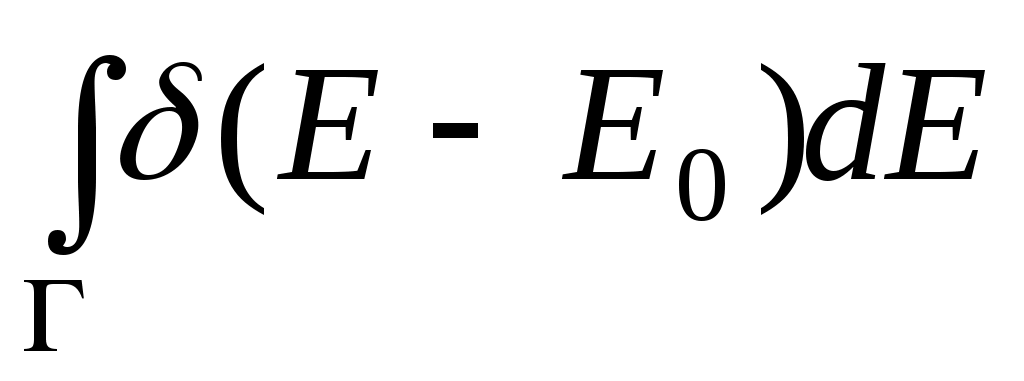 =1 (12) =1 (12)
Анықтама бойынша,
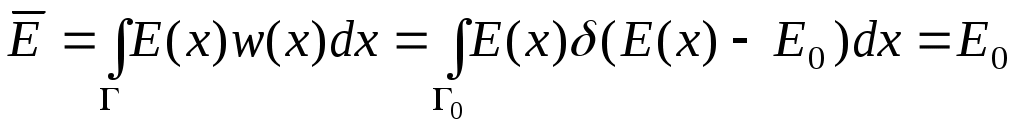 (13) (13)
Осыдан шығатыны, 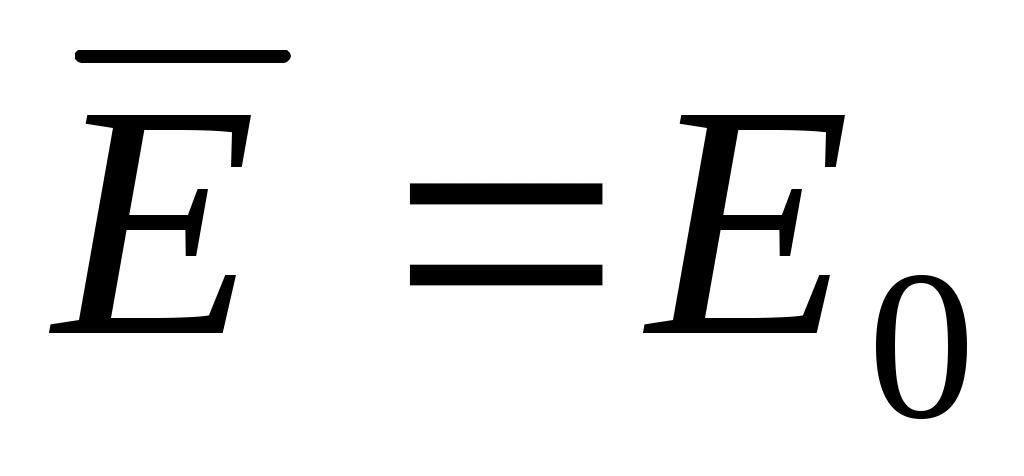 (14) (14)
Жүйені сипаттайтын басқа физикалық шамалады энергия арқылы анықтап, олардың орташа мәнін келесі теңдеу арқылы табуға болады.
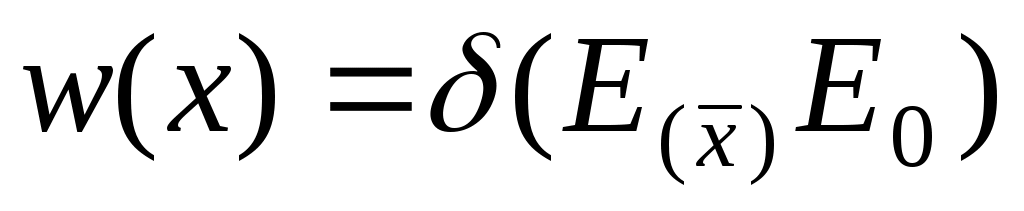
w(x)= δ (E(x)-E0) , (график керек) , (график керек)
Энтропия
Статистикалық физикада берілген анықтамада термодинамикадан алынған келесі шарттарға сәйкес болу керек.
1. Энтропияның дифференциалы - dS , dS = dQ / T
2. Энтропия адитивті шама ,яғни адитивті функция.
Жүйе бірнеше бөліктерден құралса , жүйенің толық энтропиясы бөліктерінің энтропияларының қосындысына тең болады.
S= S1+S2
3. Жүйе энтропиясы кемімейтін шама болып келеді.
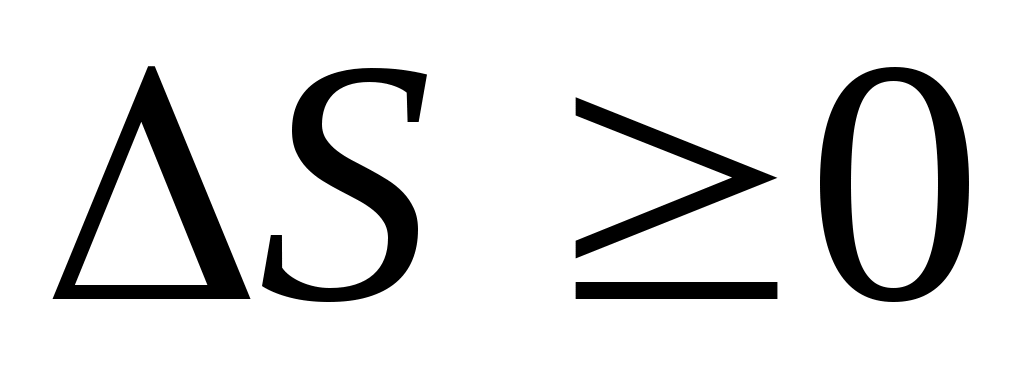
Аталған үш шартты ескере отырып, энтропияның анықтамасын берейік.
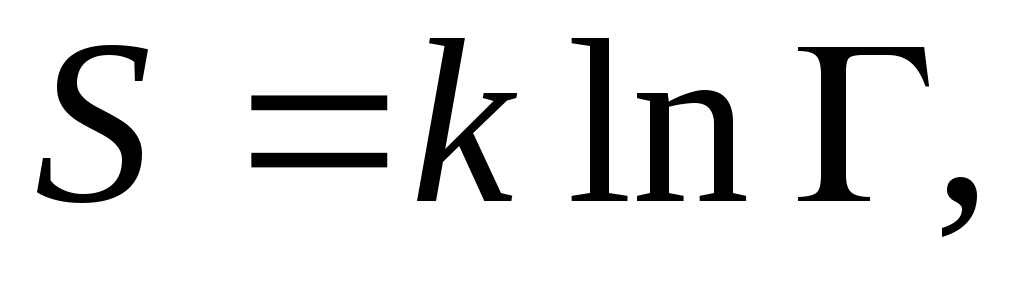 (16) (16)
k- const., Γ- жүйенің фазалық көлемі.
(16) берілген анықтама жоғарыдағы шарттармен сәйкес болатынын немесе сәйкес еместігін тексеріп көрейік.
Бізге берілген статистикалық жүйені екі бөлікке бөлейік.
N=N1+N2 ,
Бөлшек саны қосылса, фазалық көлем көбейеді .
Γ= Γ 1*Γ 2(17)
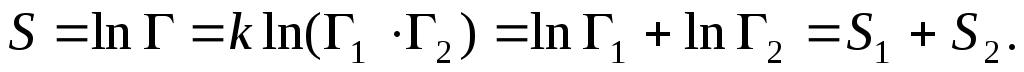
Яғни , S= S1+S2 , бұл екінші шарт. Ал үшінші шартты дәлелдеу үшін жүйенің тепе- теңдік күйінде орналасқан энтропияның максимал екенін дәлелдейік.
dw= w(x) d Γ (18)
dΓ - фазалық көлем
w- ықтималдық
Жүйенің d Γ фазалық көлемінің орналасу ықтималдығы dw
Ықтималдық фазалық көлемге пропорционал.
dw dΓ
Жүйе тепе- теңдік емес күйден тепе- теңдік күйге ауысса, жүйенің кем ықтималдығы максимал ықтималдыққа ауысады. Тепе- теңдік күйде статистикалық жүйе орналасуы максимал .
max dw =>max dΓ
max dΓ=>max S
(16) берілген анықтама энтропия шарттарының үшіншісіне сәйкес келеді.
S=k ln Γ
S2= k ln Γ2=k ln (V2N)
S1= k ln Γ1=k ln (V1N)
ΔS=S2 –S1 = k ln V2N- k ln V1N =k ln (V2 /V1)N =
k ln (2V1 / V1)N= k ln 2N= kN ln2;
ΔS=S2 –S1 = kN ln2
ΔS= kN ln2 , ΔS>0
№ 13,14 лекциялар
Екі атомдық идеал газ жүйесінің үлесті жылу сыйымдылығының кванттық теориясы.
Екі атомдық идеал газ жүйесін қарастырамыз. Идеал газдың әр молекуласы екі атомдан құралған. Молекулаға кіретін екі атомның салыстырмалы қозғалыстары екі түрлі болуы мүмкін:
а) тербелмелі қозғалыс;
б) айналмалы қозғалыс.
Кванттық көзқарас бойынша теория құрған себебінен молекулаға кірген атомдардың тербелмелі қозғалысын кванттық вибратор немесе кванттық осциллятор, айналмалы қозғалысын кванттық ротатор ретінде талдаймыз.
Кванттық осциллятор және кванттық ротатор.
Кванттық осциллятор берілген. Осциллятор жүйесін сипаттау үшін Шредингер теңдеуінің шешімін анықтауға тиістіміз.
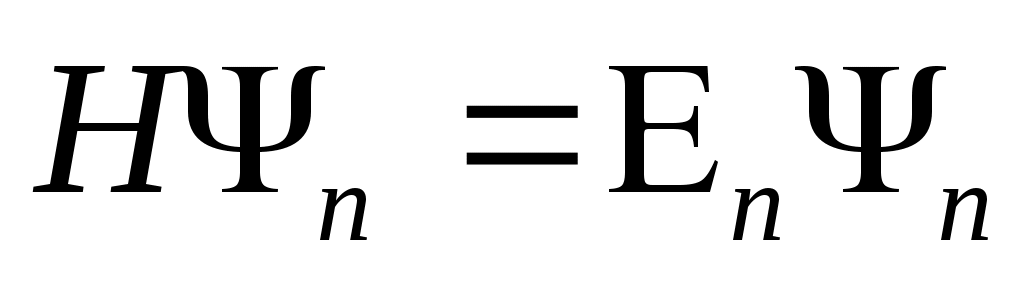 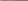 
n=0, E0=h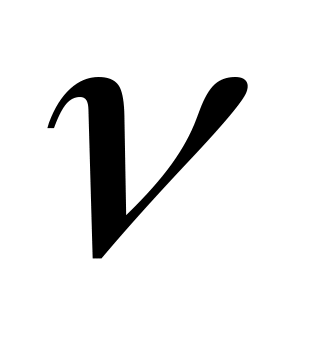 0/2 0/2
n=1, E1=3h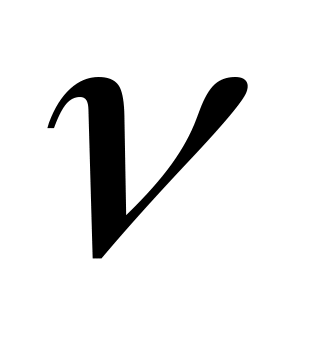 0/2 0/2
n=2, E2=5h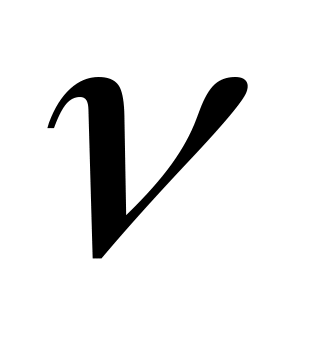 0/2 0/2
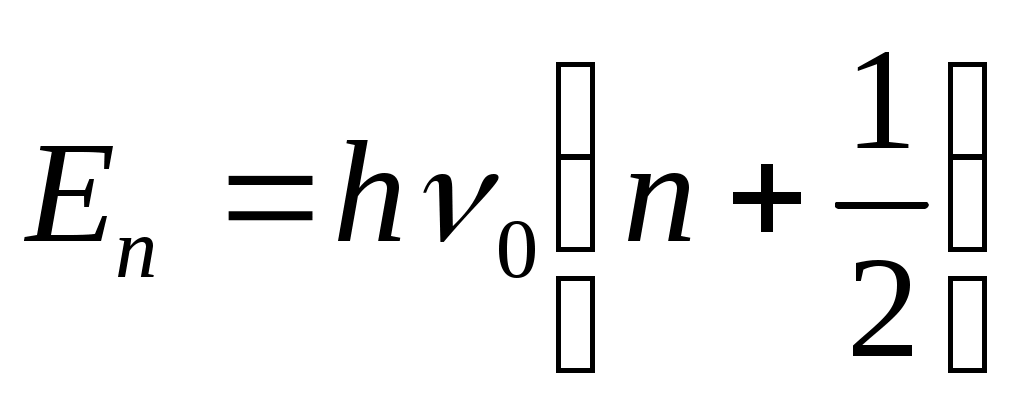 n = 0, 1, 2,... n = 0, 1, 2,...
Е п - гармоникалық осциллятордың энергиясы. п - гармоникалық осциллятордың энергиясы.
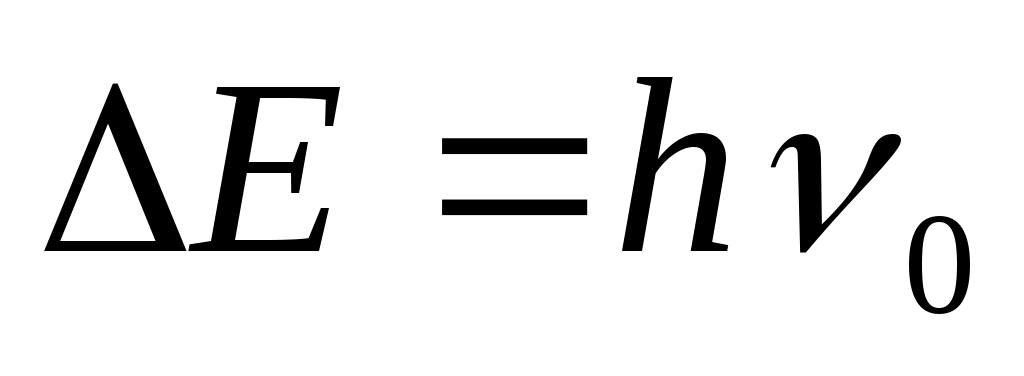  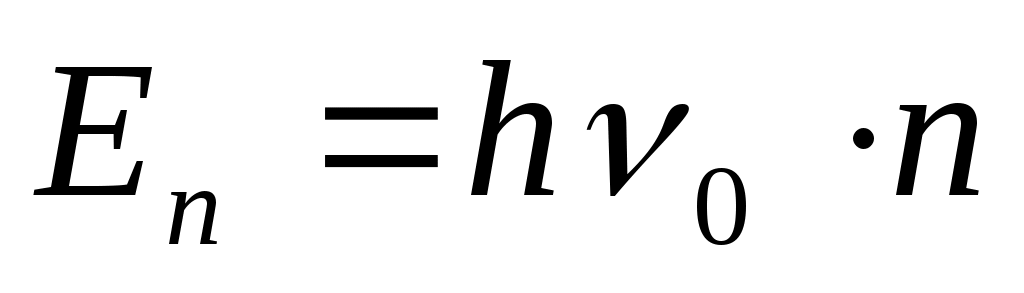 (1) (1)
 Ротатор дегеніміз – шеңбер бойымен қозғалатын Ротатор дегеніміз – шеңбер бойымен қозғалатын
материалдық нүкте.
Классикалық физикада шеңбер бойымен қозғалатын материалдық нүктенің энергиясы былай жазылады:
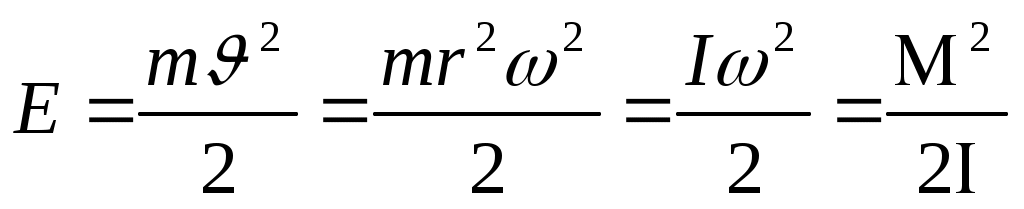 (2) (2)
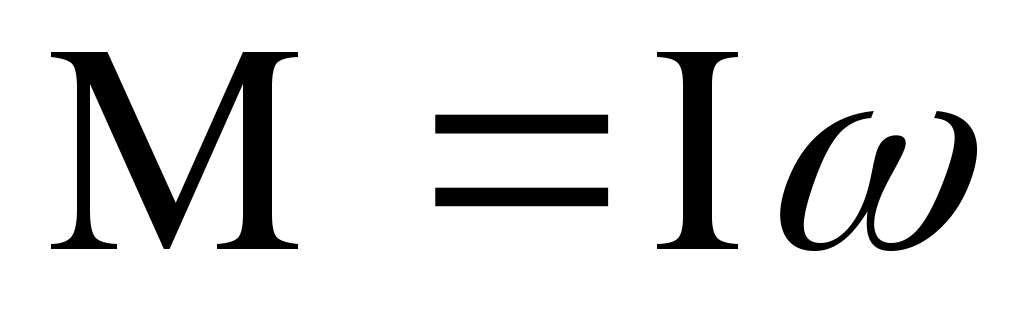 - бұрыштық момент, I = mr2 – инерция моменті. Сәйкестік принципін қолданып, (2)-ні кванттық физика бойынша анықтаймыз. Ол үшін бұрыштық момент орнына бұрыштық момент операторын қолданымыз: - бұрыштық момент, I = mr2 – инерция моменті. Сәйкестік принципін қолданып, (2)-ні кванттық физика бойынша анықтаймыз. Ол үшін бұрыштық момент орнына бұрыштық момент операторын қолданымыз:
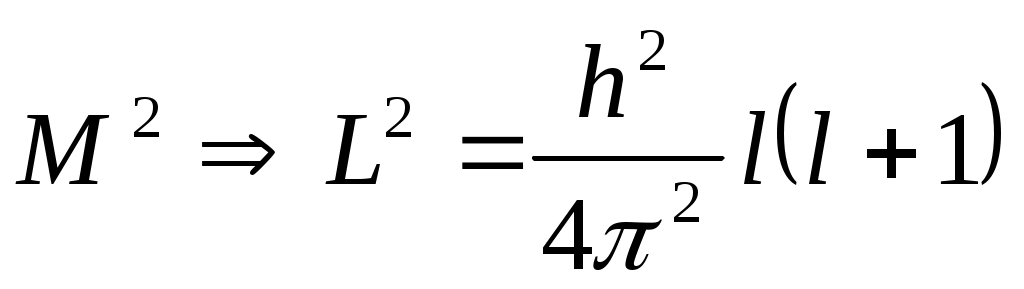 l= 0, 1, 2, 3, ...(3) l= 0, 1, 2, 3, ...(3)
l – орбиталды квант саны. Орбиталды квант санының проекциясы былай жазылады: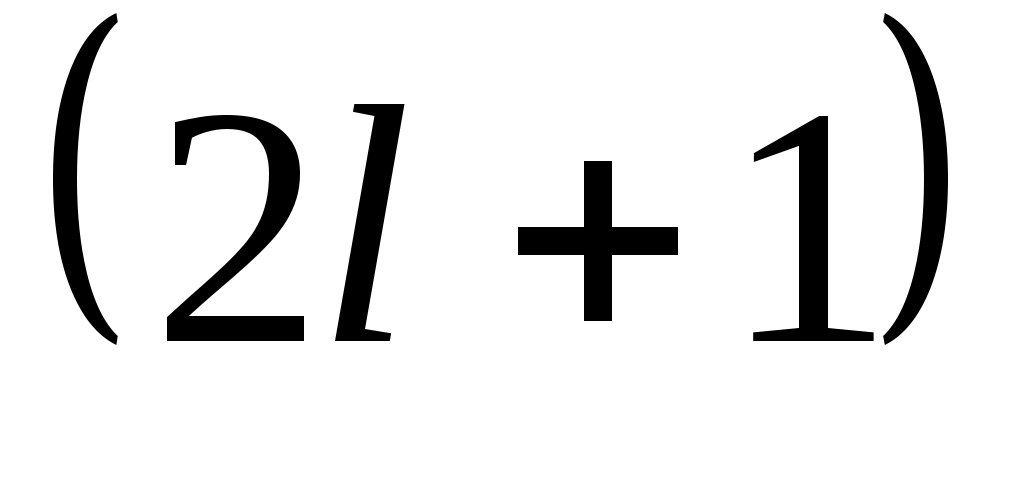 . Сол себептен әр күй . Сол себептен әр күй 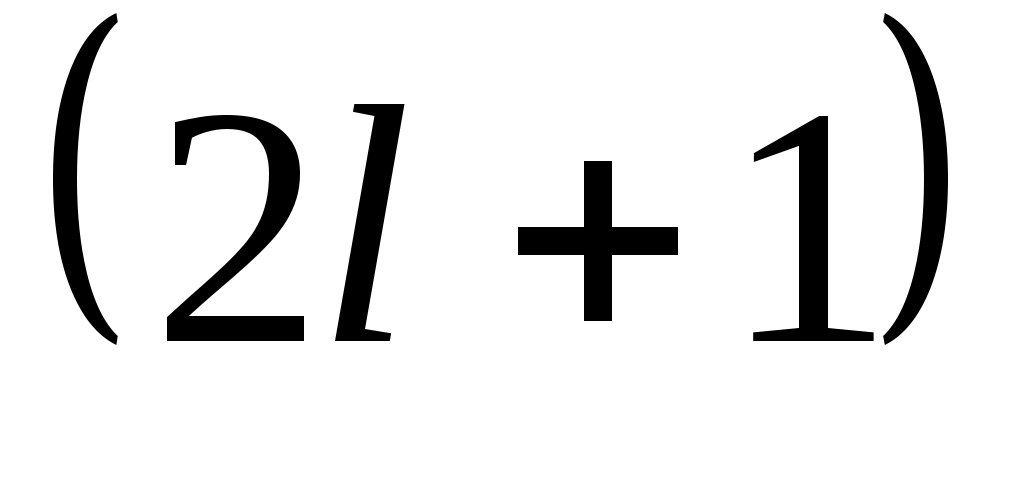 рет азғынады. рет азғынады. 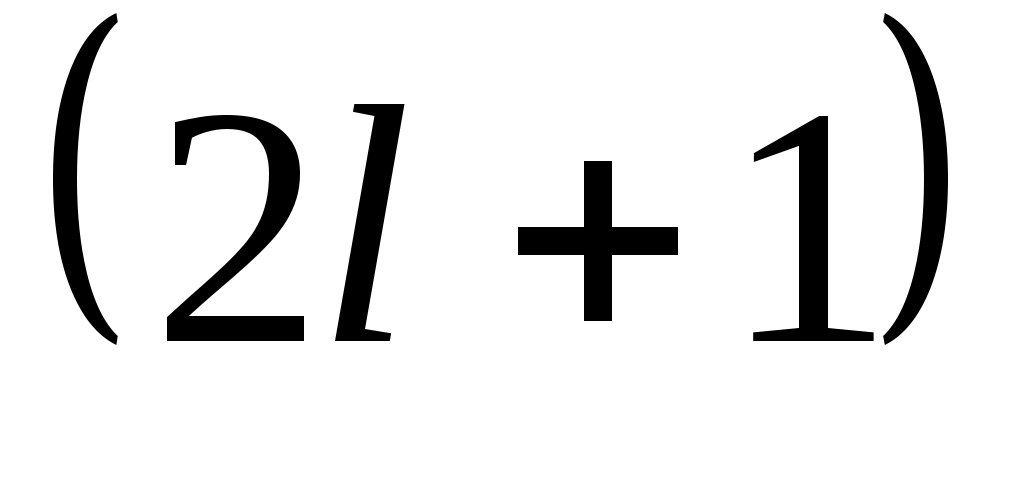 - кванттық күйін азғындау еселігі деп аталады. - кванттық күйін азғындау еселігі деп аталады.
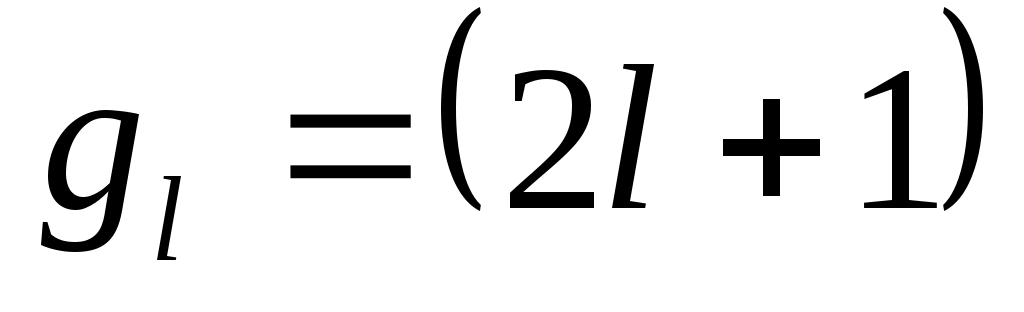
(3) – ті ротатордың энергиясын анықтауға қолданамыз:
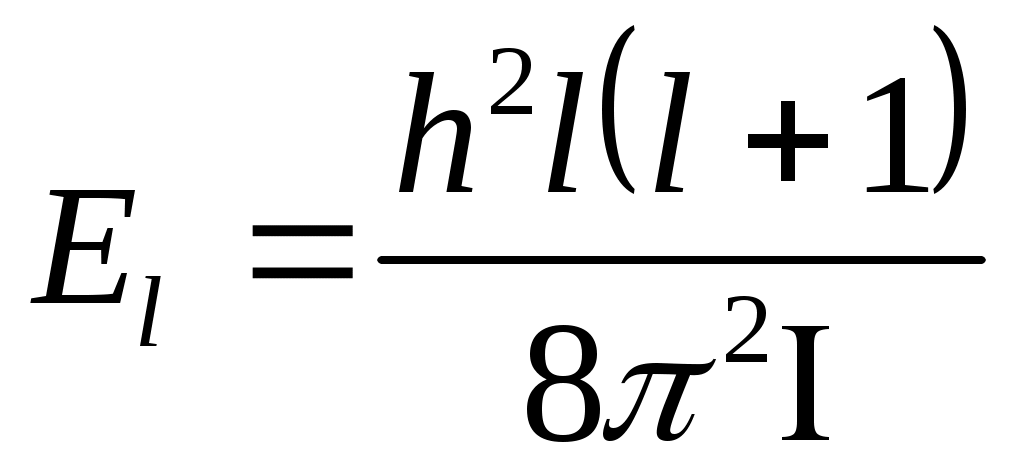 (4) (4)
Кванттық осциллятор жүйесінің статистикалық қосындысы.
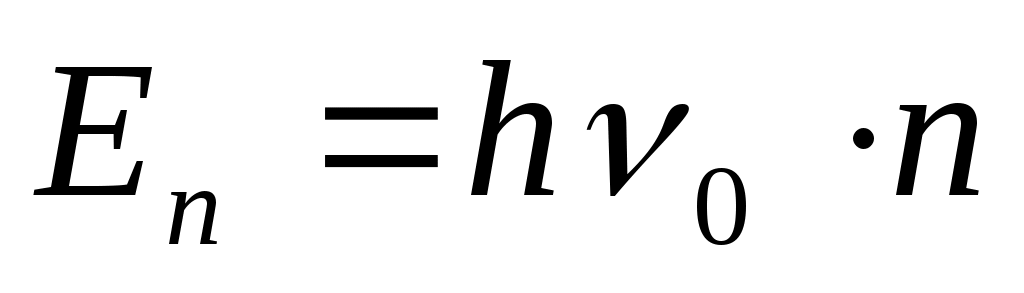
Кванттық осциллятор жүйесінің статистикалық қосындысын есептейміз. п - кванттық осциллятордан құралған жүйенің статистикалық қосындысын келесі теңдеу арқылы анықтауға болады.
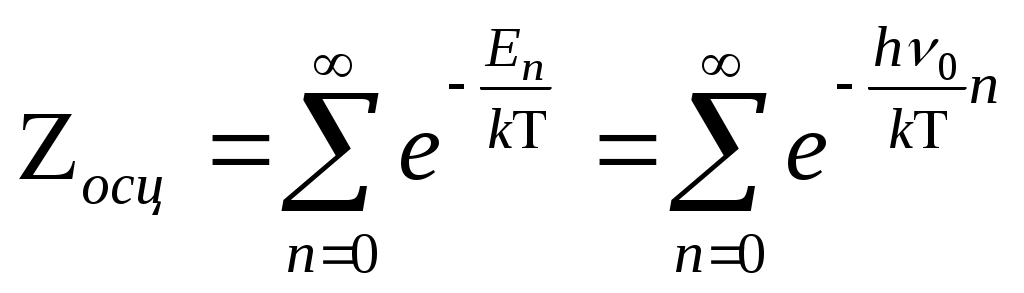 (1) (1)
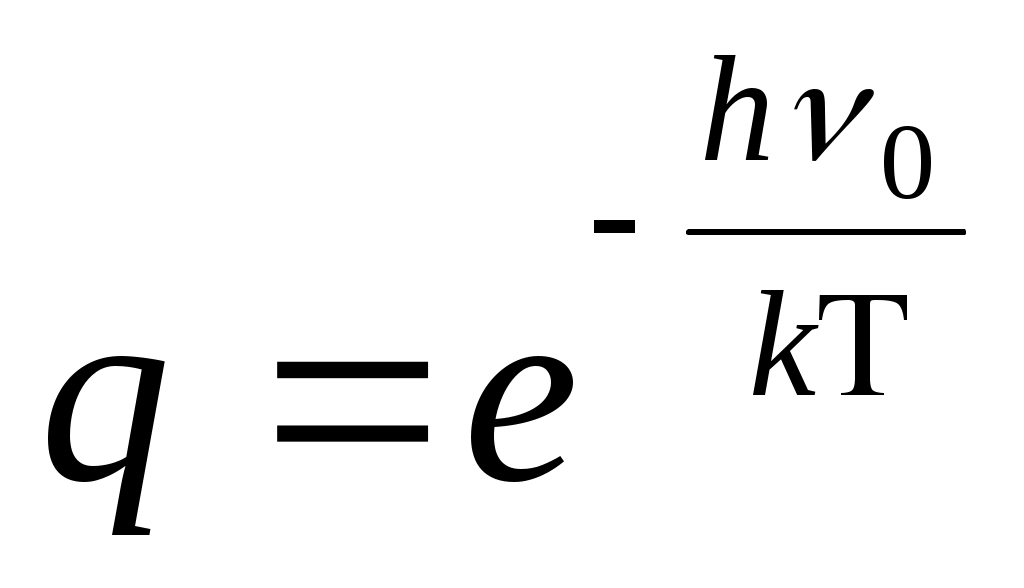 , а1 1 – геометриялық прогрессия. , а1 1 – геометриялық прогрессия.
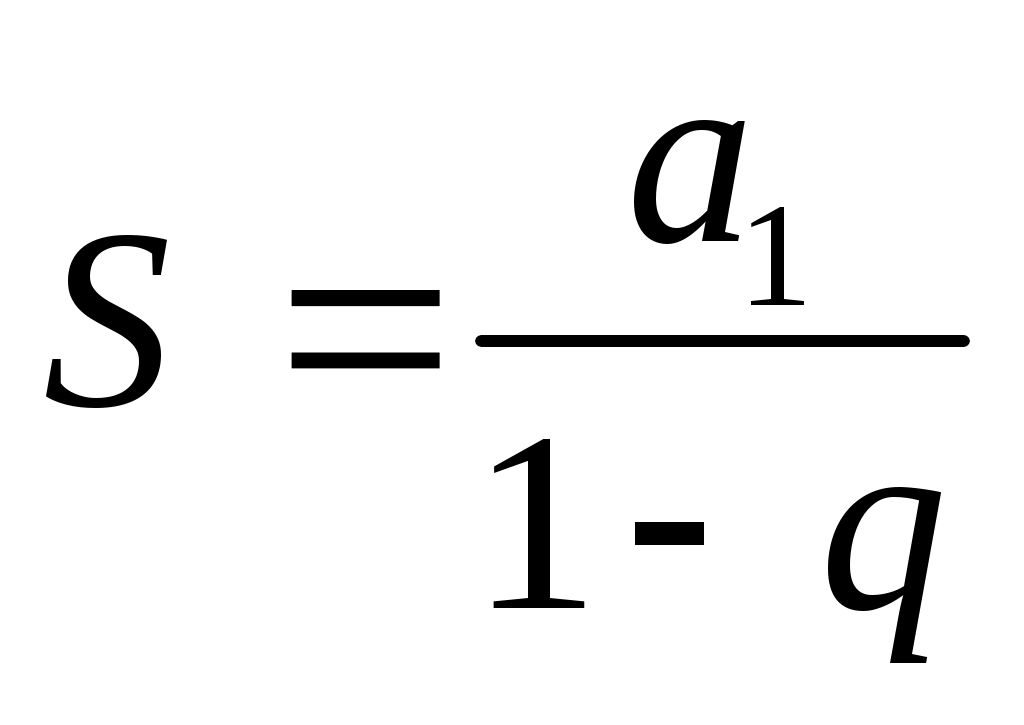 - геометриялық прогрессияның қосындысы. - геометриялық прогрессияның қосындысы.
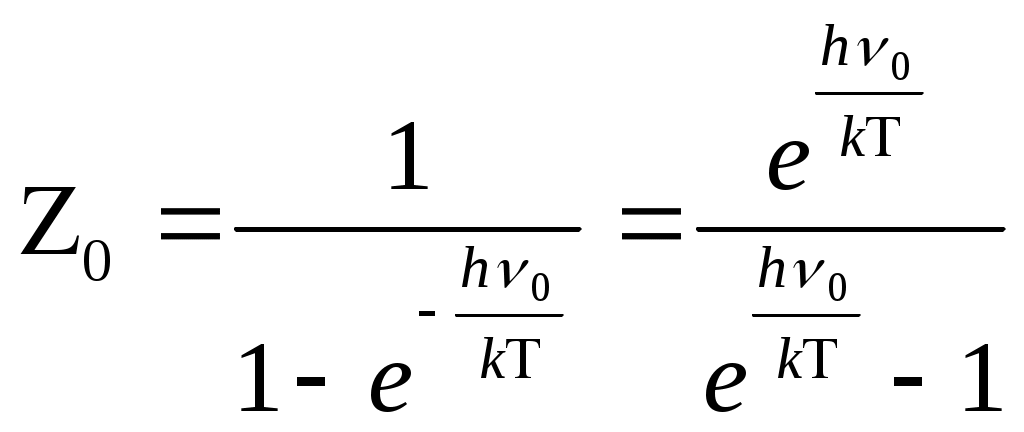 (2) (2)
(2) –ні қолданып, п - кванттық осциллятордан құралған жүйенің энергиясын табайық:
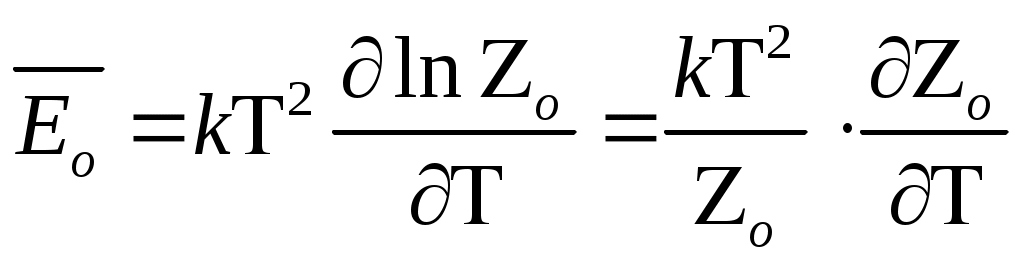
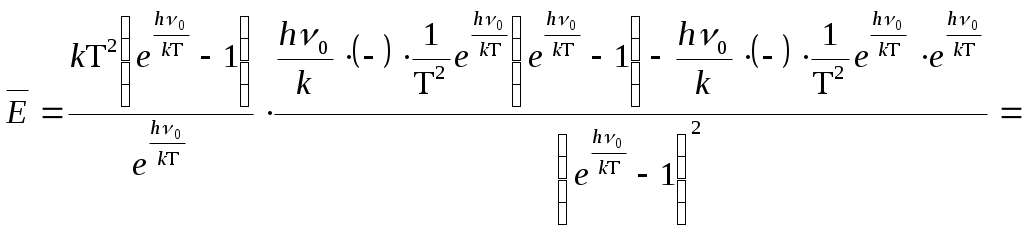
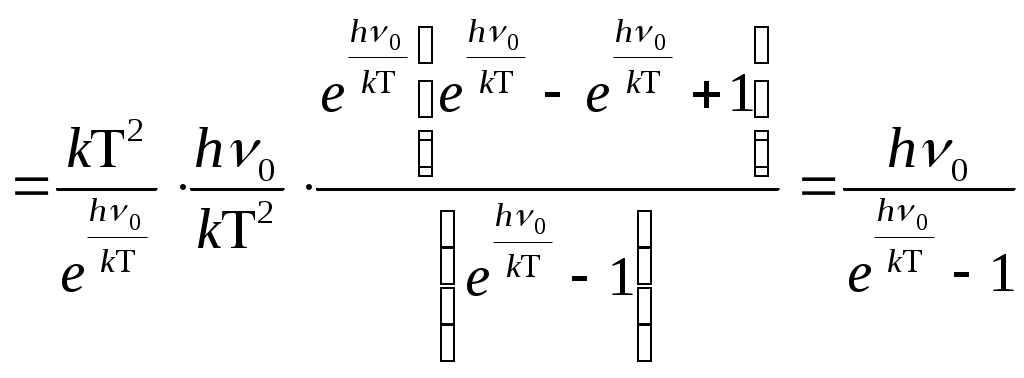
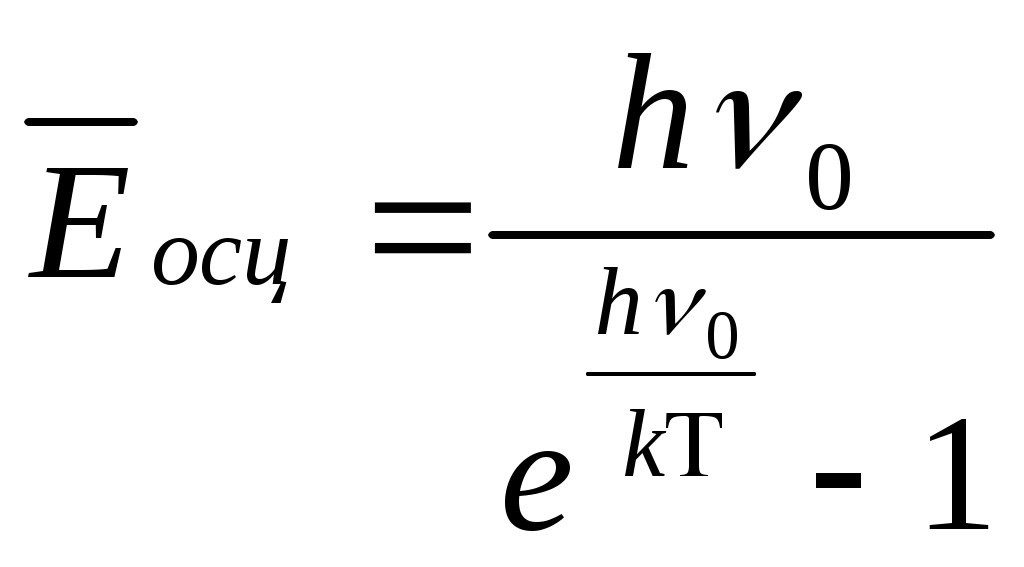 (3) (3)
(3) – бір осциллятордың энергиясының орташа мәні.
Т 0 болғанда, Е 0 болады.
Т , 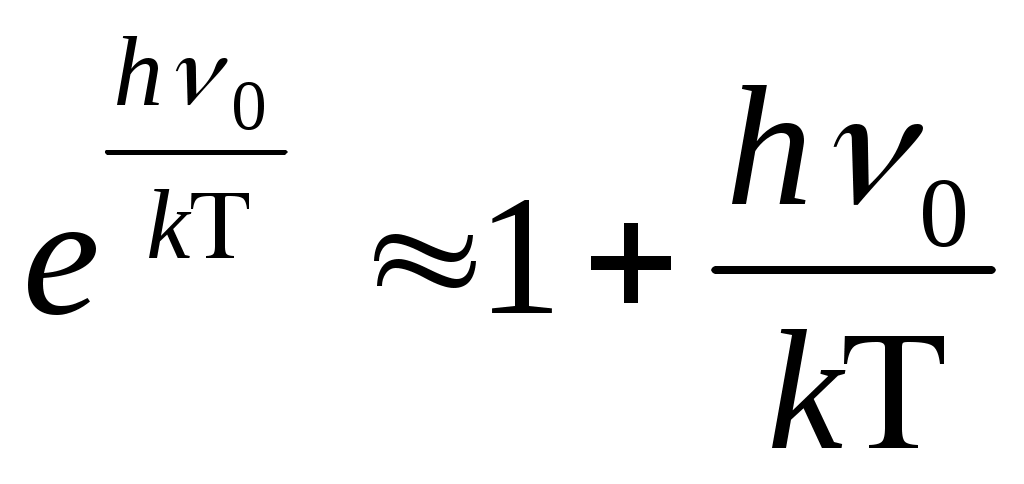 , , 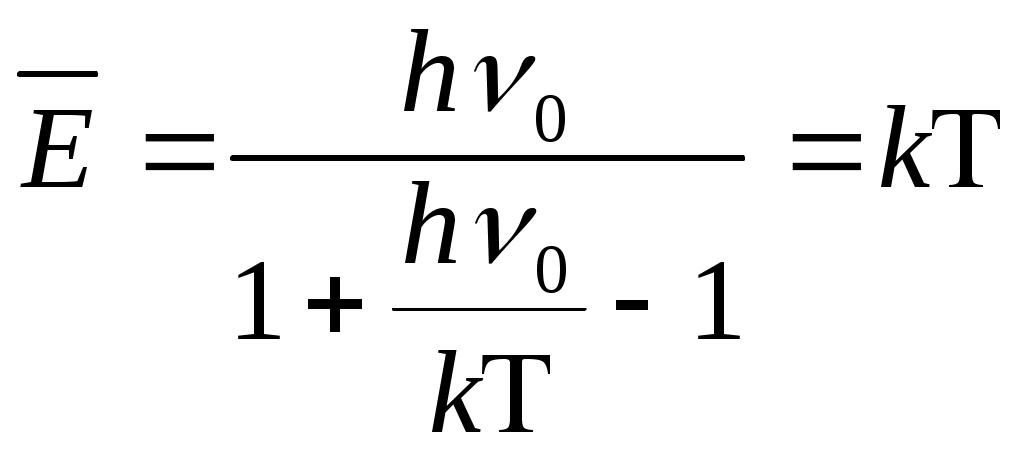
Т ,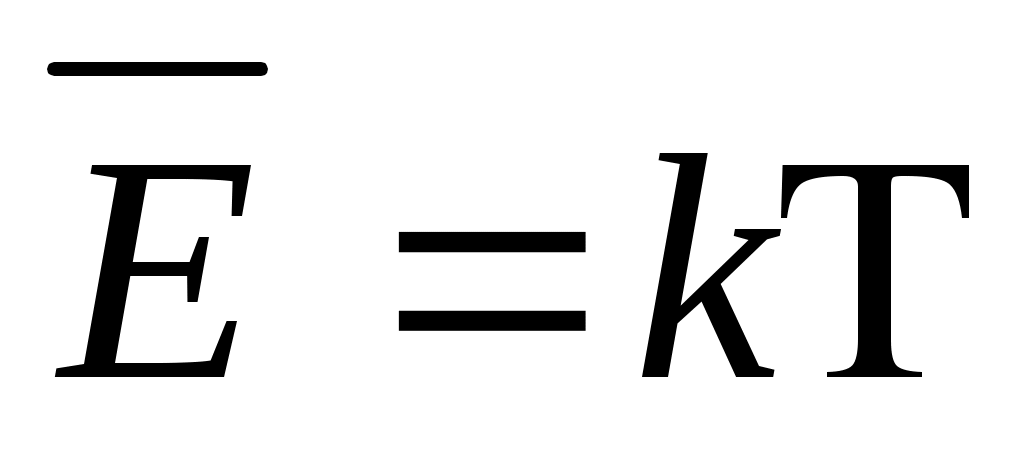 , N =N0 , R=kN0 , E = RT , N =N0 , R=kN0 , E = RT
Біросциллятордың үлесті жылу сыйымдылығы:
Т 0, CV = 0.
Т , CV = kN, N = N0 , CV = R.
Екі атомдық идеал газ жүйесінің үлесті жылу сыйымдылығының кванттық теориясы.
Кванттық ротатор жүйесінің үлесті жылу сыйымдылығы.
Материалдық нүкте шеңбер бойынша қоғалады.Олай болса, оның кинетикалық энергиясы Е=mv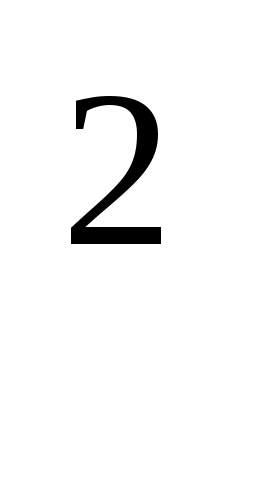 /2 болады немесе /2 болады немесе 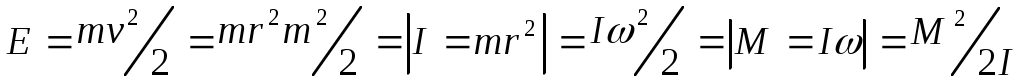
Сонда
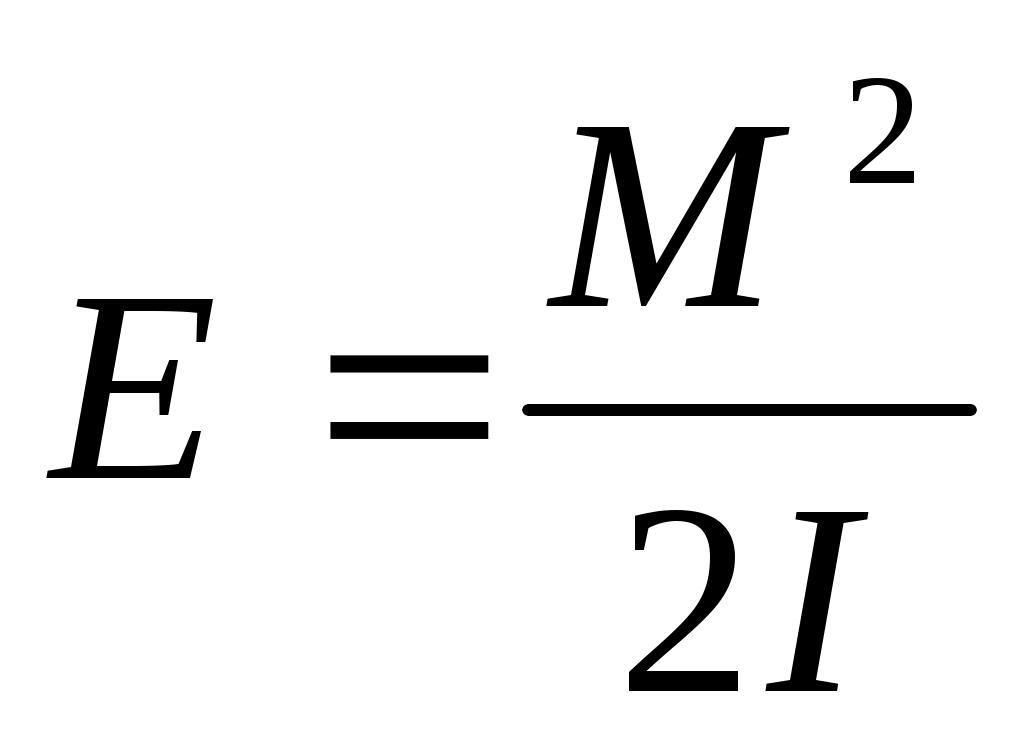 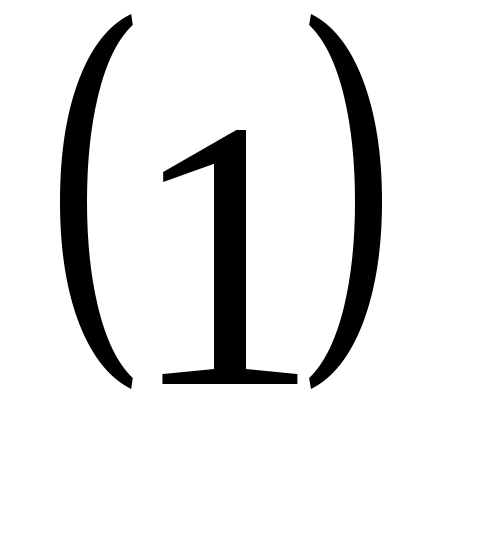
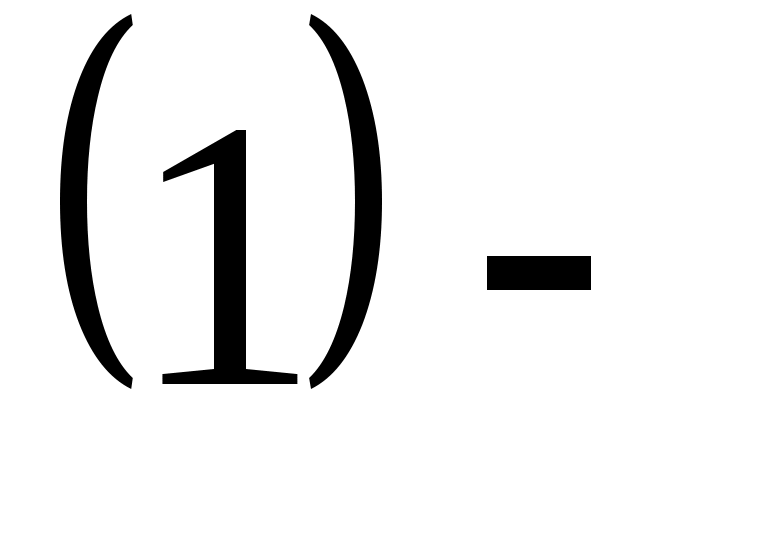 классикалық механикада энергияны анықтайтын формула. классикалық механикада энергияны анықтайтын формула.
М- бұрыштық момент, I- инерция моменті
Енді біз сәйкестік принципті қолданып,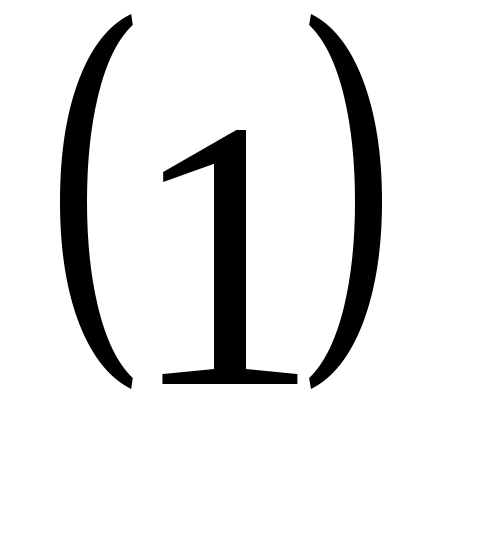 - інші формуланы кванттық физикасы бойынша анықтайық.Ол үшін бұрыштық момент орнына біз сіздермен бұрыштық момент операторын қолданамыз. - інші формуланы кванттық физикасы бойынша анықтайық.Ол үшін бұрыштық момент орнына біз сіздермен бұрыштық момент операторын қолданамыз.
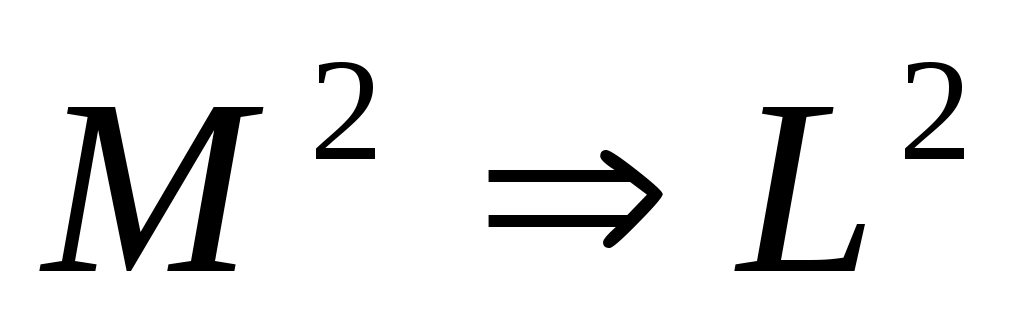
Осы 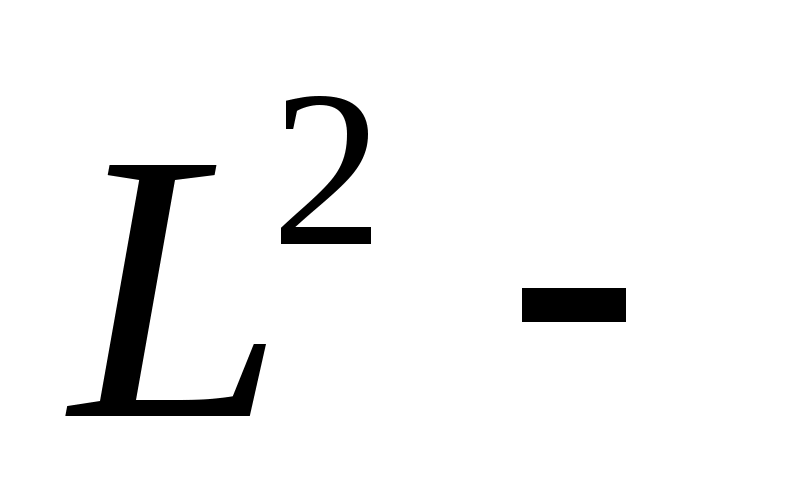 тың мәні келесі теңдеумен анықталады. тың мәні келесі теңдеумен анықталады.
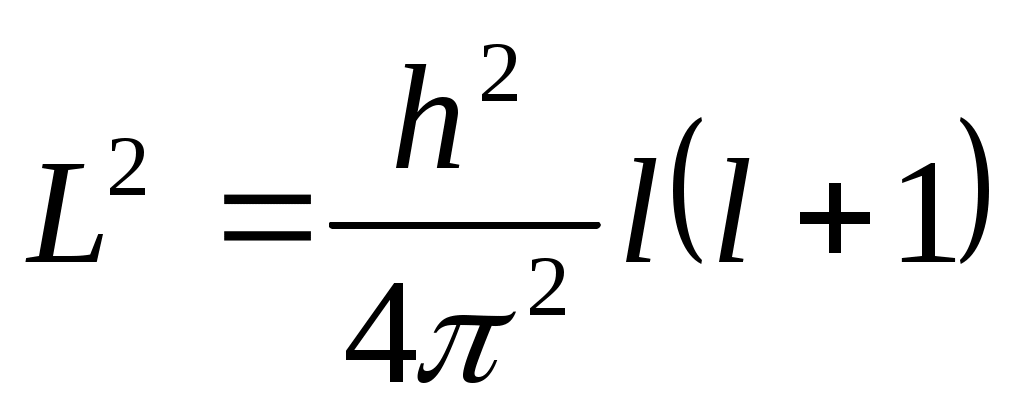 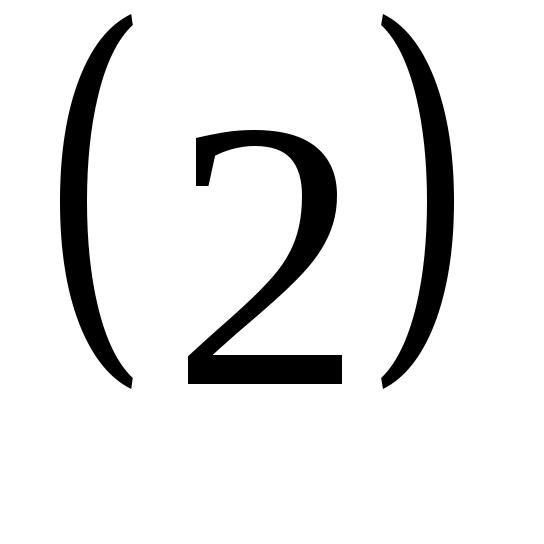
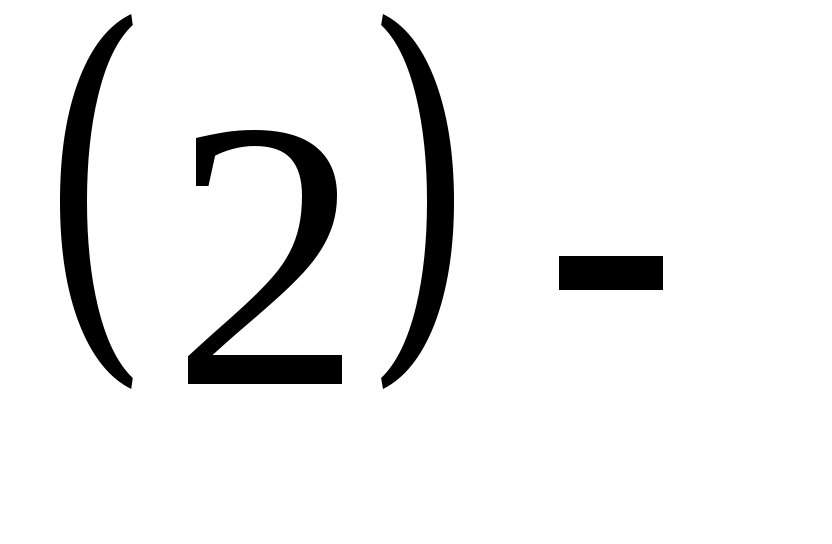 ші формуладағы шамалар: ші формуладағы шамалар:
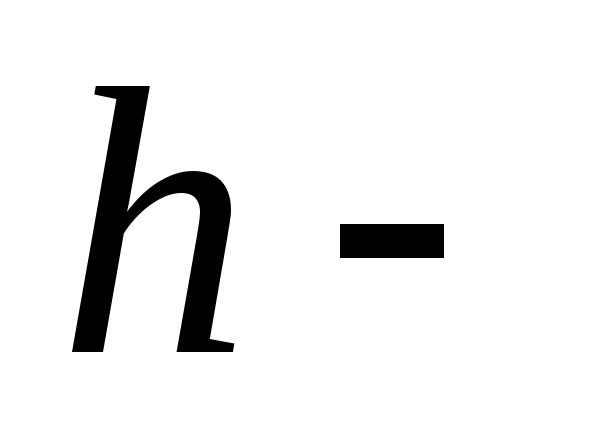 кванттық тұрақты, кванттық тұрақты,
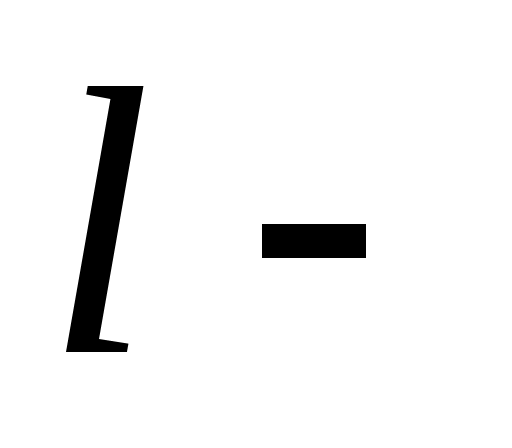 бұрыштық моменттің квант саны немесе орбитальдық кванттық сан. бұрыштық моменттің квант саны немесе орбитальдық кванттық сан.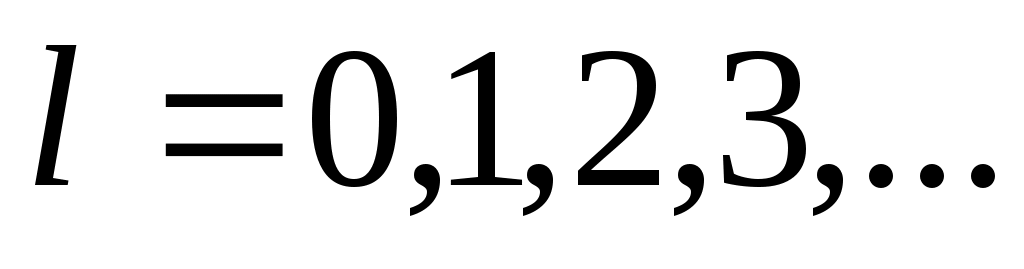 Орбитальдық кванттық сан Орбитальдық кванттық сан 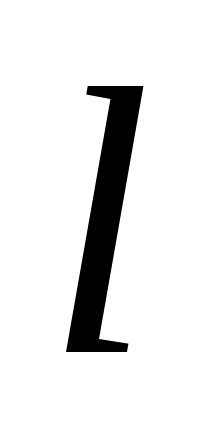 -дің -дің 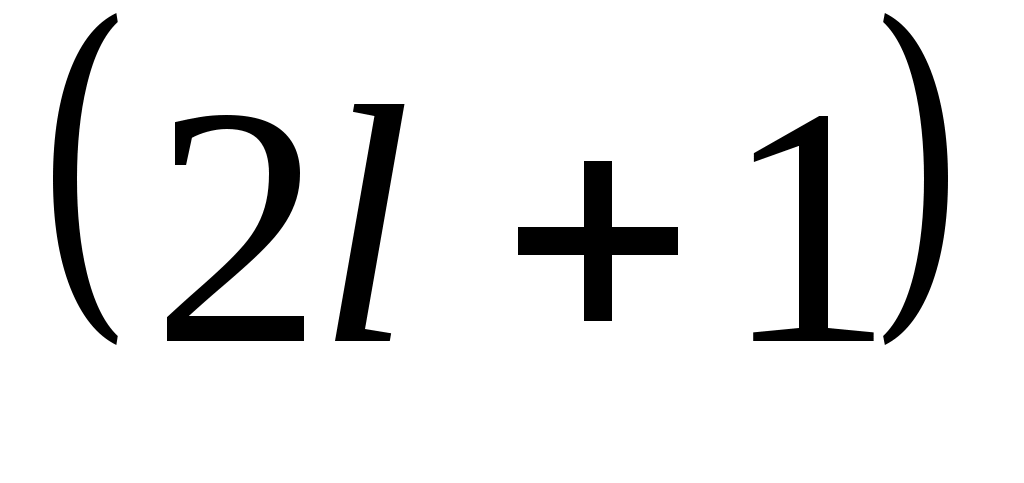 проекциясы болады. проекциясы болады.
Мысалы: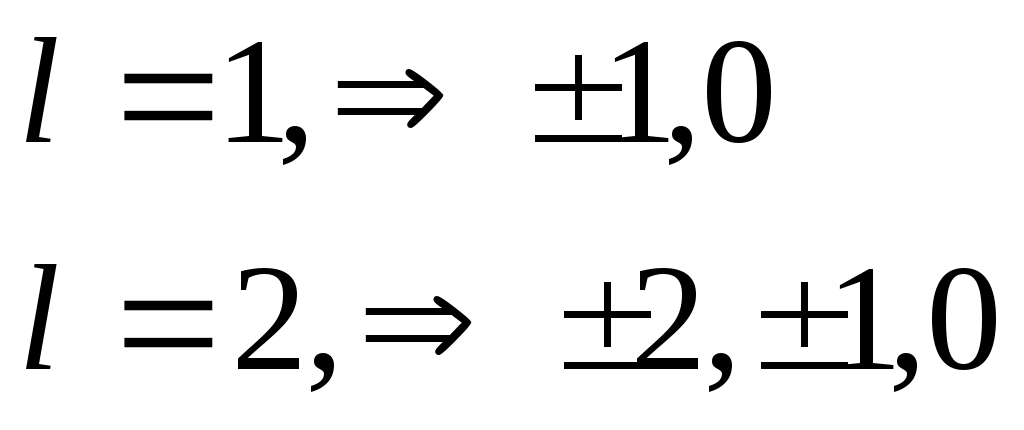
Сол себептен әр күй 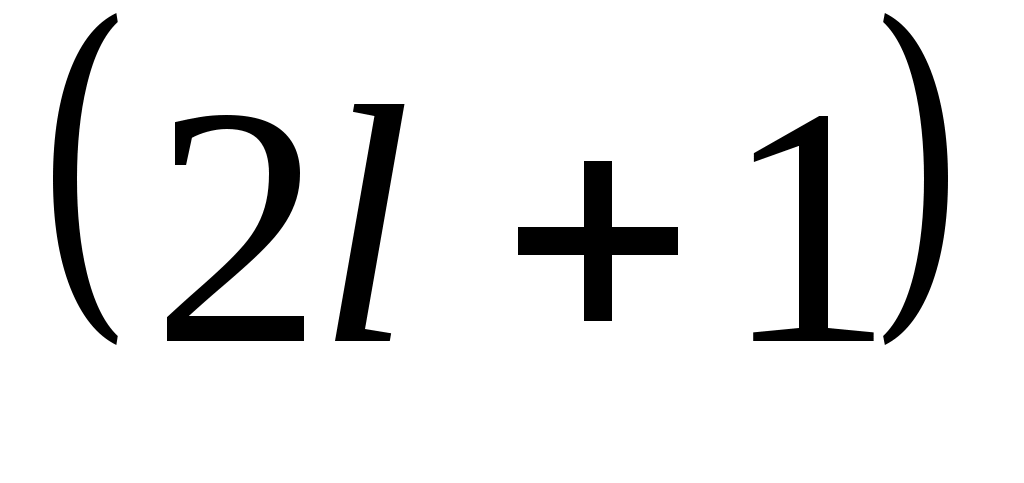 рет азғынады (генерацияланады). рет азғынады (генерацияланады).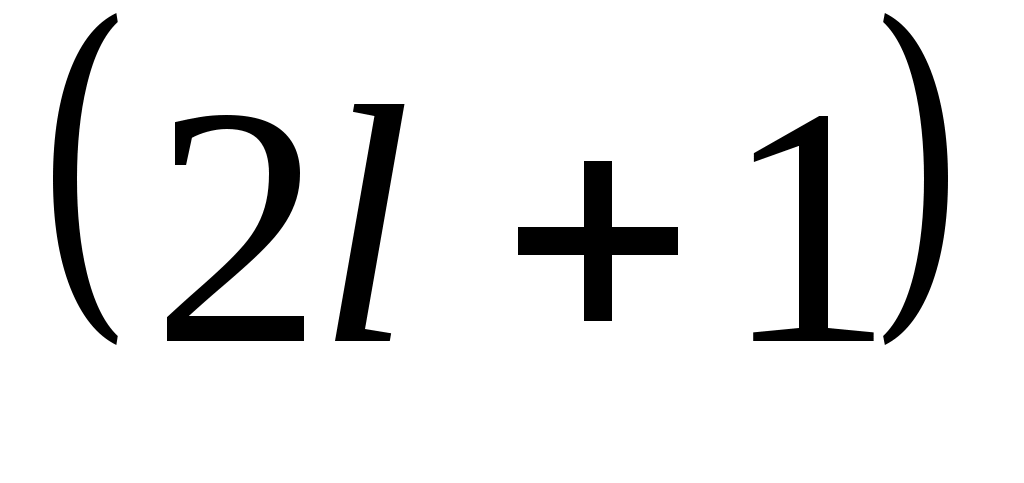 шамасы кванттық күйін азғындау еселігі деп аталады. шамасы кванттық күйін азғындау еселігі деп аталады.
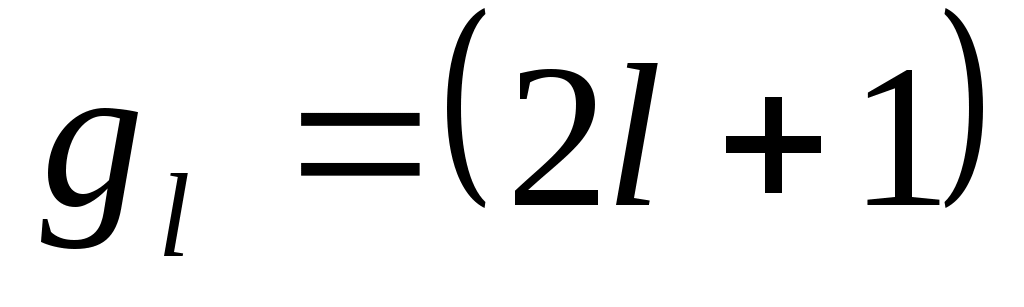 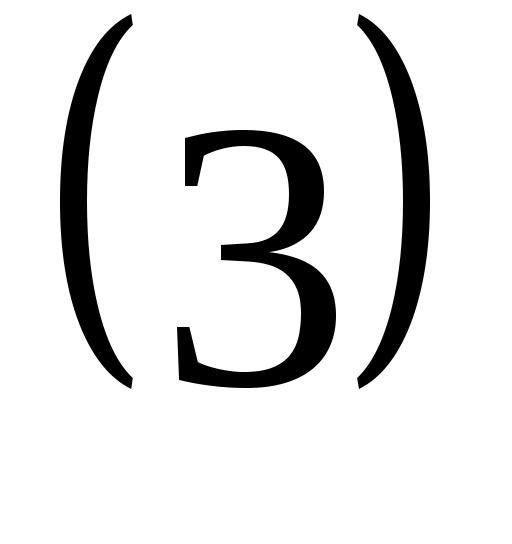
(2)-ші формуланы біз сіздермен ротатор энергиясын анықтауға қолданайық.
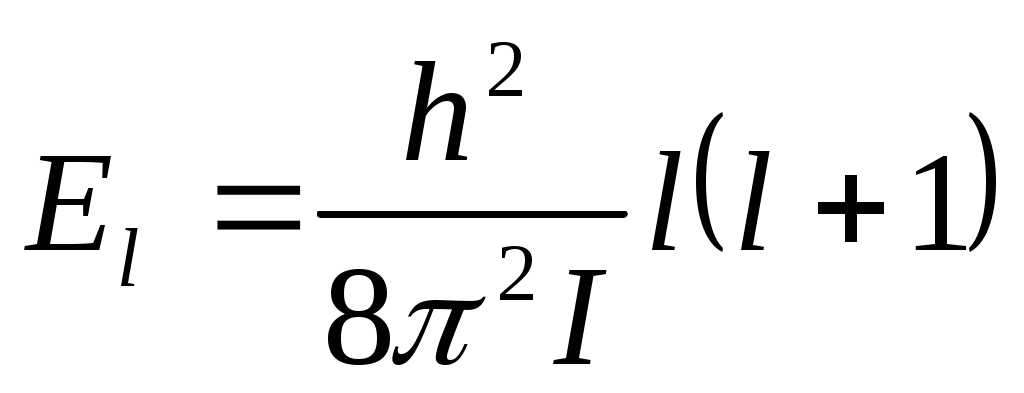 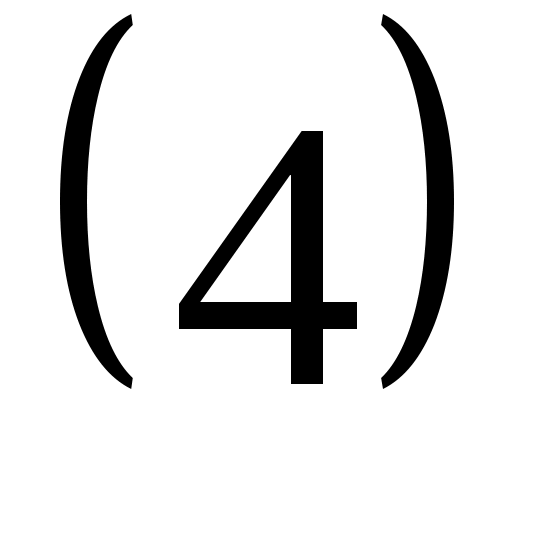
(4)- кванттық ротатордың энергиясы.
Ротатор жүйесінің статистикалық қосындысы
Статистикалық қосындыны есептеу үшін біз сіздермен стандарттық процедураны пайдаланамыз.Анықтамасы бойынша статистикалық қосынды деген ол келесі шама: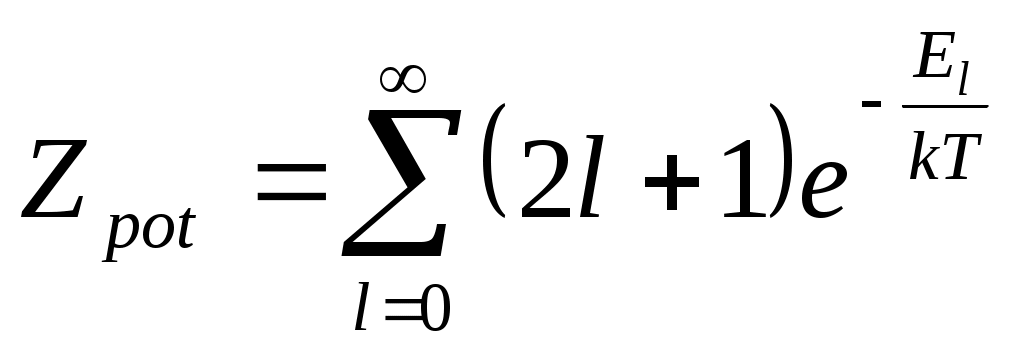 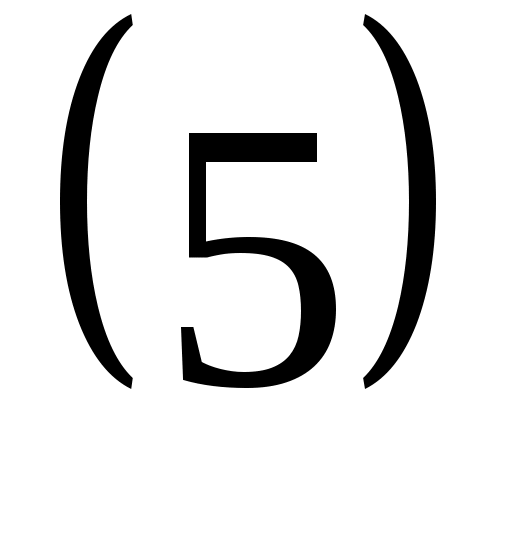
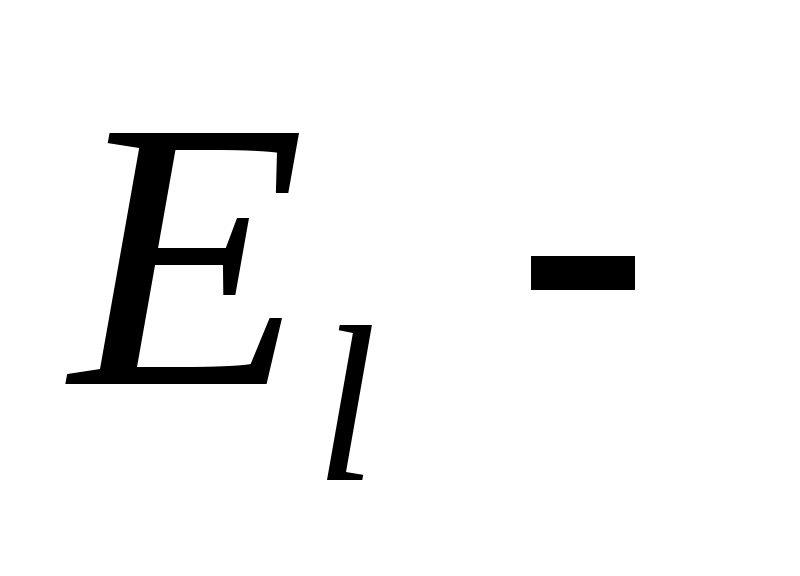 ротатордың энергиясы. ротатордың энергиясы. жалпы анықтама формуласы.Енді осыны есептейік. жалпы анықтама формуласы.Енді осыны есептейік.
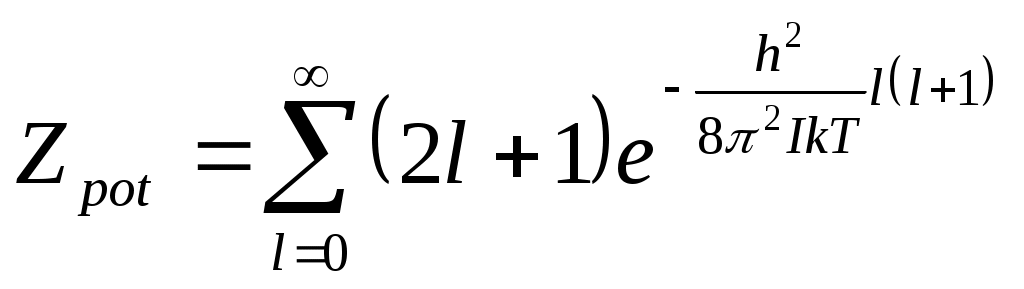 
Бұл кванттық ротатордың статистикалық қосындысы. шы формуланы өрнектейік.Ол үшін екі жағдайды қарастырайық. шы формуланы өрнектейік.Ол үшін екі жағдайды қарастырайық.
a)  болса, онда ротатордың қозғалысы баяу,энергиясы төмен болады.Сол себептен қозғалысты сипаттайтын сандар болса, онда ротатордың қозғалысы баяу,энергиясы төмен болады.Сол себептен қозғалысты сипаттайтын сандар 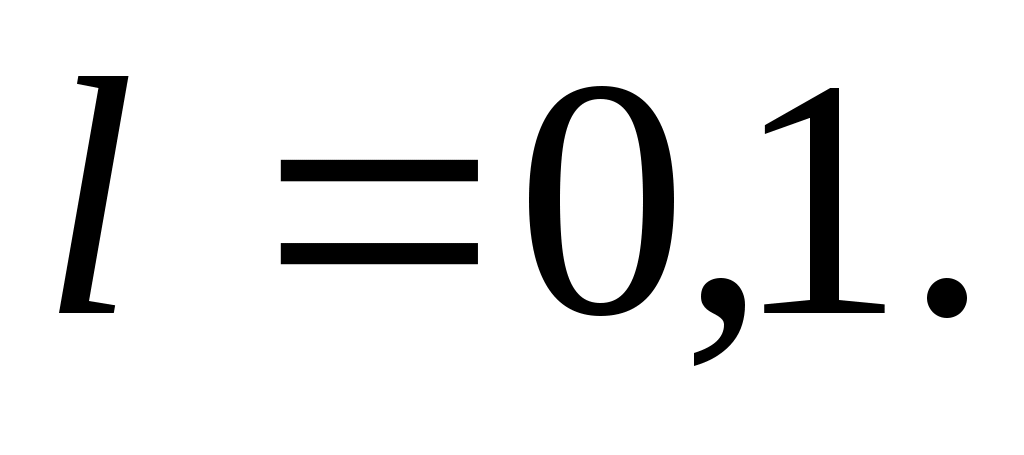 болады.Олай болса, болады.Олай болса,
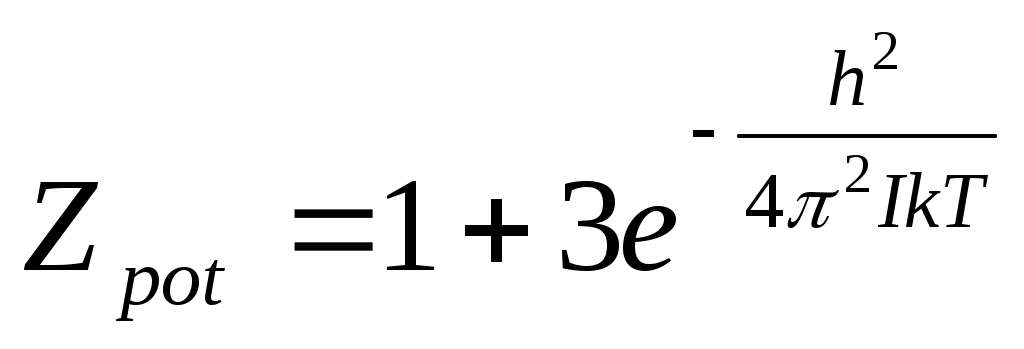 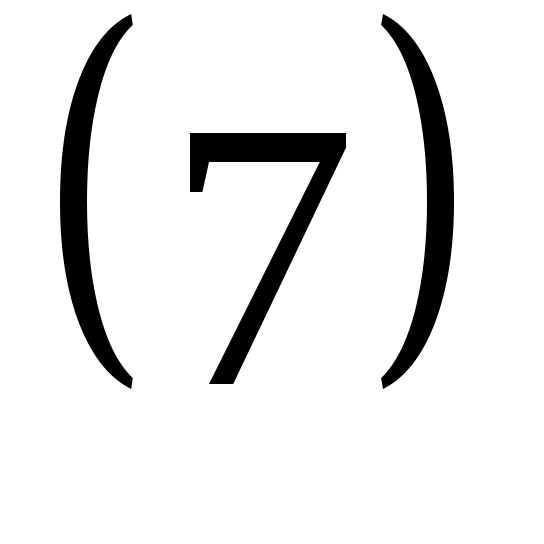
Үлесті жылу сыйымдылықты анықтау үшін ең бірінші энергияны анықтайық.
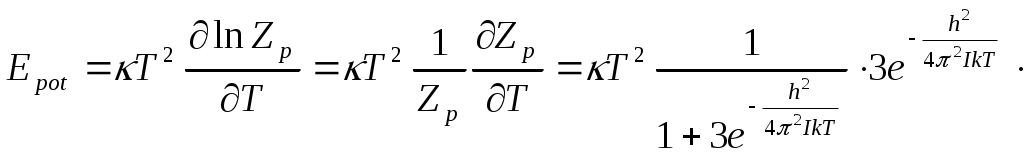 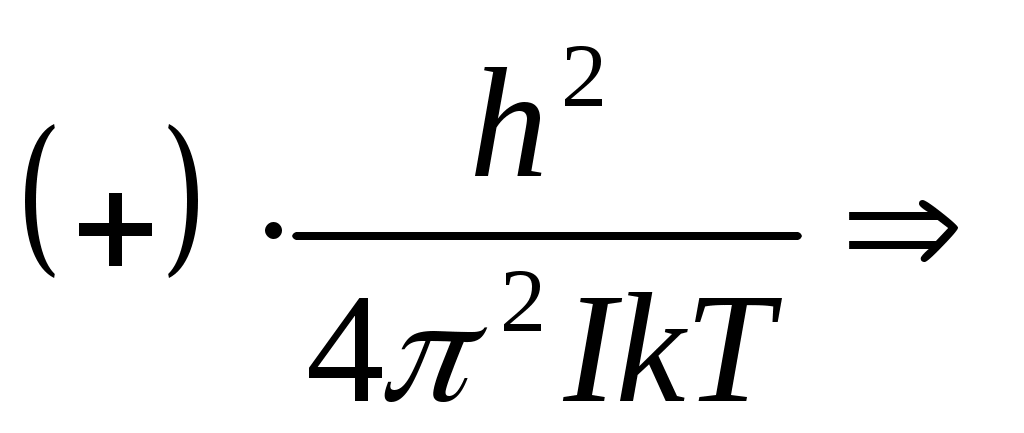
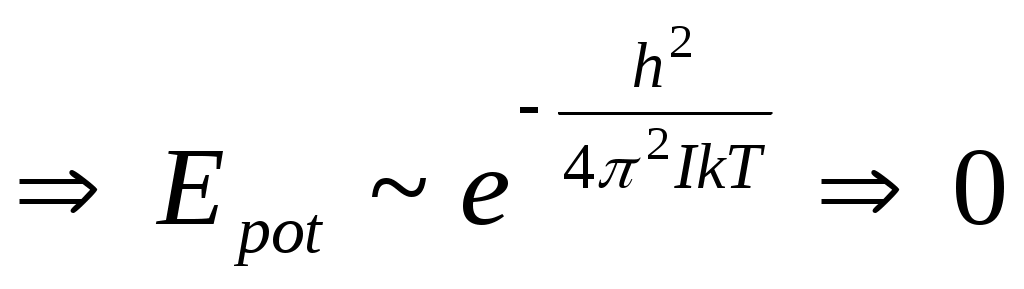
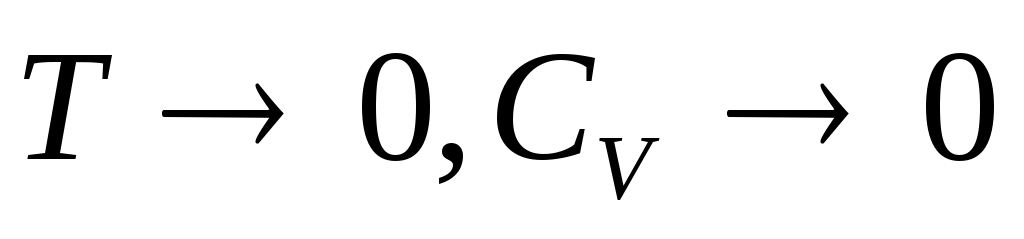 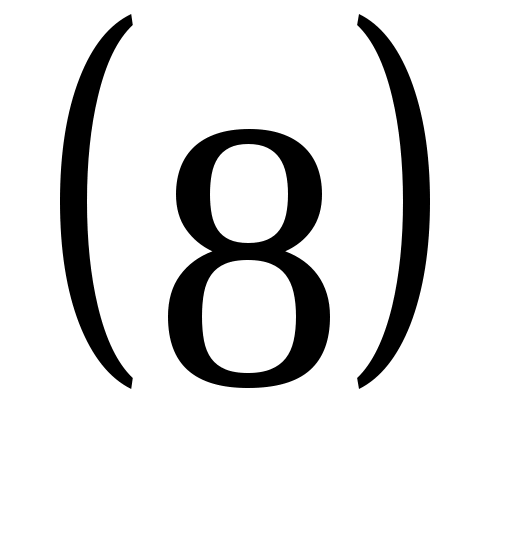 болады. болады.
б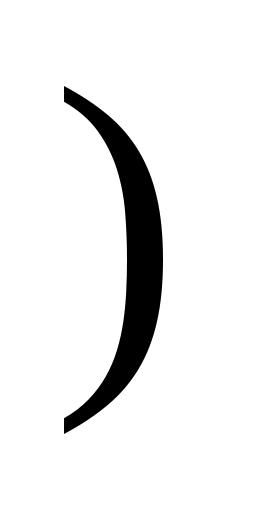 Т Т болса, орбитальдық кванттық санның l-і көп болады сол себептен біз (6) формулада қосынды процедурасын интегралдау процедурасына алмастырамыз. болса, орбитальдық кванттық санның l-і көп болады сол себептен біз (6) формулада қосынды процедурасын интегралдау процедурасына алмастырамыз.
Z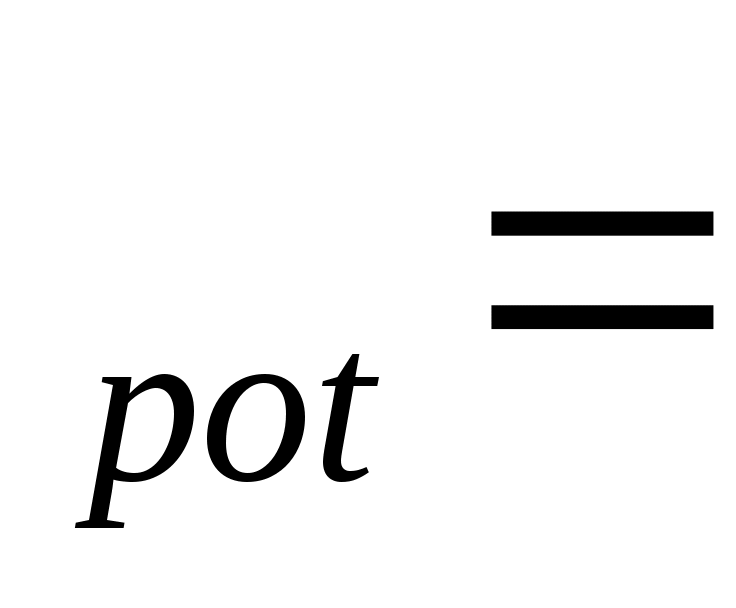 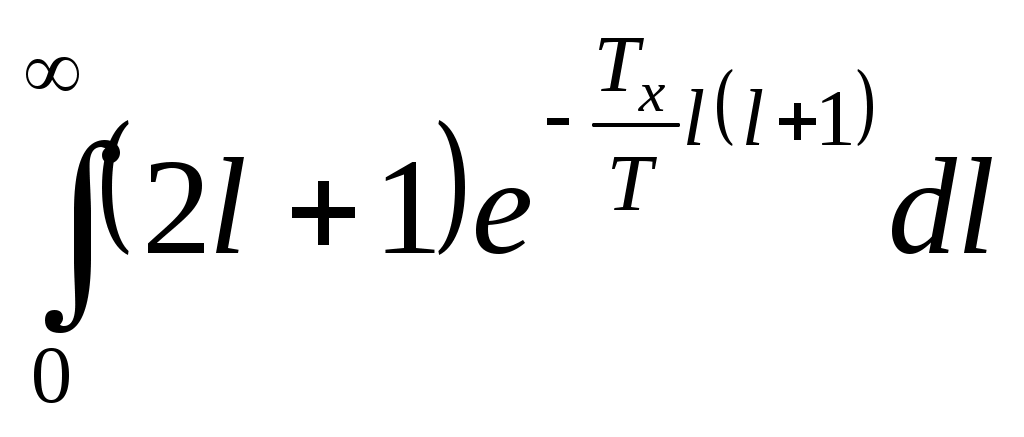 (10) (10)
T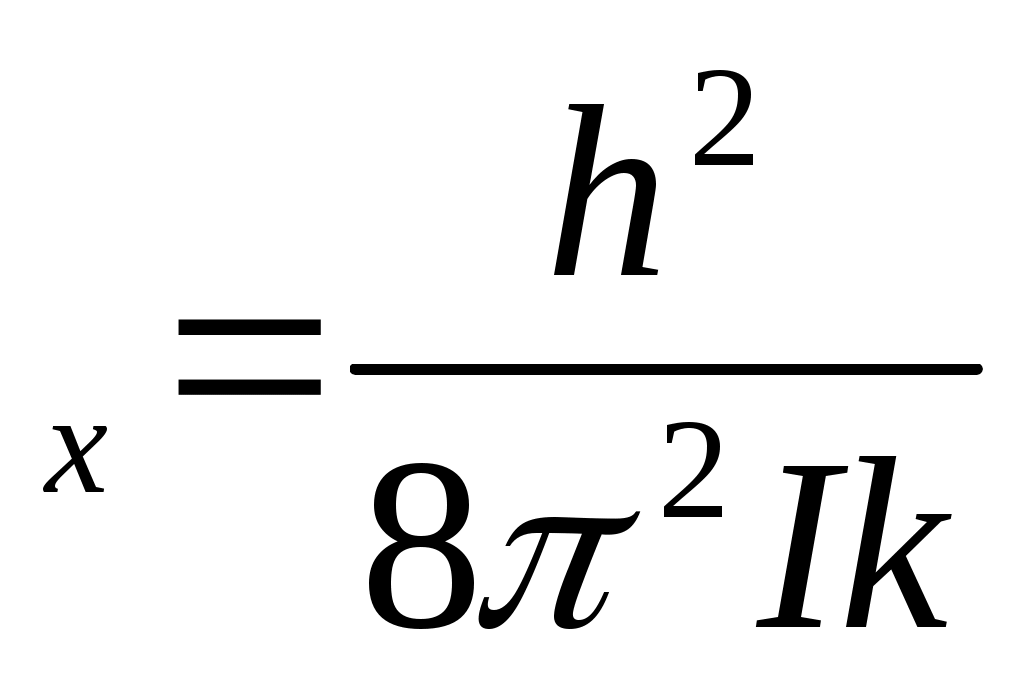  (9) (9)
T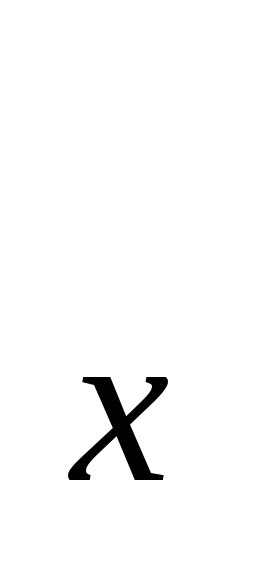 - рататордың параметрі - рататордың параметрі
(10) формуламен аңықталатын Z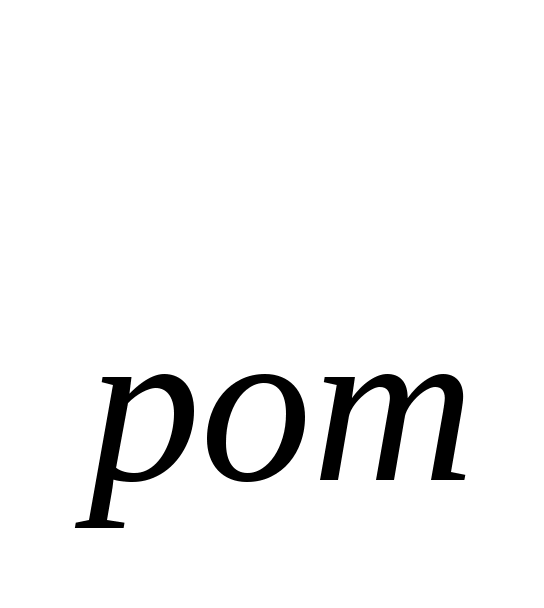 -ды есептеу. -ды есептеу.
Интегралдау процесін өткізу үшін дәрежелердегі шаманы басқа шамамен белгілейік.
Z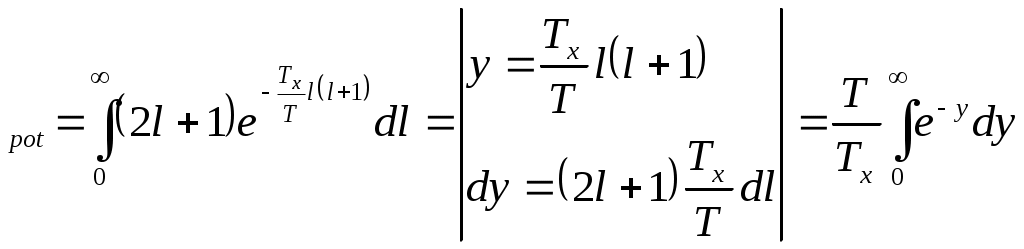 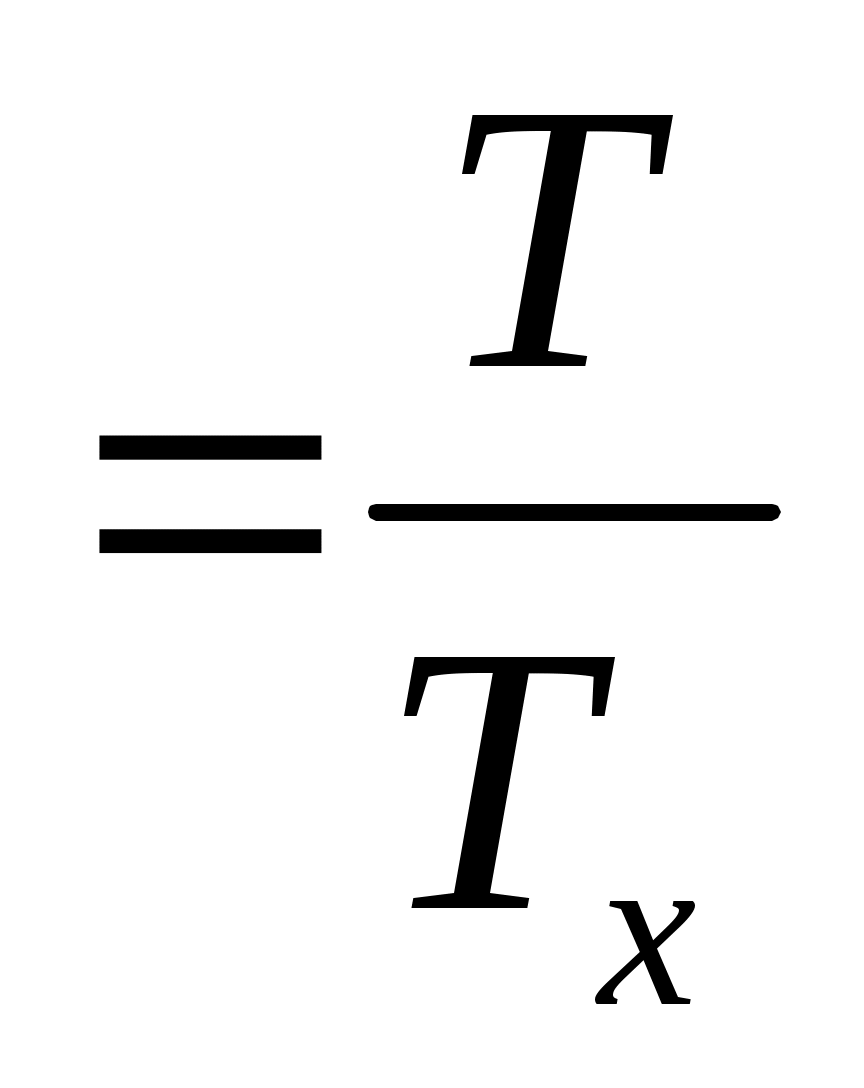 немесе немесе
 болса, болса, 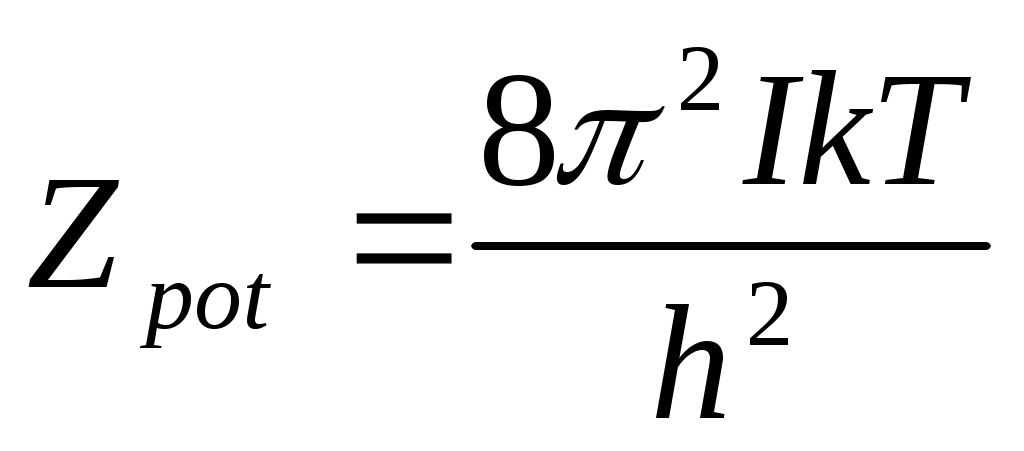 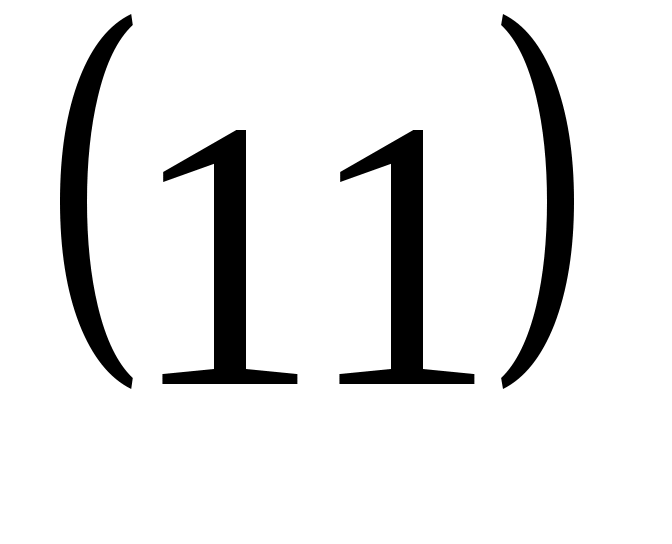
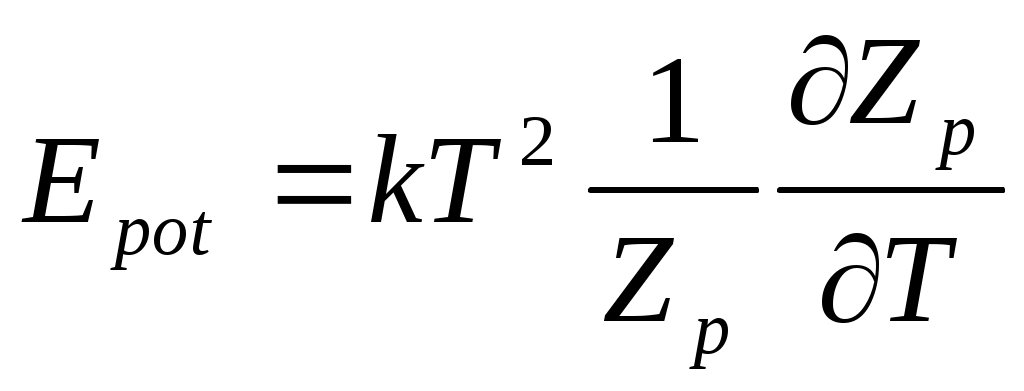
Алдымен бір ротатордың энергиясын анықтайық.
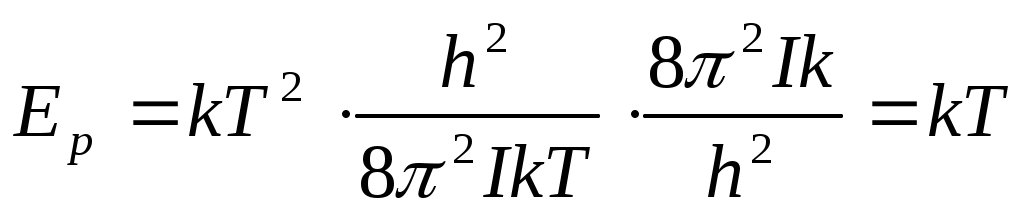
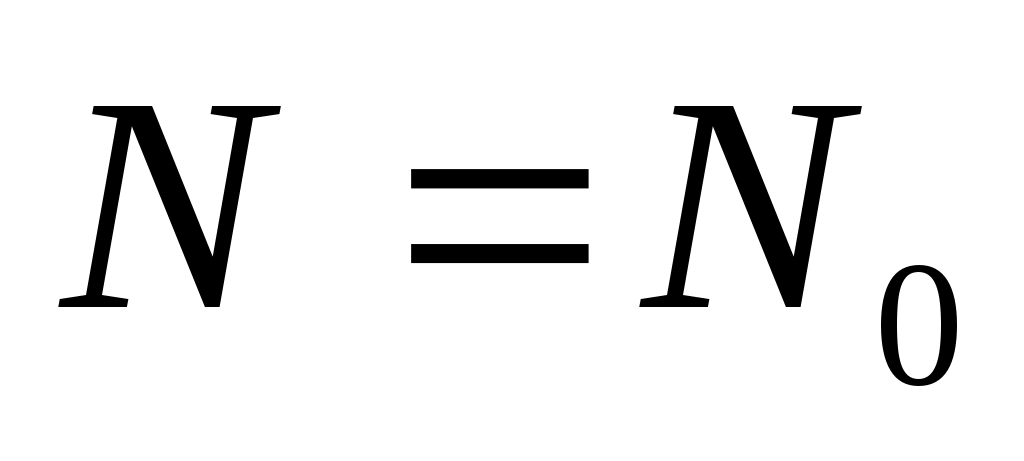  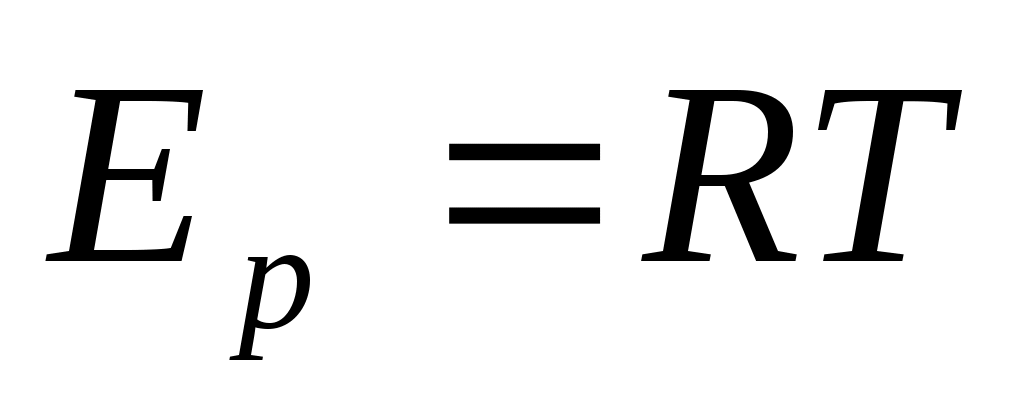 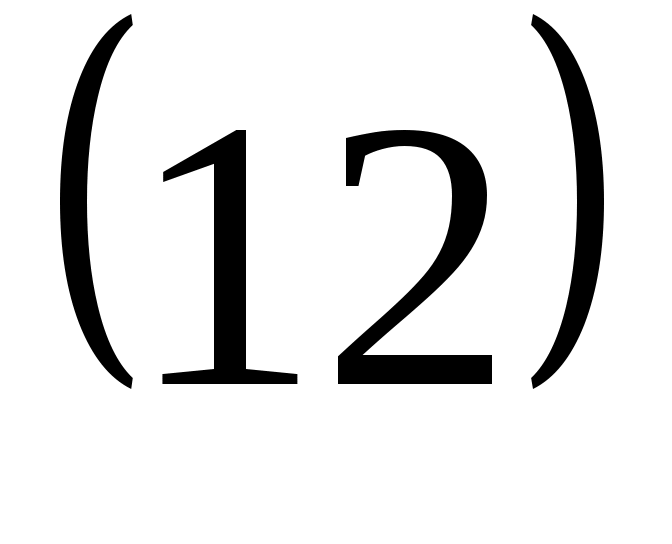
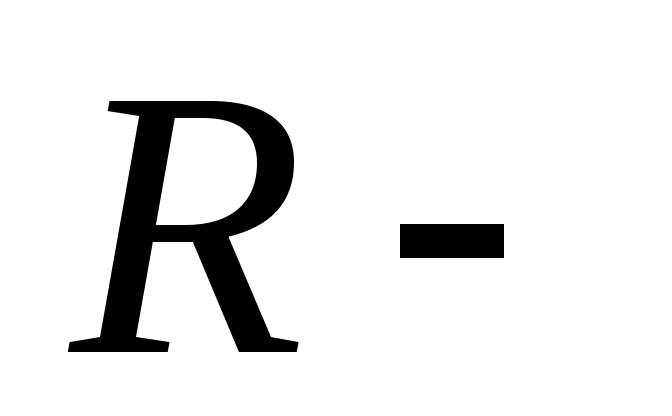 универсал газ тұрақтысы. универсал газ тұрақтысы.
Бұған сәйкес келетін үлесті жылу сыйымдылығы:
 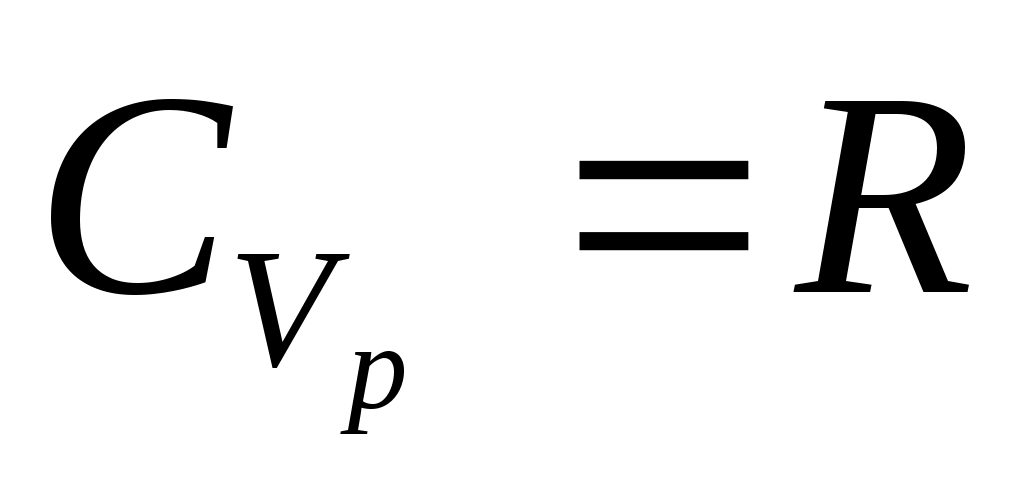 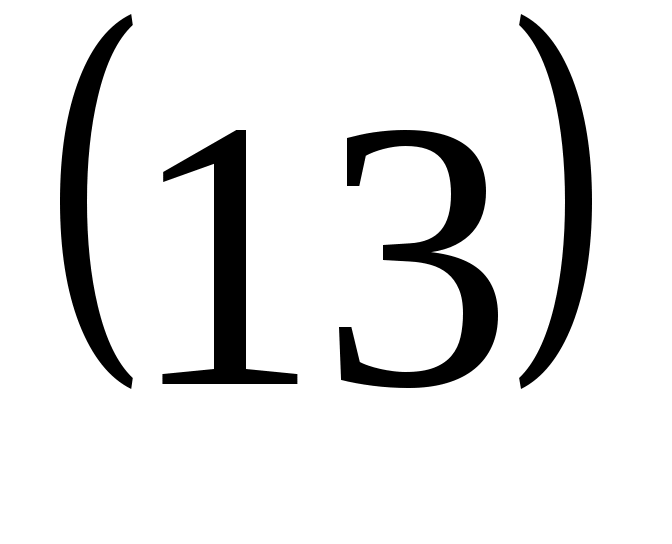

Нәтижесінде:
 , , 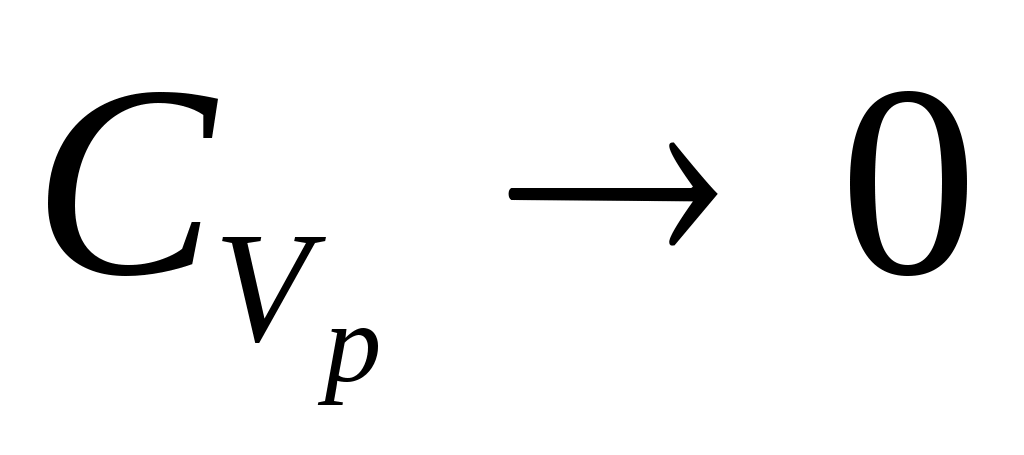
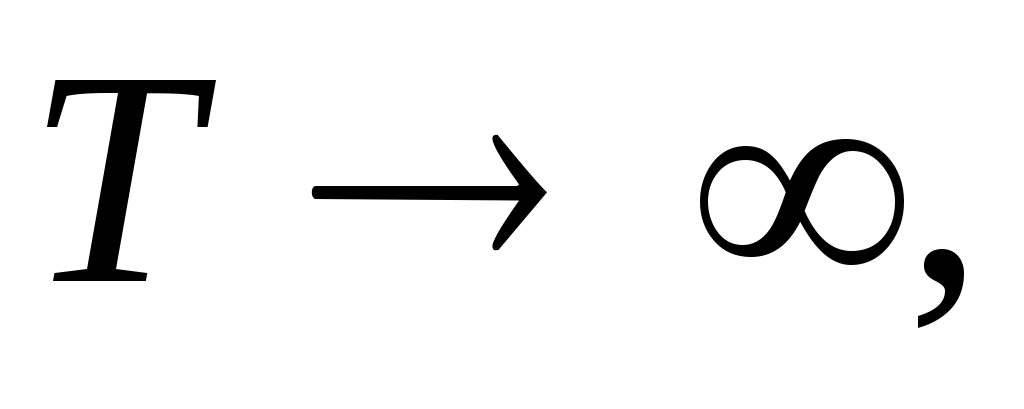 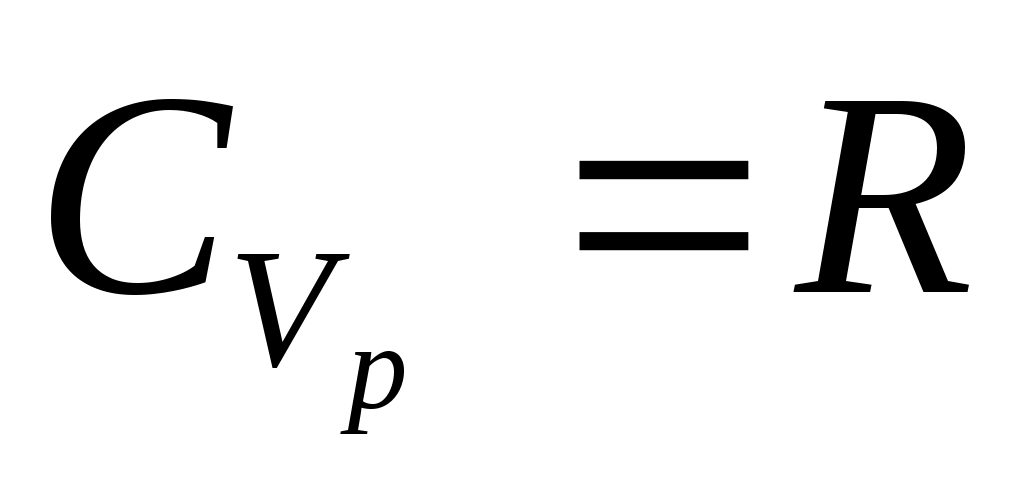
 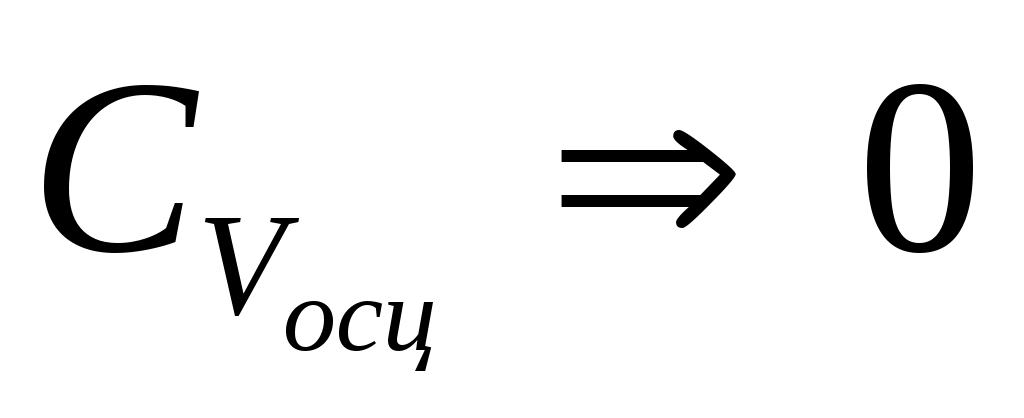
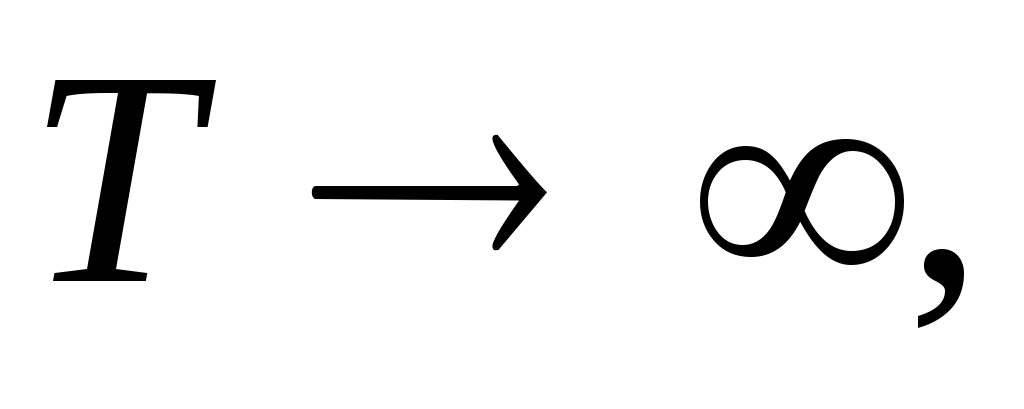 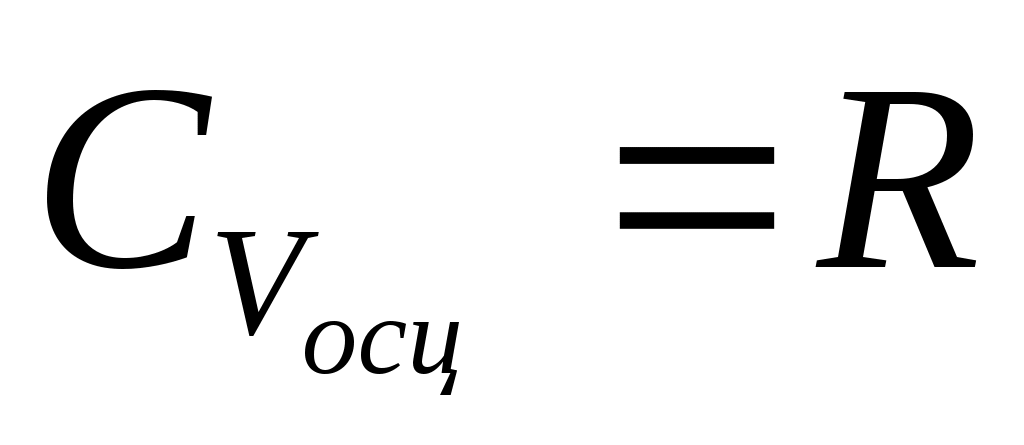
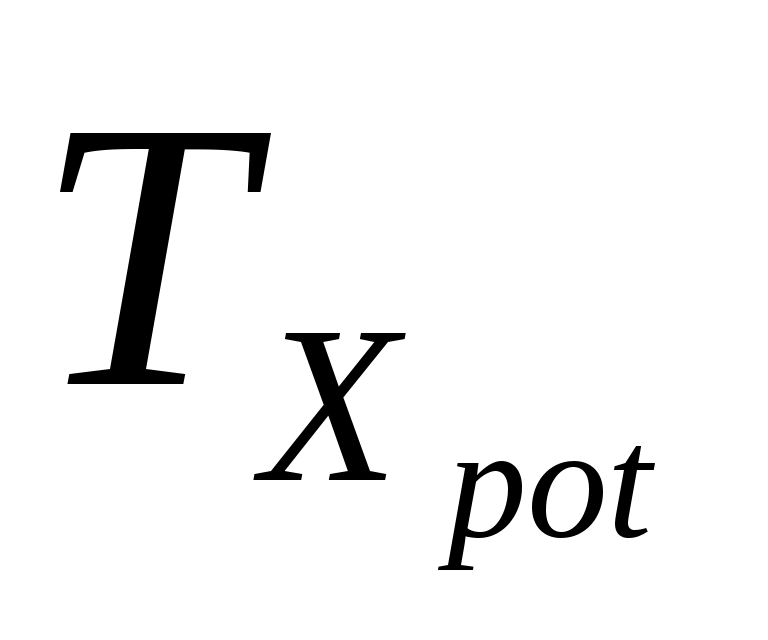
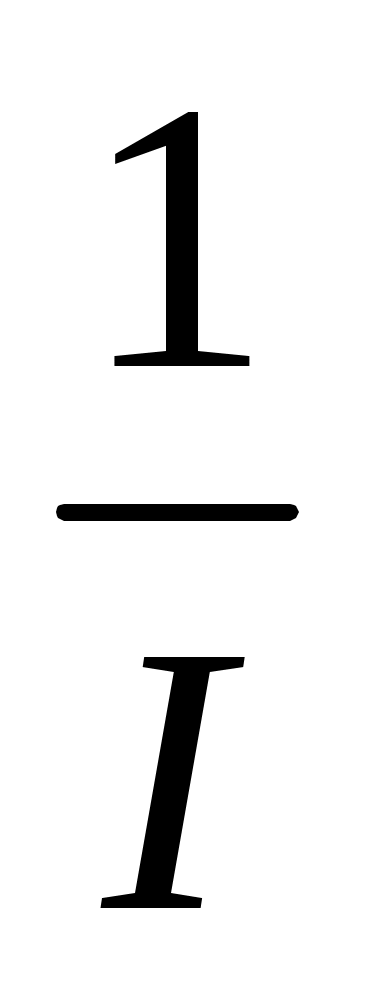
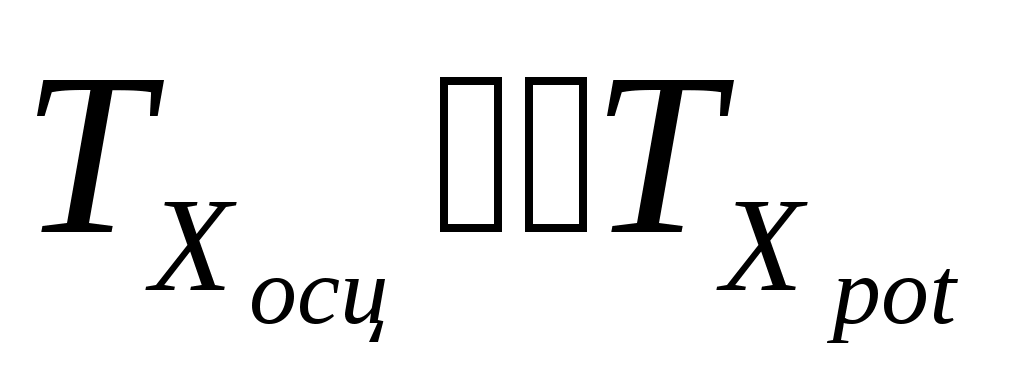
ГАЗ
|
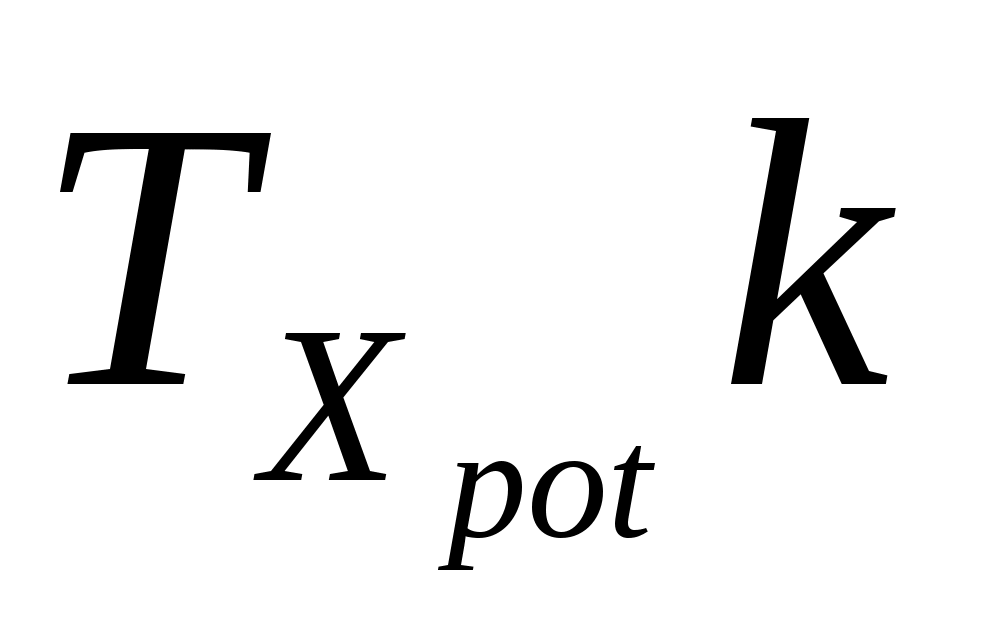
|
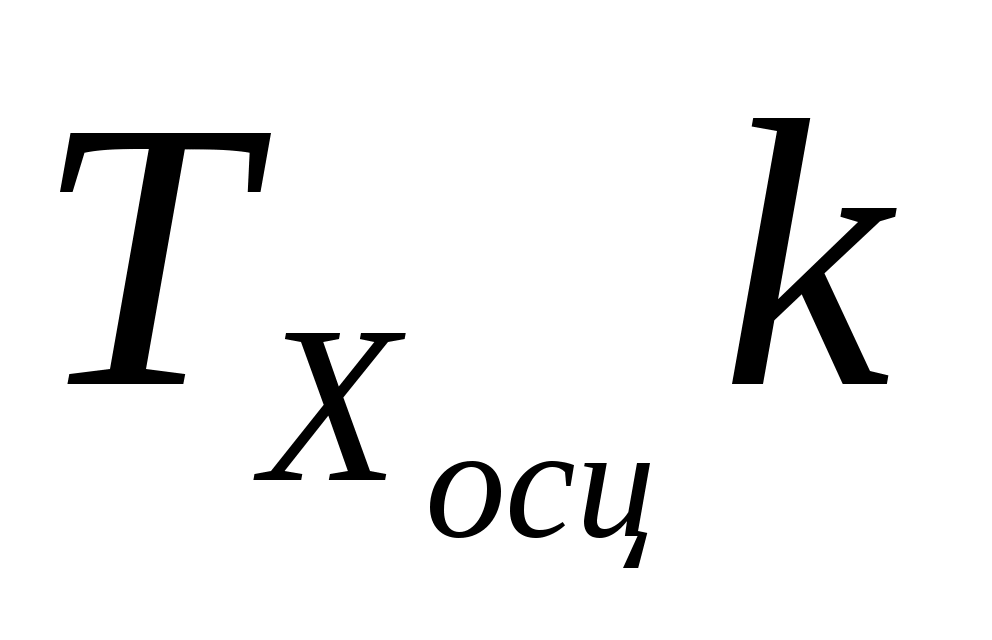
|
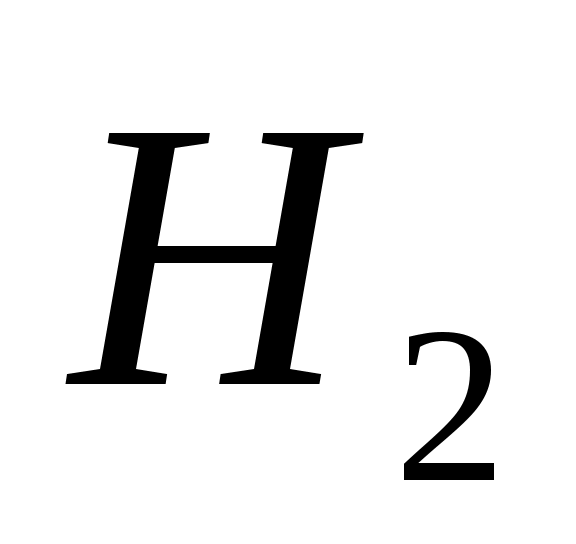
|
85,4
|
6000
|
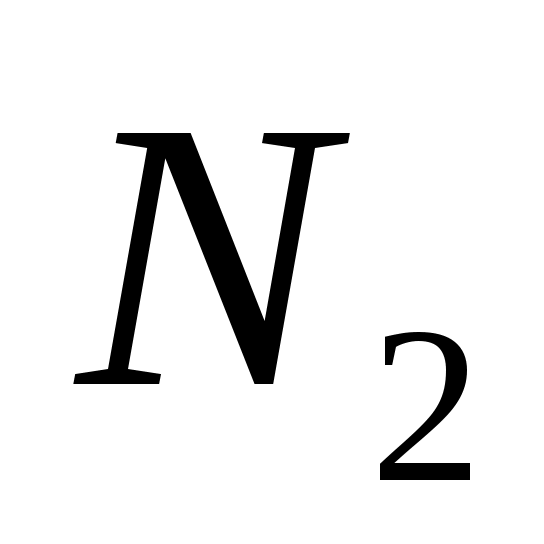
|
2,85
|
3340
|
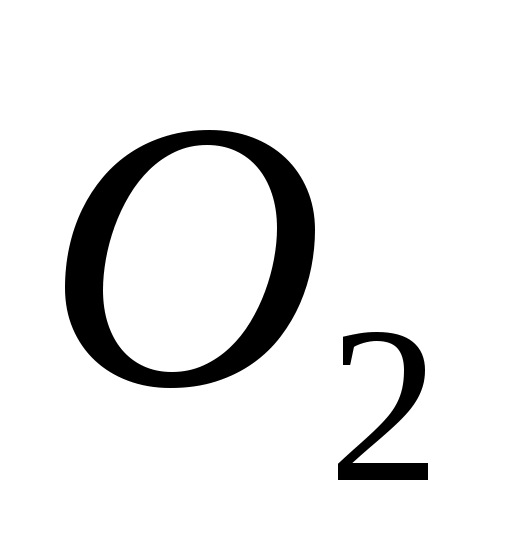
|
2,07
|
2230
|
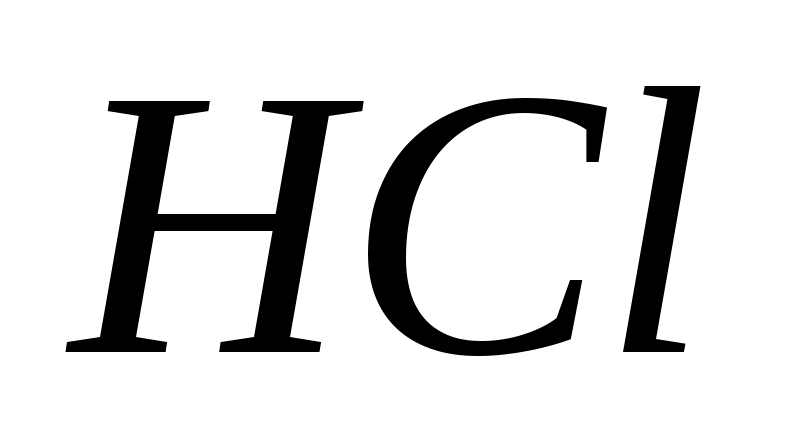
|
15,1
|
4140
|

|
9,0
|
3300
|
Берілген кестеге қарап , екі атомдық газдың үлесті жылу сыйымдылығының
Z-ке тәуелділігін анықтаймыз.
Екі атомды газдың үлесті жылу сыйымдылығының температураға тәуелділігі.
Екі атомдық молекулалардың толық энергиясы келесі теңдеу бойынша анықталады:
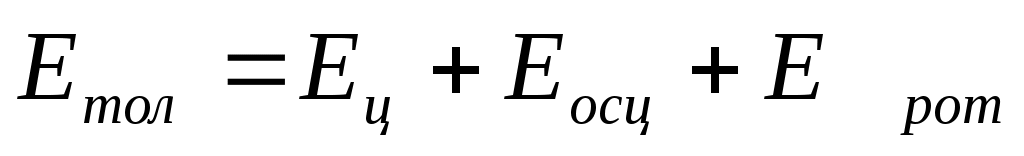 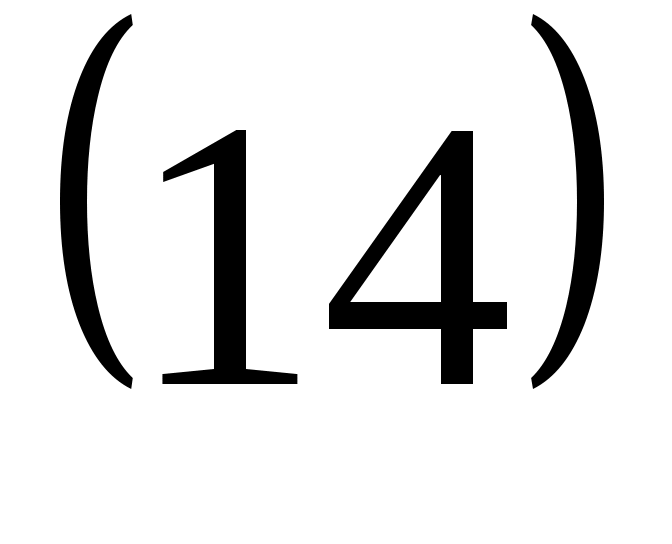
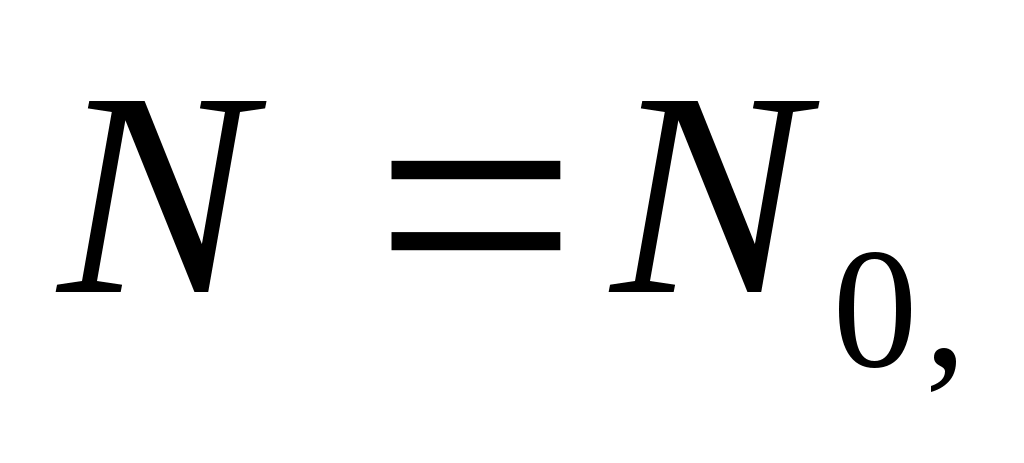  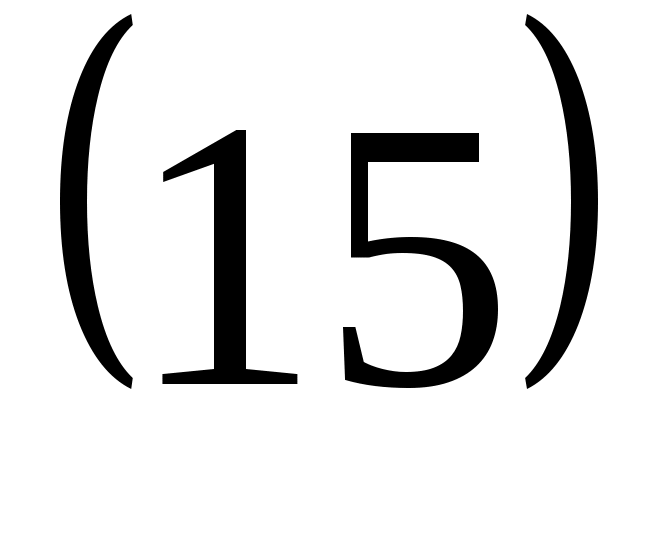
a)  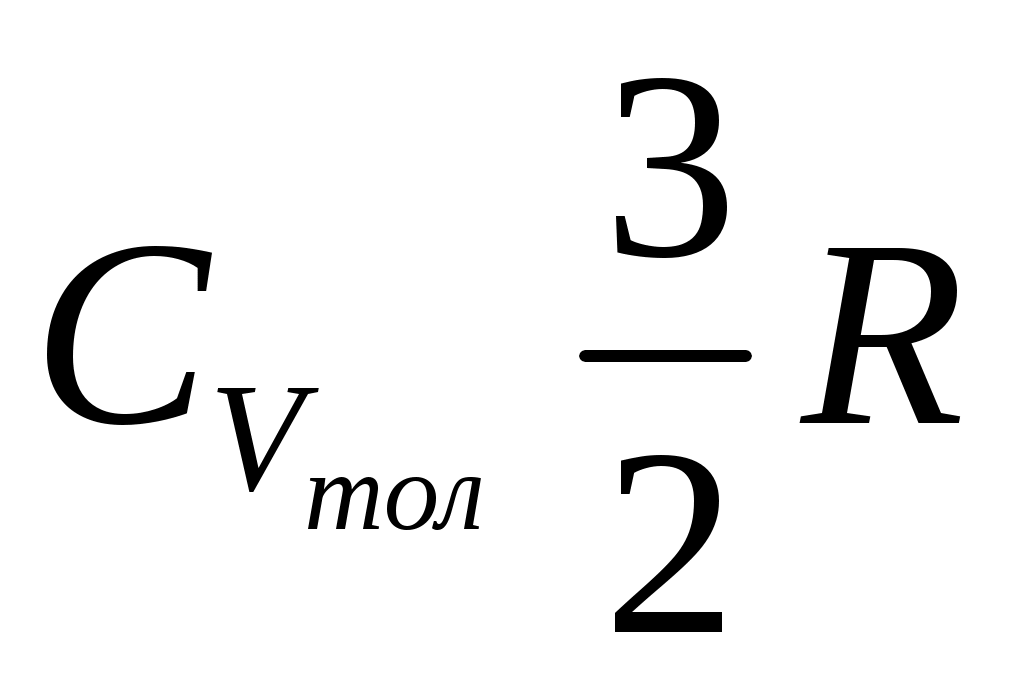 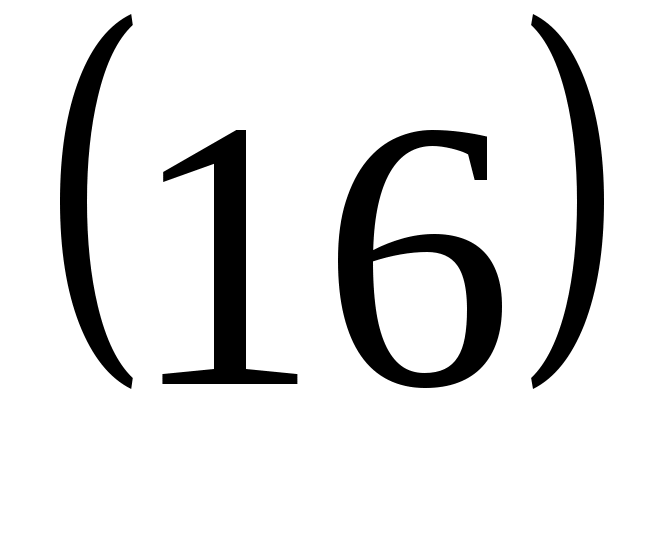
себебі: 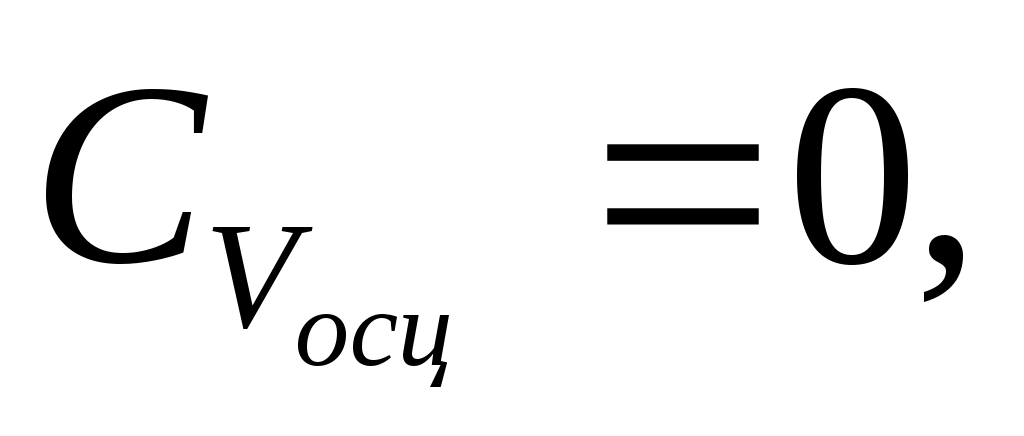 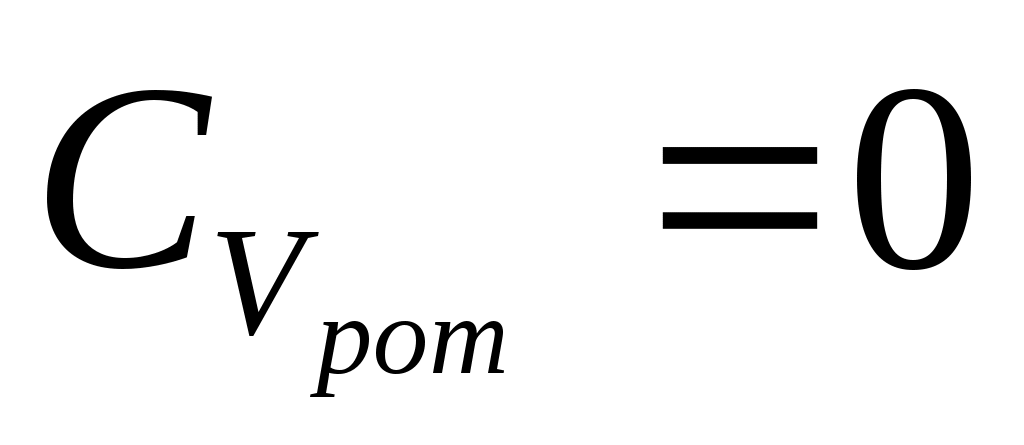
б) 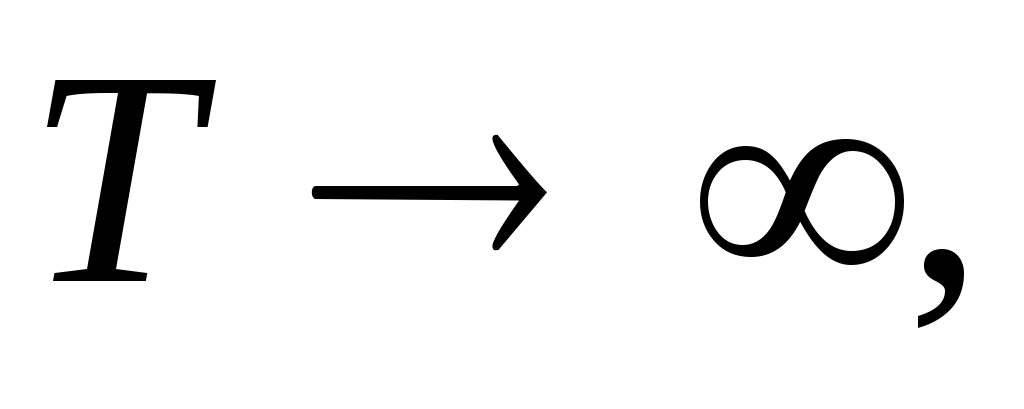 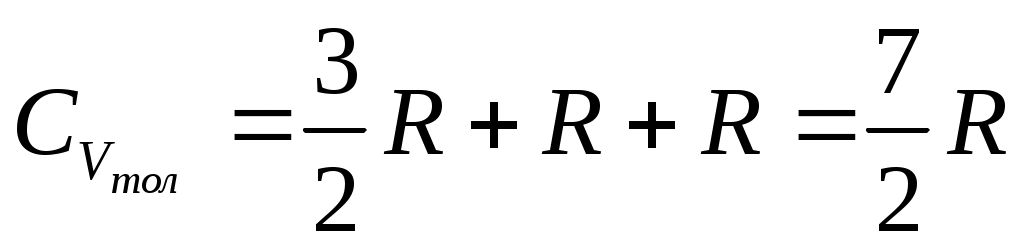
Енді біз осы нәтижені график түрінде келтірейік.

C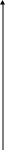 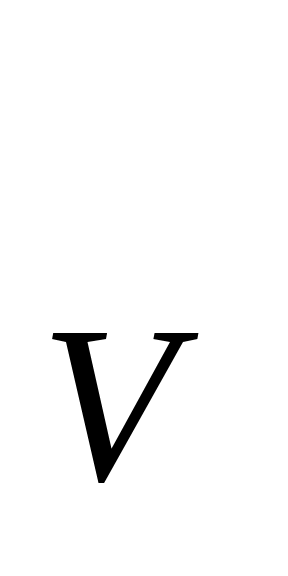 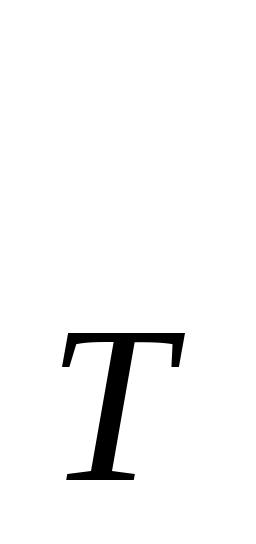
 4R 4R
 3R 3R

  2R 2R

 R R
    
 0 10 10 0 10 10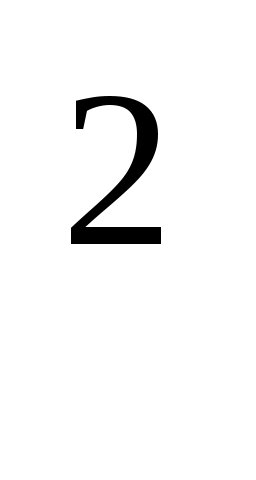 10 10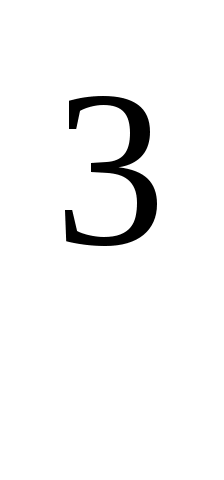 10 10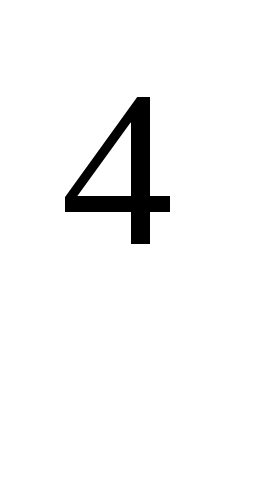 T T |
|
|
 Скачать 359.5 Kb.
Скачать 359.5 Kb.
 4R
4R
 3R
3R

 2R
2R
 R
R 




 0 10 10
0 10 10

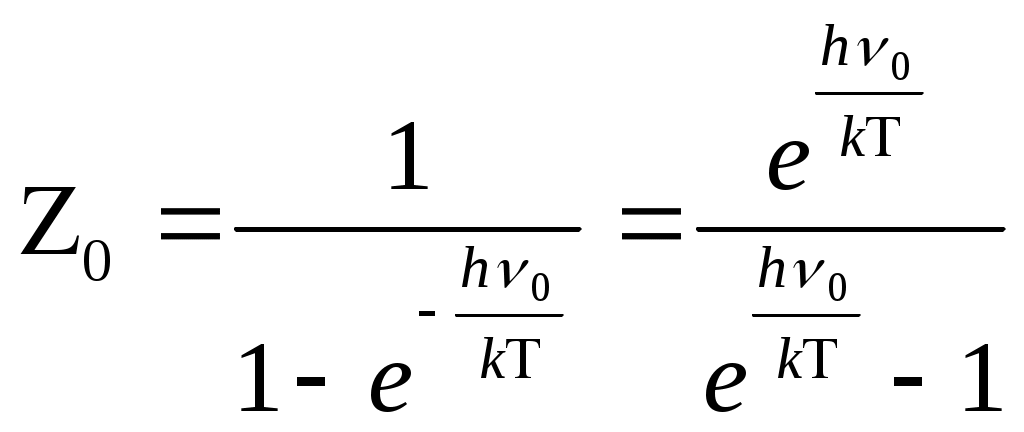 (2)
(2)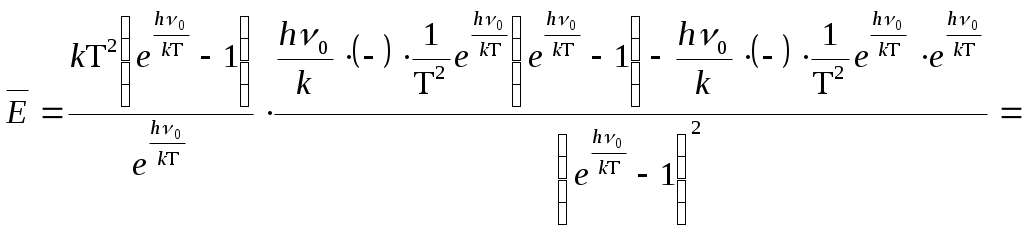
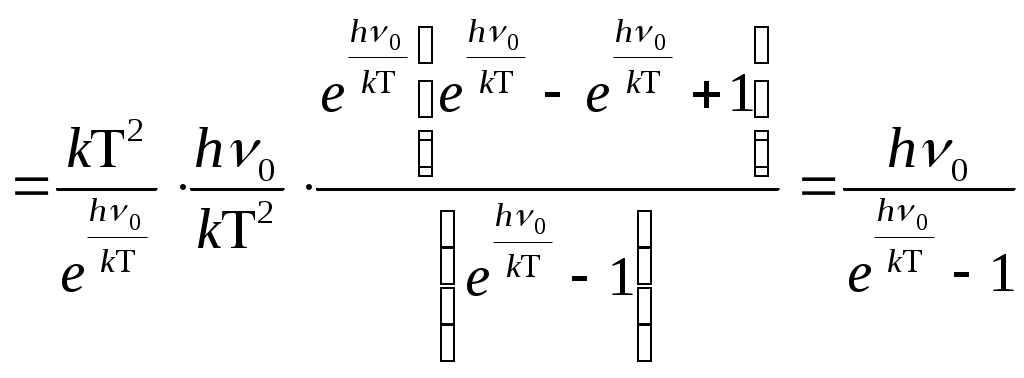
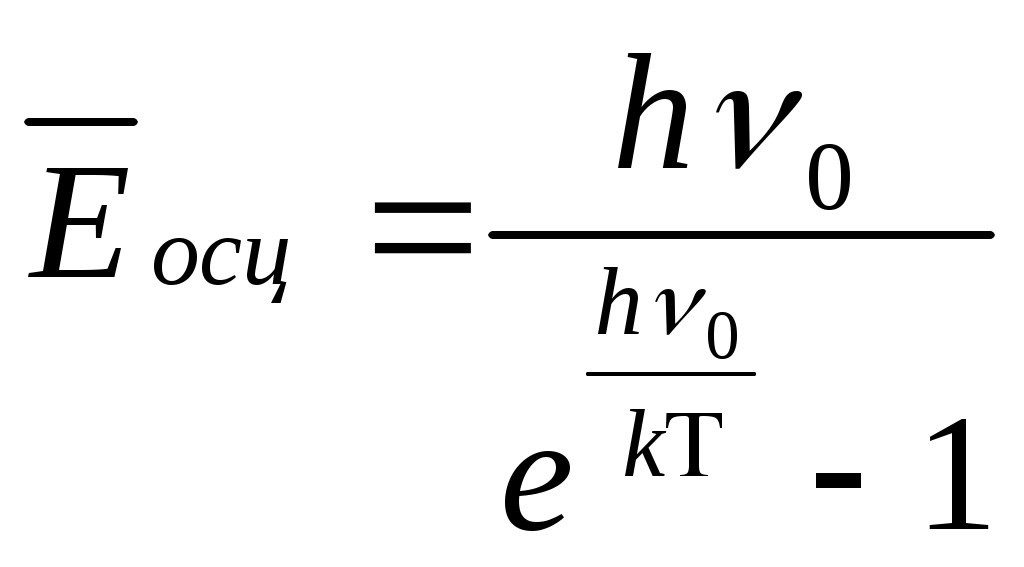 (3)
(3)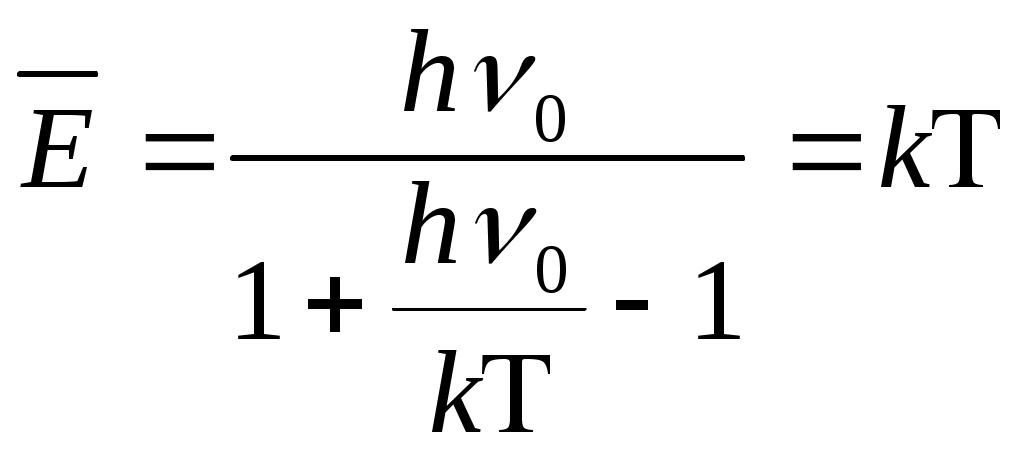
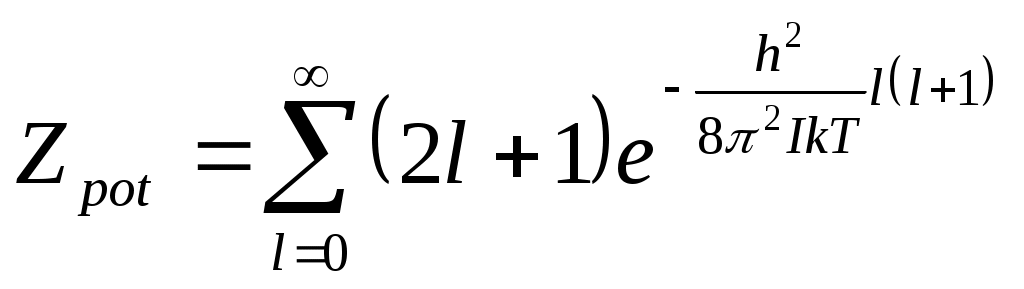
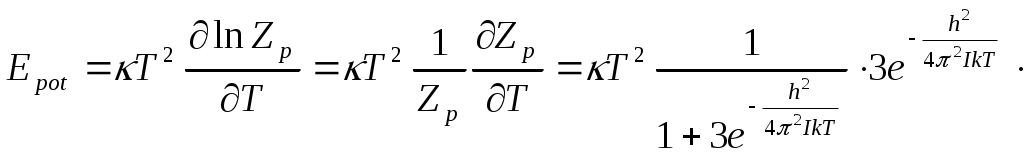
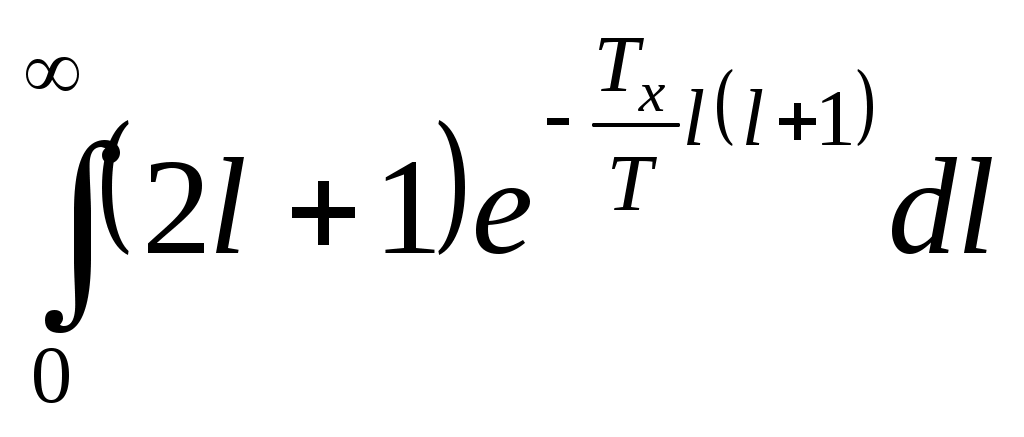 (10)
(10)