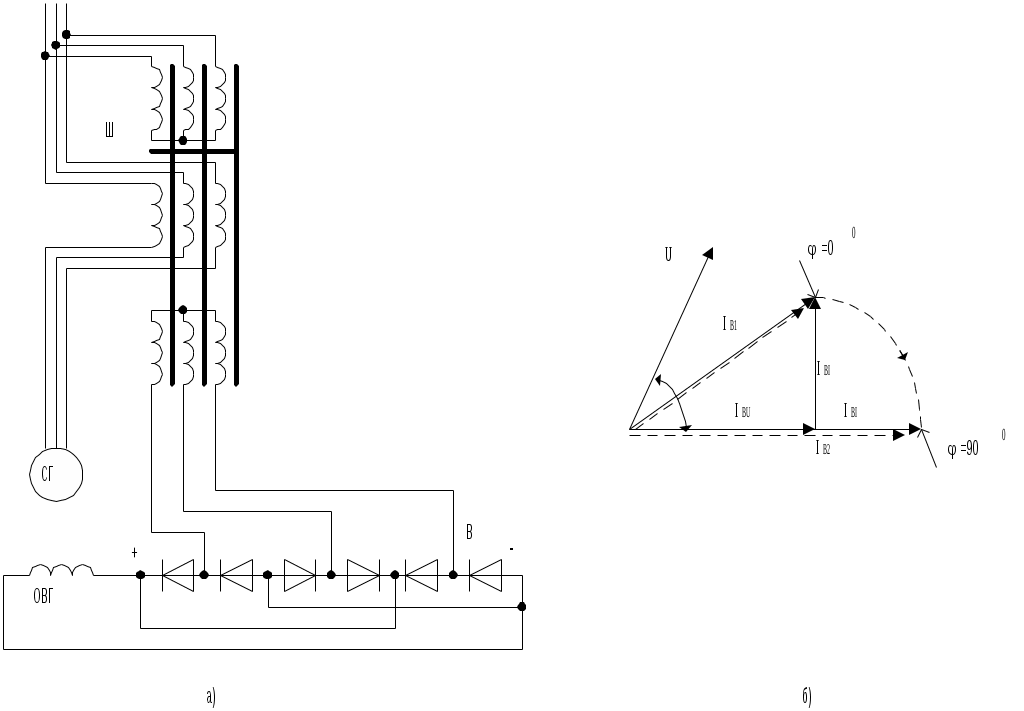Лекция 1. Судовые электроэнергетические системы. Лекция "Судовые электроэнергетические системы"
 Скачать 441.5 Kb.
|
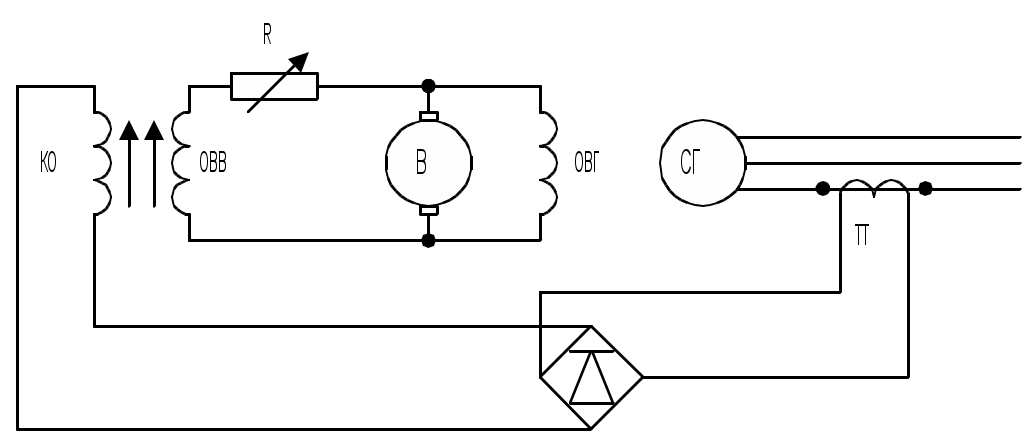
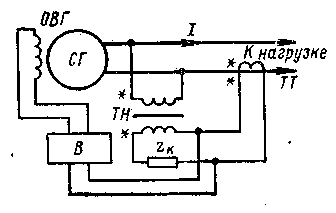
Лекция 1. "Судовые электроэнергетические системы"Введение Наиболее простым способом стабилизации напряжения СГ является компаундирование. 1. Системы автоматической стабилизации напряжения СГ, действующие по внешнему воздействию (системы компаундирования) Компаундирование – это введение дополнительного тока подпитки в обмотку возбуждения генератора (помимо тока, определяемого холостым ходом), пропорционального току нагрузки генератора. Величина этого тока должна быть такой, чтобы полностью скомпенсировать все факторы, снижающие напряжение генератора ниже номинального: - активное падение напряжения; - реакция якоря; - падение напряжения в добавочных полюсах. Компаундирование применяется как для машин переменного тока, так и для машин постоянного тока. Различают системы токового компаундирования, в которых ток возбуждения генератора определяется только значением тока нагрузки, и системы фазового компандирования, в которых ток возбуждения зависит как от значения тока нагрузки, так и от значения ее коэффициента мощности. Различают также системы прямого и косвенного компаундирования. Система косвенного компаундирования – это система, в которой управляющее воздействие осуществляется через возбудитель. Система токового компаундирования, являющаяся также системой косвенного компаундирования представлена на рис.11.1.
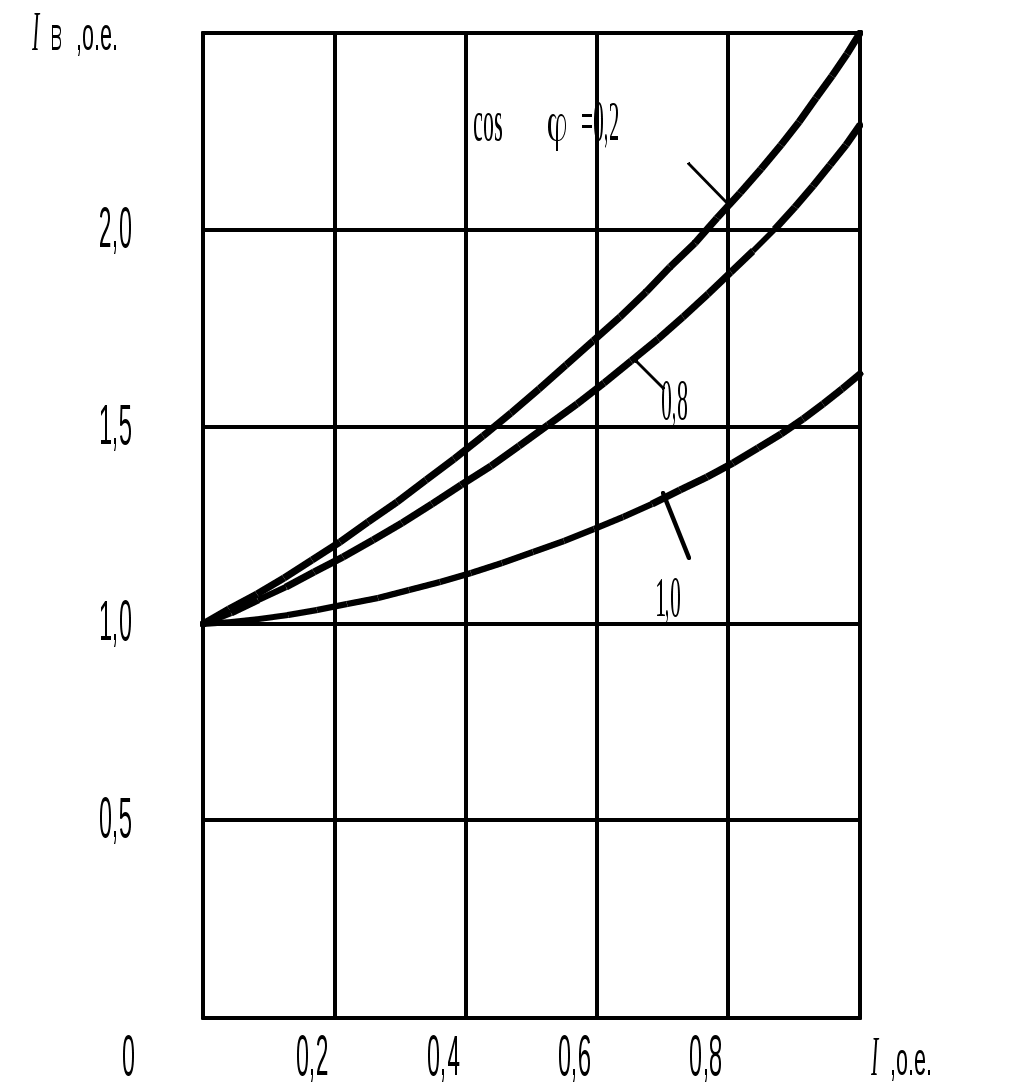
Основными элементами схемы, приведенной на рис.11.1, являются: управляемый объект – генератор СГ, управляющее устройство – возбудитель В, трансформатор тока ТТ с выпрямителем. Требуемое значение напряжения генератора в режиме холостого хода обеспечивается намагничивающей силой, создаваемой обмоткой самовозбуждения возбудителя ОВВ. Возрастание намагничивающей силы ротора с увеличением нагрузки достигается дополнительной компаундирующей обмоткой возбуждения КО, по которой протекает ток, пропорциональный току статора. Система прямого компаудирования – это системы, в которых управляющее воздействие производится непосредственно на цепь возбуждения генератора. В системах прямого компаундирования ток обмотки возбуждения СГ должен определяться двумя составляющими: составляющей напряжения генератора и составляющей тока его нагрузки. Составляющая тока ротора, пропорциональная напряжению генератора, необходима для обеспечения самовозбуждения машины; в этом нет принципиального отличия от самовозбуждающегося генератора постоянного тока. Составляющая тока ротора, пропорциональная току статора генератора, служит для компенсации всех факторов, снижающих напряжение машины при ее нагрузке. Однако точной компенсации при различных нагрузках, необходимой для поддержания заданного напряжения, в такой системе нельзя достигнуть из-за нечувствительности системы к изменению коэффициента мощности нагрузки, нелинейности характеристик генератора и возбудителя, колебаний частоты вращения и температурных влияний. По указанным причинам в системах токового компаундирования точность стабилизации напряжения недостаточна и ошибка составляет 5-10%. Для повышения точности стабилизации используют системы фазового компаундирования или комбинированные системы. Необходимость перехода к системам фазового компаундирования подтверждается следующими соображениями: напряжение СГ будет поддерживаться постоянным только в том случае, если ток возбуждения IВ будет зависеть от тока нагрузки I так, как это иллюстрируется семейством регулировочных характеристик генератора при различных cos (рис.11.2). Иначе говоря, если ввести понятие регулировочной (или выходной) характеристики системы прямого компаундирования (полагая под этим термином зависимость тока на выходе выпрямительных устройств, замкнутых на обмотку возбуждения, от тока нагрузки генератора при различных коэффициентах мощности, но постоянном напряжении), то точность стабилизации напряжения генератора во всех его нормальных режимах работы будет определяться тем, насколько близко совпадают регулировочные характеристики системы и генератора.
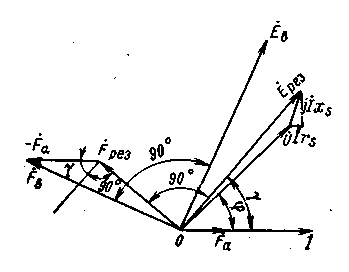
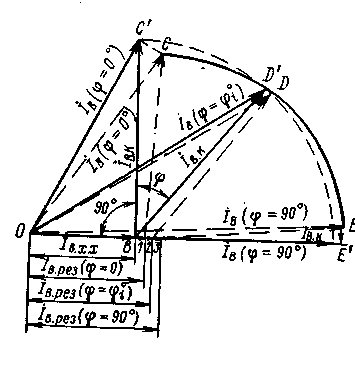
Прежде всего необходимо установить закономерность изменения тока возбуждения СГ, напряжение которого остается постоянным с изменением нагрузки и по значению и по коэффициенту мощности. Как известно, диаграмма Потье, строго справедливая для неявнополюсных машин, с достаточной для практических целей точностью может быть применена и для машин с явнополюсной системой возбуждения. Учитывая, что диаграмма дает наиболее наглядное решение вопроса о необходимом законе изменения тока возбуждения СГ при его нагрузке, рассмотрим ее построение для различных cos. На рис.11.3 представлена диаграмма Потье для генератора, нагруженного током Iпри коэффициенте мощности cos (>0).
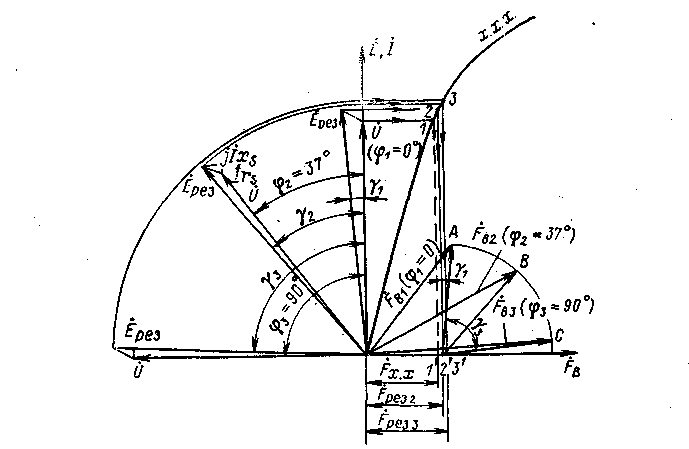
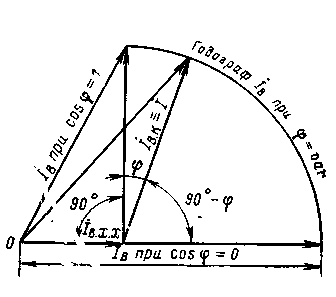
При построении диаграммы следует иметь ввиду, что для определения результирующей мдс обмотки возбуждения  необходимо из результирующей мдс геометрически вычесть мдс реакции статора  , причем угол между  и равен 900+, где - угол между вектором тока  и результирующей эдс машины  .Если совместить диаграмму Потье с характеристикой холостого хода (ххх) СГ и выполнить построения для различных cosφ (рис. 11.4), то можно установить, что годографом мдс обмотки возбуждения является кривая, весьма близкая к окружности, причем центр аппроксимирующей окружности расположен около конца вектора  , определяющего мдс в режиме холостого хода машины. Это позволяет заменить действительную диаграмму токов возбуждения СГ (рис. 11.5, а) приближенной (рис. 11.5, б), где ток возбуждения  машины определяется геометрической суммой двух составляющих: одна из них - ток возбуждения в режиме холостого хода  ; вторая, пропорциональная току нагрузки, в режиме φ=0 ортогональна первой, а при φ=90° совпадает с ней по направлению. В дальнейшем вторую составляющую будем именовать компаундирующей  . На рис. 11.5 совмещены обе диаграммы – действительная и приближенная, причем в последней компаундирующая составляющая (отрезки ВС'=BD'=BE') суммируется с током возбуждения в режиме холостого хода (ОВ) под углом 90°+φ.
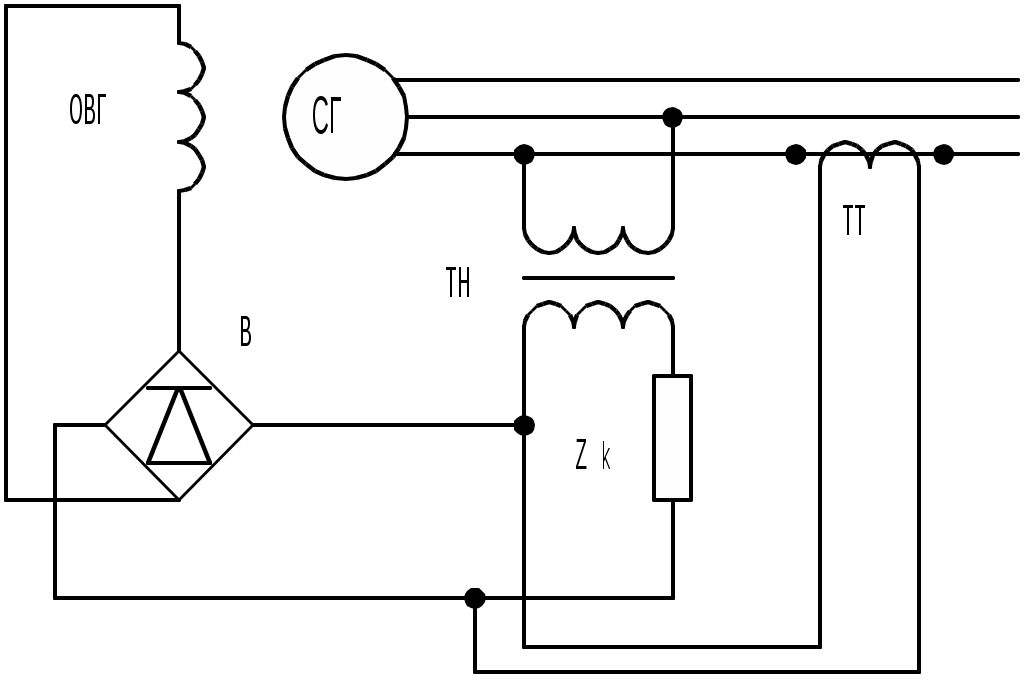
Погрешность, вызванная подобным представлением диаграммы токов возбуждения, зависит от параметров СГ. Таким образом, для того чтобы согласовать оба семейства регулироввочных характеристик – генератора и системы – и тем самым обеспечить стабилизацию напряжения при различных токах нагрузки и cosφ, необходимо геометрически суммировать величины, пропорциональные напряжению генератора и току его нагрузки (соответственно и ). Если суммировать эти величины арифметически, то ток возбуждения генератора не будет зависеть от коэффициента мощности нагрузки и согласованной окажется только одна пара регулировочных характеристик при определенном значении cosφ.Смотря по тому, как осуществляется суммирование величин, пропорциональных напряжению и току, - геометрически или арифметически, - различают соответственно системы прямого фазового компаундирования и прямого токового компаундирования. Принципиальная схема системы прямого фазового компаундирования (для однофазного генератора) представлена на рис. 11.6, где вторичные обмотки трансформатора напряжения ТН и трансформатора тока ТТ включены параллельно на вход выпрямителя В, нагрузкой которого служит обмотка возбуждения генератора ОВГ. Сопротивление zk в, цепи трансформатора ТН, называемое компаундирующим элементом, обеспечивает геометрическое сложение составляющих, пропорциональных напряжению и току. В приведенной схеме обмотки трансформатора ТН и ТТ соединены между собой до выпрямителя. Это позволяет произвести суммирование величин, пропорциональных U и I, геометрически, и ток возбуждения генератора при этом оказывается зависящим от коэффициента мощности нагрузки.
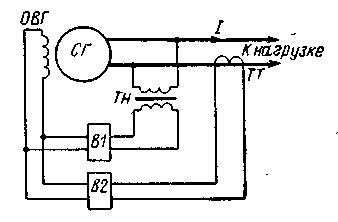
При арифметическом суммировании величин, пропорциональных напряжению и току генератора (токовое компаундирование), вторичные обмотки ТН и ТТ замыкают на два раздельных выпрямителя В1 и В2, включенных на общую нагрузку – обмотку возбуждения (рис.11.7). Естественно, что в данном случае ток возбуждения генератора от cosφ не зависит, а определяется лишь значениями напряжения и тока.
Системы фазового компаундирования стабилизируют напряжение с достаточно высокой точностью (статическая ошибка составляет 3-5%) и имеют в наличии только один блок выпрямления. Это является несомненным преимуществом фазового компаундирования по сравнению с токовым. 2. Компаундирующие сопротивления Существующие системы прямого амплитудно-фазового компаундирования могут быть классифицированы следующим образом: 1. схемы с электрическим суммированием составляющих; 2. схемы с электромагнитным суммированием составляющих. В свою очередь схемы с электрическим суммированием могут быть разбиты на две группы: 1. схема с параллельным соединением вторичных обмоток трансформаторов (рис.11.8); 2. схема с последовательным соединением вторичных обмоток трансформаторов (рис. 11.6).
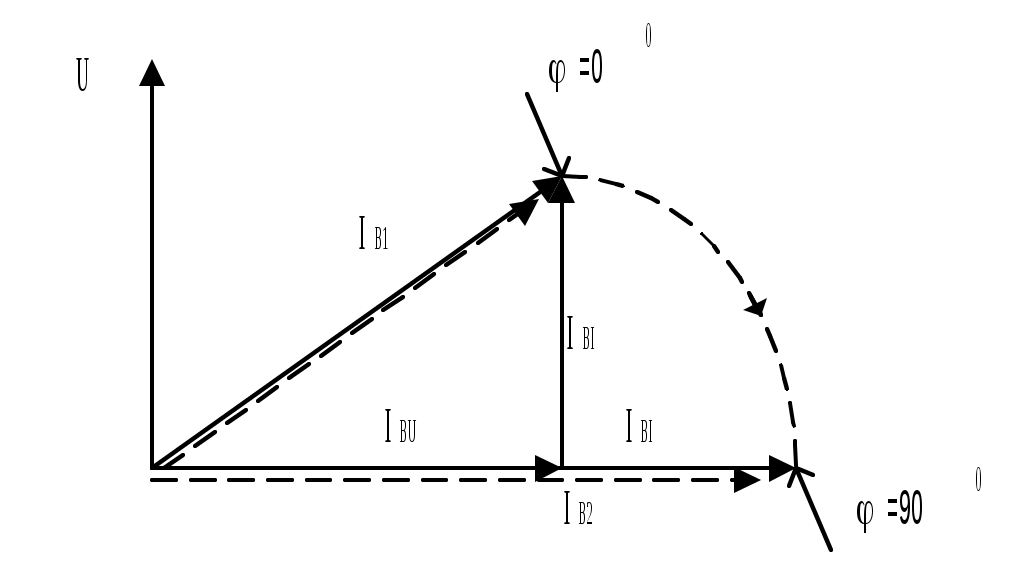
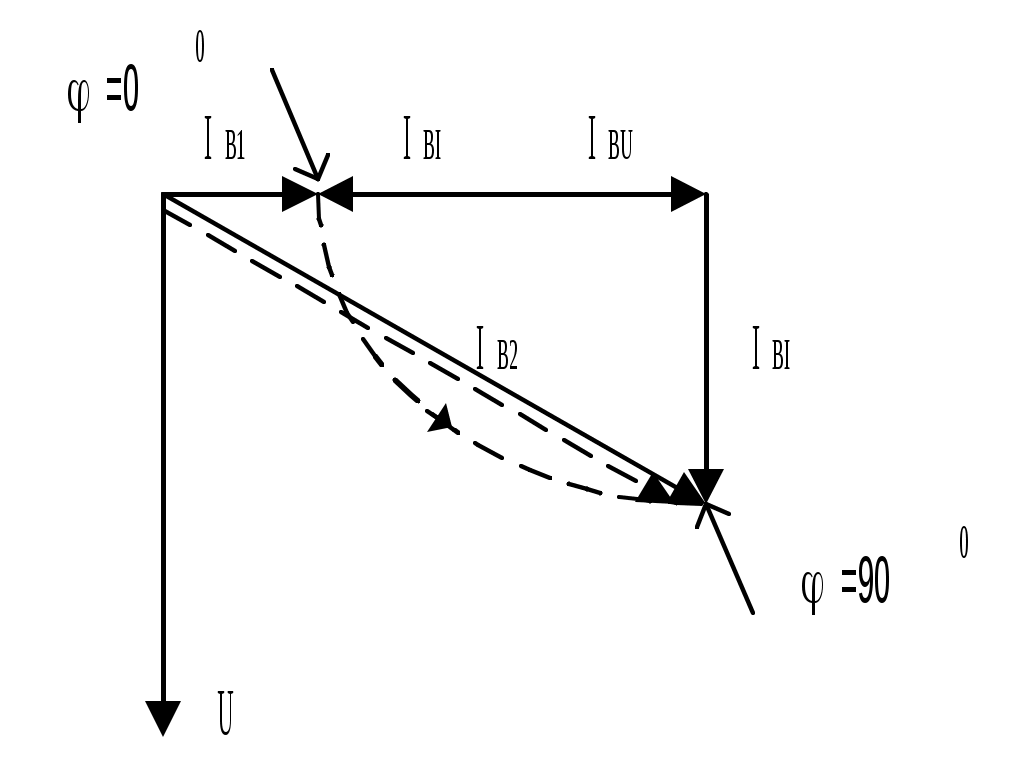
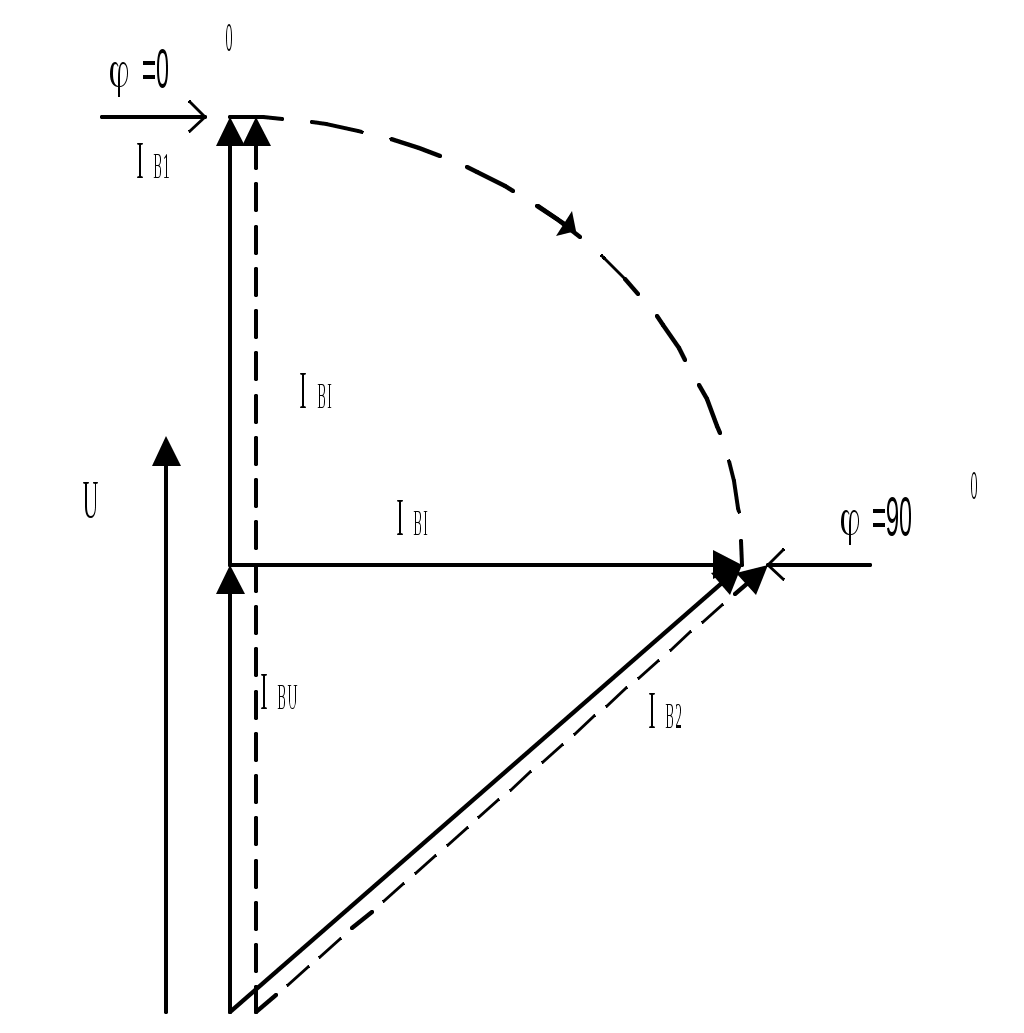
В системах амплитудно-фазового компаундирования решающее значение для получения требуемого характера изменения тока возбуждения имеет выбор компаундирующего сопротивления zк. Рассмотрим выбор компаундирующего сопротивления для первой схемы (рис.11.8). Если в этой схеме использовать в качестве компаундирующего элемента дроссель с малым активным сопротивлением (k=900), то при активной нагрузке (=00) угол между векторами IBU и IBI составит 900, а при индуктивной нагрузке (=900) угол между этими векторами будет 00. В первом случае ток возбуждения минимальный, во втором – максимальный (рис.11.9,а).
При 00< <900 вектор тока возбуждения занимает промежуточное значение. Схема обеспечивает амплитудно-фазовое компаундирование. Если использовать в качестве компаундирующего элемента конденсатор (k=-900), то при активной нагрузке (=00) угол между векторами IBU и IBI по-прежнему составит 900, но при индуктивной нагрузке (=900) этот угол составит 1800, то есть суммарный ток возбуждения упадет (рис.11.9, б). Очевидно, схема будет работать нормально, если при использовании в качестве компаундирующего сопротивления конденсатора переключить выходные зажимы вторичной обмотки ТТ. Если в качестве компаундирующего элемента использовать активное сопротивление (k=00), то при активной нагрузке (=00) составляющие тока возбуждения складываются арифметически, а при индуктивной нагрузке (=900) – геометрически под углом 900 (рис.11.9, в). Это означает, что изменения тока возбуждения при изменении характера нагрузки будут обратным требуемым. Рассмотрим выбор компаундирующего сопротивления для второй схемы (рис.11.9,б). Поскольку вторичная обмотка ТТ обладает большим индуктивным сопротивлением, то при активной нагрузке составляющая тока возбуждения от ТН, т.е. IBU будет отставать на 900 от составляющей тока возбуждения от ТТ, т.е. IBI. Вторичная обмотка ТТ выполняет роль компаундирующего дросселя, и потому получим требуемый характер суммирования векторов IBU и IBI (рис.11.9). Однако вследствие большой величины сопротивления вторичных обмоток ТТ составляющая тока возбуждения по напряжению практически равна нулю. Поэтому необходимо либо выполнять ТТ с воздушным зазором, чтобы увеличить рассеяние и уменьшить индуктивное сопротивление ТТ, либо шунтировать вторичную обмотку трансформатора тока компаундирующим сопротивлением. Это сопротивление может быть активным, индуктивным или емкостным. Помимо электрического суммирования величин, пропорциональных напряжению и току, в практике часто используется электромагнитное суммирование, для чего применяются трехобмоточные (рис.11.10, а) или трехстержневые трансформаторы (рис.11.10, б). Если на стальной сердечник насадить три катушки, две из них питать от постороннего источника тока, то выходной ток третьей катушки будет определяться величиной и фазой тока первых двух катушек. При таком суммировании также возможно амплитудно-фазовое компаундирование генератора. Принципиально суммирование трехобмоточным трансформатором не отличается от суммирования при параллельном соединении обмоток так же, как суммирование трехстержневым трансформатором – от суммирования при последовательном соединении обмоток. Действительно, в трехобмоточном трансформаторе обмотки напряжения, токовая и рабочая, замкнутая на вход выпрямителя, располагаются на одном стержне. Обе первичные обмотки можно заменить эквивалентной, мдс которой определяется геометрической суммой мдс реальных обмоток, что аналогично суммированию при параллельном соединении вторичных обмоток раздельных трансформаторов напряжения и тока.
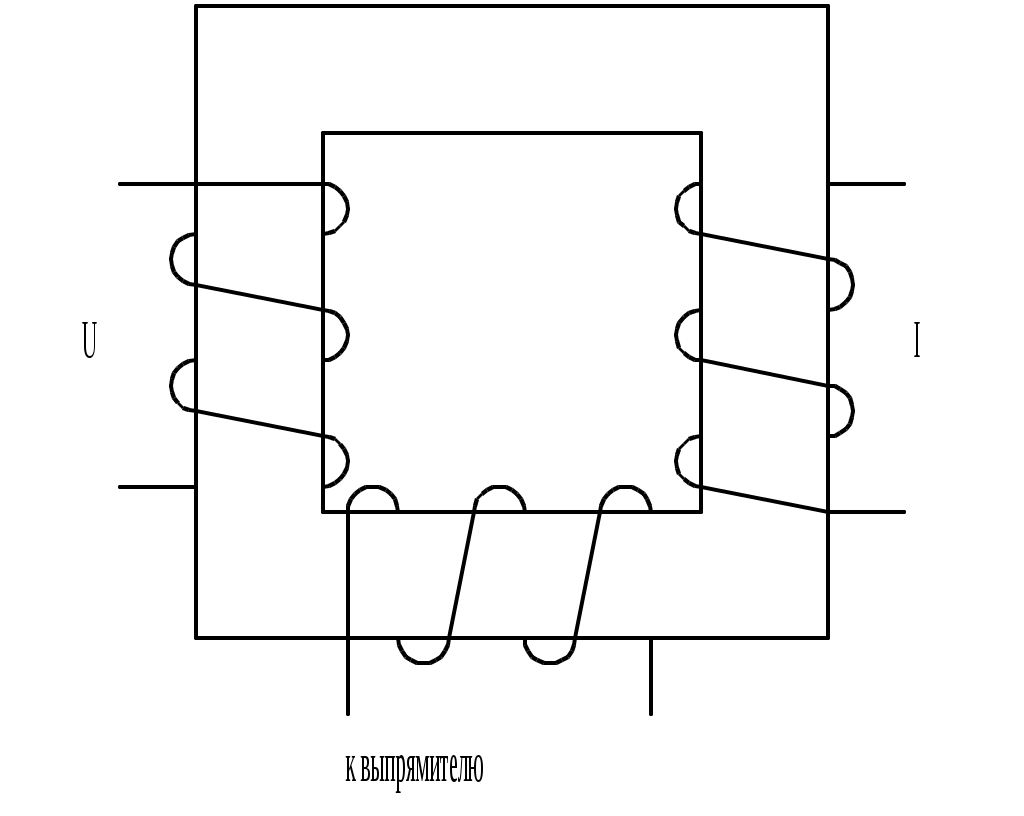
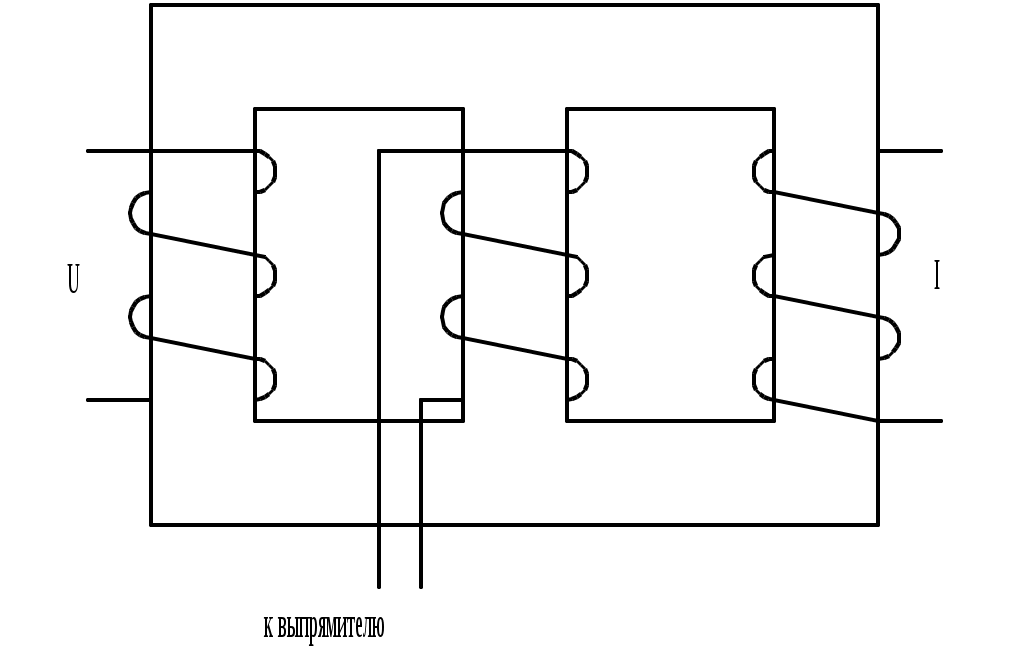
В трехстержневом трансформаторе каждая из трех обмоток располагается на одном из стержней Ш-образного магнитопровода; эдс рабочей обмотки, включенной на вход выпрямителя, определяется магнитным потоком, сцепленным с нею, равным геометрической сумме потоков в стержнях, на которых расположены первичные обмотки. Так как магнитные потоки в этих стержнях пропорциональны напряжениям, приложенным к соответствующим обмоткам, то суммирование трехстержневым трансформатором эквивалентно суммированию при последовательном соединении вторичных обмоток раздельных трансформаторов напряжения и тока. Следовательно, для нормальной работы системы в обоих случаях необходимо включать реактивные сопротивления: в первом случае – последовательно с обмоткой напряжения, во втором – параллельно токовой обмотке. В трехфазных системах нормальную работу схемы прямого амплитудно-фазового компаундирования можно обеспечить не только введением реактивных компаундирующих сопротивлений, но также и соответствующим включением обмоток трансформатора, и другими способами. На рис.11.11 изображена схема с трехобмоточным трансформатором специальной конструкции (с магнитным шунтом).
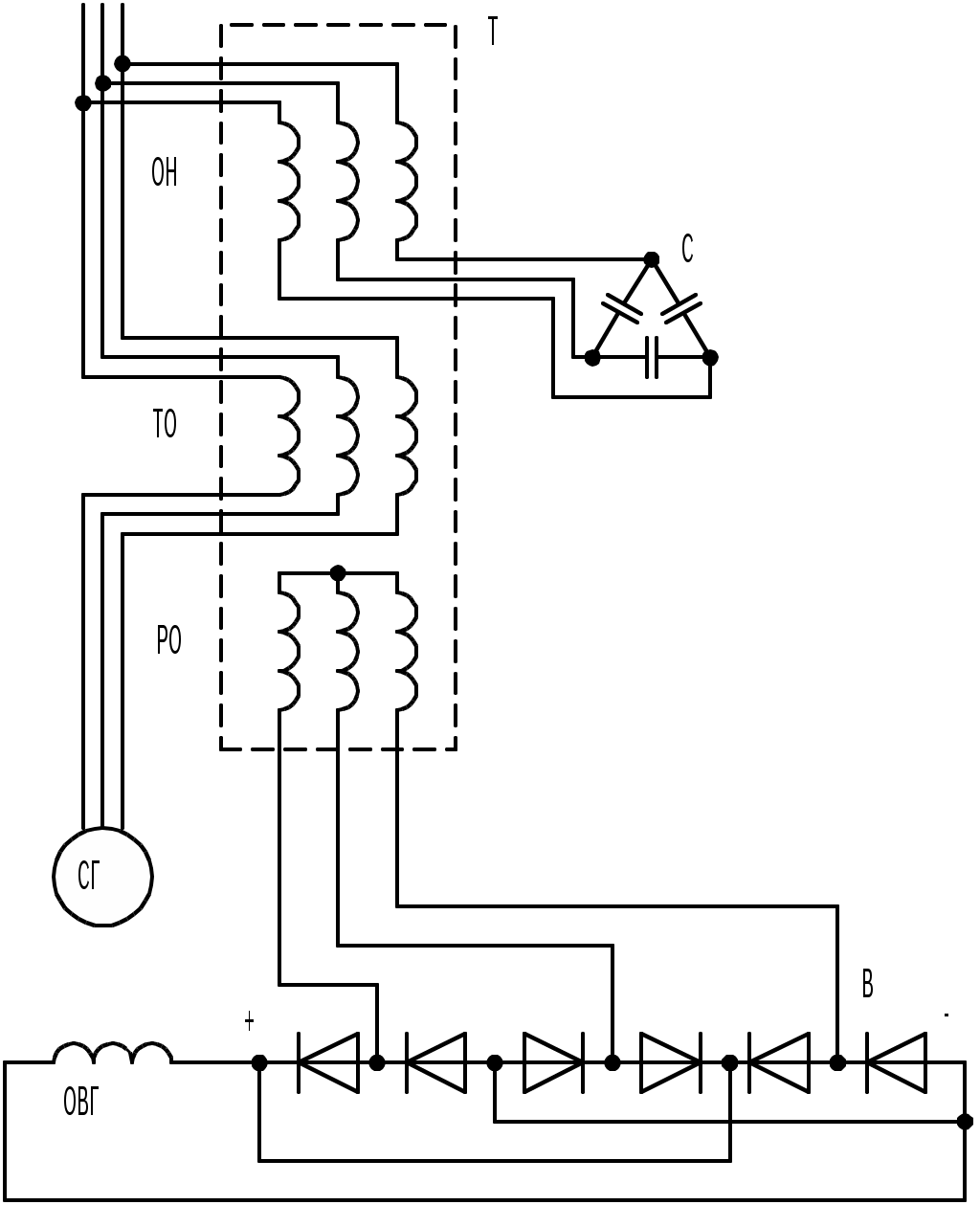
По принципу работы эта схема эквивалентна схеме с параллельным соединением вторичных обмоток трансформаторов тока и напряжения. Векторная диаграмма для этой схемы изображена на рис.11.11, а. Из нее следует, что характер суммирования составляющих тока возбуждения полностью соответствует требуемому. Магнитный шунт Ш предназначен для снижения индуктивной связи между обмотками напряжения и токовой; падение напряжения в трансформаторе благодаря этому значительно увеличивается. Роль дросселя выполняет индуктивное сопротивление рассеяния. Подобные схемы отличаются: 1. значительным быстродействием; 2. простотой устройства и надежностью в работе; 3. существенным сокращением длины генераторного агрегата за счет вобудителя и возможностью разместить отдельные элементы системы в наиболее удобных для монтажа местах. Недостаток их – трудность осуществления процесса самовозбуждения генератора. Однако эта трудность преодолевается. Например, в системе ЛЭТИ им. В.И. Ульянова (Ленина) улучшение условий самовозбуждения генератора получено благодаря соответствующему включению конденсаторов (рис.11.12).
Генератор подмагничивается током напряжения, причем ток имеет емкостный характер. Требуемый характер суммирования составляющих получен благодаря применению в канале напряжения компаундирующих элементов-конденсаторов. Заключение В данной лекции был рассмотрен принцип амлитудно-фазового компаундирования, а также основные принципы реализации систем амплитудно-фазового компаундирования СГ.
|
