Понятие о производной функции, ее геометрический и физический см. Лекция Тема
 Скачать 119.86 Kb. Скачать 119.86 Kb.
|
|
ПЛАН ЗАНЯТИЯ №2 Вид занятия лекцияТема. Понятие о производной функции, ее геометрический и физический смысл. Производная суммы, разности, произведения, частного.Цель:сформировать понятия производной функции; рассмотреть физический и геометрический смысл производной; алгоритм нахождения производной; научить вычислять производную функции, используя данный алгоритм; познакомить с правилами дифференцирования на основе определения нахождения производных некоторых элементарных функций, формировать умения применять полученные знания развить умение логически и аргументировано рассуждать, используя обобщения, анализ, сравнение; воспитывать наблюдательность в ходе отыскания математических зависимостей, повышать интерес к математике. Литература Ш.А.Алимов, Ю.М.Колянин, М.В.Ткачева, НЕ Федорова, М.И.Шабунин. Математика: алгебра и начала математического анализа 10-11 класс: учебник для общеобразовательных организаций: базовый и углубленный уровни/ Ш.А.Алимов и др./-3-е изд.-М:Просвещение, 2016. -463с. (Глава VIII, §44, 46) Мордкович А.Г. Алгебра и начала анализа. 10-11 классы.-В 2 ч. Ч.1 Учебник для учащихся общеобразовательных учреждений (базовый уровень)/ А.Г.Мордкович. – 14-е изд., стер. – М.: Мнемозина, 2013.- 400с. (Глава 5, §27, 28) Н. И. Шкиль, З. И. Слепкань, Е. С. Дубинчук .Алгебра и начала анализа :учебник для 11 класса общеобразовательных учебных заведений/Шкиль Н.И и др.;Пер. с укр.-К: Зодіак-еко, 2003 .-400с. (Глава 1 §9-10, 12) СТРУКТУРА ЗАНЯТИЯ Организационная часть Приветствие, проверка отсутствующих, задание дежурным, настрой группы на плодотворную работу. Проверка домашнего задания Актуализация опорных знаний и мотивация научной деятельности путем фронтальной беседы повторить понятие Предел функции Приращение аргумента Приращение функции Вопрос занятия Задачи, которые приводят к понятию производной Производная, ее геометрический и физический смысл Производная суммы/разности Производная произведения/частного Подведение итогов: обобщение материала Выдача задачи для самостоятельной работы студентов Лекция № 3 (занятие №3) Тема. Понятие о производной функции, ее геометрический и физический смысл. Производная суммы, разности, произведения, частного.Перейдем к основным идеям одного из важнее разделов математики – дифференциального исчисления. Методы дифференциального исчисления дают возможность свести изучение сложного процесса к более простому – равномерному, найти его скорость и ускорение, определить условия оптимального прохождения процесса, оценить допущенные погрешности, построить графики и др. Дифференциальное исчисление – раздел математики, в котором рассматривается исследования функций с помощью производных и дифференциалов. Задачи, которые приводят к понятию производной Задача 1 (о мгновенной скорости). Пусть некоторая материальная точка движется по оси x, так что x(t) есть координата точки в момент времени t. Спустя время 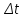 координата точки будет координата точки будет 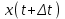 , т.е. за время , т.е. за время 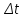 точка пройдет путь точка пройдет путь 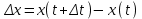 . Поэтому средняя скорость точки за интервал времени . Поэтому средняя скорость точки за интервал времени 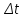 будет равна будет равна 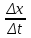 . Чтобы найти мгновенную скорость точки в момент времени . Чтобы найти мгновенную скорость точки в момент времени 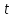 надо устремить надо устремить 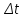 к нулю, то есть к нулю, то есть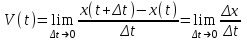 Задача 2 (о касательной к графику). Пусть кривая задана уравнением 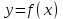 . Соединим две ее точки М0( . Соединим две ее точки М0(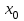 , , 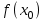 ) и М( ) и М(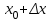 , , 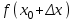 ) секущей. ) секущей.Тогда дробь 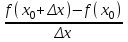 = = 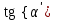 , где , где 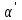 есть угол наклона секущей к оси OX (в треугольнике М0МТ отношение катетов) есть угол наклона секущей к оси OX (в треугольнике М0МТ отношение катетов) При 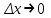 точка M начинает двигаться к точке M0. При этом вся секущая будет поворачиваться около точки M0 и в пределе она превратиться в касательную к точке M0. Угол точка M начинает двигаться к точке M0. При этом вся секущая будет поворачиваться около точки M0 и в пределе она превратиться в касательную к точке M0. Угол 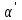 при этом перейдет в угол при этом перейдет в угол 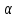 , который эта касательная образует с осью х. Поэтому можно утверждать, что , который эта касательная образует с осью х. Поэтому можно утверждать, что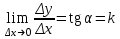 , ,где 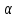 угол, образованный касательной к кривой в точке угол, образованный касательной к кривой в точке 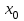 и осью OX, k угловой коэффициент касательной. и осью OX, k угловой коэффициент касательной.Задача 3 (о скорости химической реакции) Пусть (t) есть количество вещества прореагировавшего за время t. Спустя время 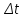 количество прореагировавшего вещества будет количество прореагировавшего вещества будет 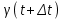 , т.е. за время , т.е. за время 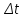 количество прореагировавшего вещества количество прореагировавшего вещества 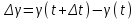 . Поэтому средняя скорость химической реакции за интервал времени . Поэтому средняя скорость химической реакции за интервал времени 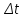 будет равна будет равна 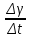 . Чтобы найти мгновенную скорость химической реакции в момент времени . Чтобы найти мгновенную скорость химической реакции в момент времени 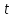 надо устремить надо устремить 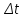 к нулю, то есть к нулю, то есть 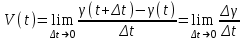 Поскольку с помощью предела 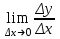 решают кроме рассмотренных ещё и много других важнейших задач (например: задача о величине переменного тока, который течет в проводнике; нахождении линейной плотности неоднородного стержня, теплоемкости тела при его нагревании, угловой скорости тела, которое вращается и многие др), то целесообразно всесторонне изучить данный предел, в частности, указать способы его вычисления. Этот предел в математике и носит название производной. решают кроме рассмотренных ещё и много других важнейших задач (например: задача о величине переменного тока, который течет в проводнике; нахождении линейной плотности неоднородного стержня, теплоемкости тела при его нагревании, угловой скорости тела, которое вращается и многие др), то целесообразно всесторонне изучить данный предел, в частности, указать способы его вычисления. Этот предел в математике и носит название производной.Производная, ее геометрический и физический смысл Определение: Производной данной функции y=f(x) называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее стремится к нулю и такой предел существует и конечен. Заметим, что производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x) Производная обозначается символами f'(x), y', Операция нахождения производной от функции f(x) называется дифференцированием этой функции. Для непосредственного нахождения производной по определению можно применить следующее практическое правило: Придать x приращение Δx и найти наращенное значение функции f(x + Δx). Найти приращение функции Δy = f(x + Δx) – f(x). Составить отношение 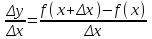 и найти предел этого отношения при Δx→0. и найти предел этого отношения при Δx→0. Примеры. Найти производную функции y = x2 а) в произвольной точке; б) в точке x= 2. а) f(x + Δx) = (x + Δx)2; Δy = (x + Δx)2 – x2=2xΔx– x2; б) f '(2) = 4 Используя определение найти производную функции Учитывая задачи о мгновенной скорости и касательной к графику легко построить следующие утверждения: Физический смысл производной: скорость неравномерного движения это производная от пройденного пути по времени. 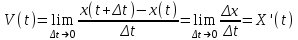 Геометрический смысл производной: у'(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0 (т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М0(x;y) с положительным направлением оси Ox). Определение. Касательной к графику функции в точке М0(x0, y0) назовем предельное положение секущей М0М, когда точка М, двигаясь вдоль кривой, стремиться к совпадению с точкой М0.. Уравнение касательной к графику функции в точке М0 (x0, y0): 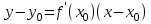 . .(вывод формулы самостоятельно, у=kx+b-уравнение прямой, k= 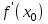 ) )Производная суммы/разности Итак, мы дали определение производной, объяснили ее физический и геометрический смысл. Теперь необходимо сделать следующий шаг - рассмотреть правила дифференцирования. Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x. Основные правила дифференцирования выражаются формулами: 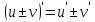 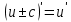 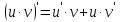 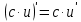 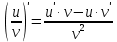 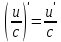 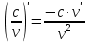 Формулы 1 и 2 докажите самостоятельно. Доказательство формулы 1. Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx). Тогда Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv. Следовательно, (построить вывод следствия) Производная произведения/частного Доказательство формулы 2. Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x). Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0. Поэтому можем записать 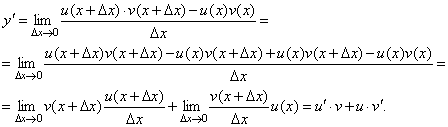 На основании этого свойства можно получить правило дифференцирования произведения любого числа функций. Пусть, например, y=u·v·w. Тогда, y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '. (построить вывод следствия) Доказательство формулы 3. Пусть 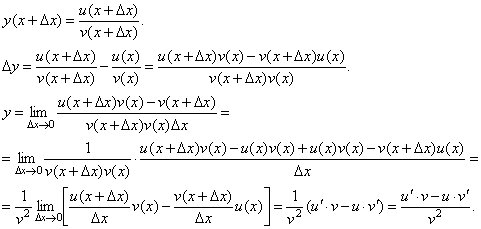 При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0. (построить вывод следствий) Вопросы для самопроверки 1) При каком движении средняя скорость всегда совпадает с мгновенной? 2) Закон прямолинейного движения тела выражается формулой x = kt + b. Какое механическое содержание коэффициентов k, b? 3) Дать определения производной заданной функции. 4) Охарактеризовать символы 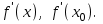 5) Который геометрический и физический смысл производной? 6) Как найти производную, исходя из ее определения? 7) Доказать, пользуясь определением производной, 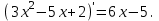 Задания для самостоятельного решения [ш -11]– прочитать § 6,7,8, ответить на вопросы стр.49; выполнить задания №17,18(1,2). Исходя из определения производной, непосредственно найти производные от функций в заданных точках: а) 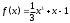 вычислить вычислить 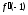 и и 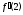 . . 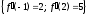 . .б) 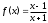 вычислить вычислить 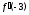 и и 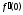 . . 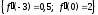 . . |
