Лекция 5. Лекция Туынды. Туындыны геометриялы жне физикалы маыналары. Функцияны нктедегі дифференциалдануы. Функцияны дифференциалдануы мен зіліссіздігі арасындаы байланыс. Дифференциалдау ережелері. Элементар функцияларды дифференциалдау
 Скачать 143.97 Kb. Скачать 143.97 Kb.
|
|
Лекция 4. Туынды. Туындының геометриялық және физикалық мағыналары. Функцияның нүктедегі дифференциалдануы. Функцияның дифференциалдануы мен үзіліссіздігі арасындағы байланыс. Дифференциалдау ережелері. Элементар функцияларды дифференциалдау. 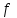 функциясы функциясы 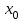 нүктесінде және оның қандайда бір маңайында анықталған функция болсын. нүктесінде және оның қандайда бір маңайында анықталған функция болсын. 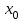 - нүктесіндегі аргумент өсімшесі - нүктесіндегі аргумент өсімшесі 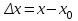 , ал оған сәйкес келетін функция өсімшесі: , ал оған сәйкес келетін функция өсімшесі: 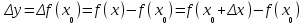 арқылы белгіленсін. Анықтама. Егер 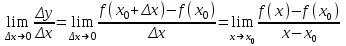 нақты мәнді шегі бар болса, онда шектің мәнін нақты мәнді шегі бар болса, онда шектің мәнін 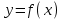 функциясының функциясының 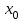 - нүктесіндегі туындысы дейді де - нүктесіндегі туындысы дейді де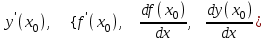 символдарының бірімен белгіленеді. Сонымен, 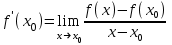 (1) (1)немесе 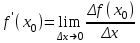 Егер (1) - шек 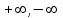 немесе немесе 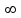 болса, онда болса, онда 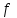 функциясының функциясының 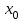 - нүктесінде ақырсыз туындысы бар дейді. - нүктесінде ақырсыз туындысы бар дейді.Егер (1) - теңдіктегі шек 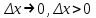 немесе немесе 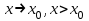 жағдайында қарастырылса, онда шек (егер ол бар болса) жағдайында қарастырылса, онда шек (егер ол бар болса) 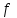 функциясының функциясының 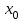 нүктесіндегі оң жақты туындысы, ал нүктесіндегі оң жақты туындысы, ал 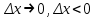 немесе немесе 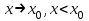 жағдайында қарастырылса, онда сол жақты туындысы деп аталады да, олар сәйкес жағдайында қарастырылса, онда сол жақты туындысы деп аталады да, олар сәйкес 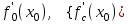 символдары арқылы белгіленеді. символдары арқылы белгіленеді.Функцияның 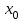 нүктесінде туындысы бар болуы үшін: нүктесінде туындысы бар болуы үшін:1) 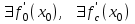 ; 2) ; 2) 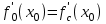 шарттарының орындалуы қажетті және жеткілікті. Онда шарттарының орындалуы қажетті және жеткілікті. Онда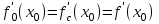 . (2) . (2)Теорема. Егер 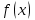 функциясының функциясының 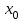 нүктесінде ақырлы туындысы бар болса, онда нүктесінде ақырлы туындысы бар болса, онда 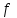 функциясы осы функциясы осы 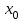 - нүктесінде үзіліссіз болады. - нүктесінде үзіліссіз болады.Ескерту. Функция нүктеде үзіліссіз болса да, оның бір жақты ақырлы туындылары болмауы да мүмкін. Мысал ретінде мынадай функцияны қарастырайық: 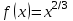 , , 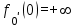 , , 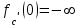 Сонымен, функция нүктеде үзіліссіз болғанымен, ол нүктеде функцияның туындысы болмауы мүмкін екен. Салдар. Егер 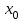 нүктесі нүктесі 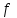 функциясының үзіліс нүктесі болса, онда осы нүктеде функциясының үзіліс нүктесі болса, онда осы нүктеде 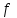 - тің ақырлы туындысы болмайды. - тің ақырлы туындысы болмайды.Туындының механикалық және геометриялық мағынасы Лездік жылдамдық. 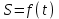 материялық нүктенің түзудегі қозғалысының заңдылығын өрнектейтін функция болсын. материялық нүктенің түзудегі қозғалысының заңдылығын өрнектейтін функция болсын. 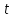 уақытқа дейін материялық нүкте уақытқа дейін материялық нүкте 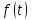 , ал , ал 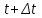 уақытқа дейін уақытқа дейін 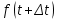 жол жүреді. Сондықтан жол жүреді. Сондықтан 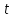 -ден -ден 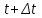 уақытқа дейін ол уақытқа дейін ол 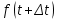 - -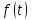 жол жүреді. Бұл жолды қозғалыс уақыты жол жүреді. Бұл жолды қозғалыс уақыты 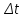 -ға бөліп, қозғалыстың -ға бөліп, қозғалыстың 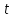 -ден -ден 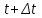 -ға дейінгі уақыт аралығындағы орташа жылдамдығын табамыз: -ға дейінгі уақыт аралығындағы орташа жылдамдығын табамыз: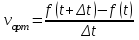 . .Бұл жылдамдықтың 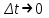 жағдайдағы шегі (егер бар болса) қозғалыстың жағдайдағы шегі (егер бар болса) қозғалыстың 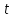 уақыт кезеңіндегі лездік жылдамдығы деп аталады: уақыт кезеңіндегі лездік жылдамдығы деп аталады: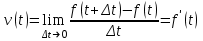 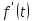 туынды материялық нүктенің туынды материялық нүктенің 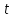 мезгіліндегі жылдамдығы болады. мезгіліндегі жылдамдығы болады.Жанама туралы есеп. 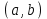 аралығында үзіліссіз аралығында үзіліссіз 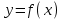 функциясы берілсін. Оның функциясы берілсін. Оның 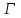 - графигінен - графигінен 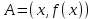 нүктесін белгілеп (1-2 суреттер) осы нүктедегі қисыққа жүргізілген жанаманы анықтайық. Ол үшін нүктесін белгілеп (1-2 суреттер) осы нүктедегі қисыққа жүргізілген жанаманы анықтайық. Ол үшін 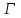 - қисығынан басқа - қисығынан басқа 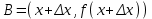 нүктесін аламыз (1 - суретте нүктесін аламыз (1 - суретте 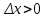 , ал 2 - суретте , ал 2 - суретте 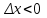 жағдайы көрсетілген). жағдайы көрсетілген). 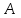 мен мен 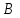 нүктелері арқылы өтетін, нүктелері арқылы өтетін, 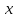 - тің өсу жағына қарай бағытталған - тің өсу жағына қарай бағытталған 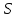 түзуін қиюшы деп атаймыз. Оның түзуін қиюшы деп атаймыз. Оның 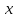 - өсінің оң бағытымен арасындағы бұрышын - өсінің оң бағытымен арасындағы бұрышын 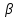 деп белгілейік және деп белгілейік және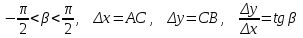 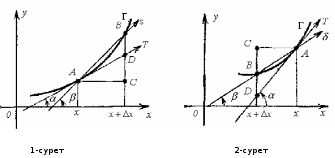 . Егер  , онда , онда  және В нүктесі және В нүктесі 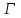 қисығы бойымен қисығы бойымен 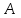 - нүктесіне ұмтылады. Осыдан - нүктесіне ұмтылады. Осыдан 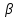 бұрышы қандайда бір бұрышы қандайда бір 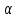 мәніне мәніне 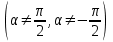 ұмтылса, онда ұмтылса, онда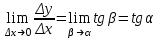 шегі бар және ол 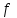 функциясының функциясының 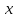 нүктесіндегі туындысына тең: нүктесіндегі туындысына тең: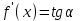 . . Керісінше, егер 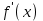 туындысы бар болса, онда туындысы бар болса, онда 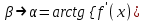 . .Анықтама.  - қисығының - қисығының 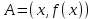 нүктесіндегі жанамасы деп нүктесіндегі жанамасы деп 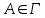 және және 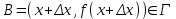 нүктелері арқылы өтетін ( нүктелері арқылы өтетін (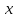 - тің өсу жағына қарай бағытталған) - тің өсу жағына қарай бағытталған) 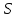 - қиюшының - қиюшының 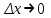 ұмтылатын ұмтылатын 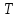 - түзуін айтады. - түзуін айтады. Аналитикалық геометриядан 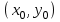 нүктесі арқылы өтетін бұрыштық коэффициенті нүктесі арқылы өтетін бұрыштық коэффициенті 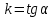 , , 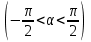 болатын түзу теңдеуі болатын түзу теңдеуі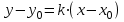 түрінде жазылатыны белгілі. Олай болса,  қисығының қисығының 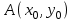 нүктесіндегі жанама теңдеуі нүктесіндегі жанама теңдеуі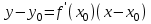 (3) (3)түрінде, ал 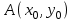 нүктедегі нормаль теңдеуі. нүктедегі нормаль теңдеуі.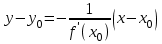 (4) (4)түрінде жазылады. |
