Лекция№3
Разработка нефтяных месторождений при упругом режиме.
Первая книга о режимах разработки пластов появилась в США под названием «Аналитические основы добычи нефти и воды из скважин». Ее автор – Стенли Геронд. На русском языке она была издана в 1932 г.
Идея существования упругого режима разработки нефтяных пластов была высказана проф. И.Н.Стрижовым еще в 1920-х годах. В дальнейшем она была развита (в частности М. Маскетом) рядом зарубежных и отечественных исследователей. В настоящее время теория упругого режима разработки нефтяных залежей разработана достаточно трудами таких ученых как М. Маскет, Д. Шилсюиз, У. Херст, В.Н. Щелкачев, А.Т. Горбунов и др.
Основным признаком упругого режима является однофазность фильтрационного потока, т.е. условие превышения пластового давления над давлением насыщения.
Если упругие деформации считать квазилинейными и подчиняющимися закону Гука, полученному для однородного пласта, то можно записать:
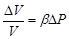 (1) (1)
или в дифференциальной форме
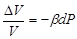 (2) (2)
где V – объем упругого тела; Р – давление; β – коэффициент объемной упругости тела (сжимаемость).
Объемная упругость нефти зависит от давления, температуры, ее фракционного состава и количества растворенного газа. Для условий месторождений России она изменяется в достаточно широких пределах – от 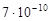 до до 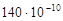 1/Па. 1/Па.
Сжимаемость пластовых вод изменяется в небольших пределах от 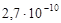 до до 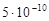 1/Па. 1/Па.
При наличии растворенного газа в минерализованной воде ее сжимаемость будет равна:
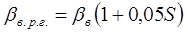 (3) (3)
где βв - упругость воды без растворенного газа, 1/Па;
S – количество растворенного газа, м3/м3.
Сжимаемость горных пород зависит от условий залегания продуктивных пластов, величины горного давления и характера изменения напряженного состояния пород при разработке залежи. В диапазоне внешнего давления от 0 до 100 МПа величина сжимаемости горных пород изменяется в пределах от 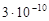 до до 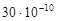 1/Па. 1/Па.
Упругий запас залежи.
Под упругим запасом залежи понимается количество нефти (флюида), которое может быть извлечено за счет упругих сил пласта и пластовых флюидов. Упругий запас определяется расширением нефти, воды и породы при снижении давления. Аналитически, согласно закону Гука, можно записать:
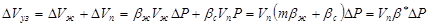 (4) (4)
где 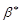 - коэффициент упругоемкости пласта, 1/Па; Vп – геометрический объем пласта, м3; - коэффициент упругоемкости пласта, 1/Па; Vп – геометрический объем пласта, м3; 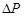 - понижение пластового давления - понижение пластового давления 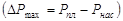 . .
Чтобы оценить численно возможности упругого режима рассмотрим следующий пример. Обозначения общепризнанные.
Исходные данные.
Vп = 109 м3; m = 0,2; βж = 10-9 1/Па; βс = 10-91/Па; Sн = 1,0; 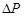 =10 МПа. =10 МПа.
Коэффициент упругоемкости пласта равен 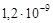 1/Па, упругий запас - 1/Па, упругий запас - 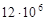 м3, начальный геологический запас нефти в продуктивном пласте - м3, начальный геологический запас нефти в продуктивном пласте - 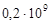 м3. м3.
Тогда нефтеотдача пласта при упругом режиме для принятых условий составляет 0,06 или 6%.
Видно, что возможности упругого режима весьма незначительные. Упругий режим – это естественный режим истощения залежи.
Гидродинамическая теория упругого режима впервые была разработана М. Маскетом, Д Шилсюизом и У Херстом в 1937 г. На начальном этапе создания теории упругого режима в работах М. Маскета и Т. Мура и других при определении упругоемкости пласта сжимаемостью породы пренебрегали и полагали, что
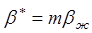 (5) (5)
Наиболее полно теория упругого режима дана профессором В.Н. Щелкачевым.
Необходимость учета сжимаемости породы была им показана на основании результатов экспериментальных исследований Д.А. Антонова (1952 г.). К аналогичному выводу пришел и американский ученый Х.Холл в 1953 г.
Упругие деформации могут быть обратимыми и необратимыми. Экспериментально это было подтверждено исследованиями В.М. Добрынина. Теоретическое описание было сделано Г.И. Баренблаттом и А.П. Крыловым и названо упруго-пластическим режимом (по определению проф. И.Н. Стрижова – упруго-грузовой режим). Дальнейшее развитие теории механизма этого процесса было дано В.Н.Николаевским и А. Т. Горбуновым.
Изменение давления при упругом законе упругости описывается дифференциальным уравнением пьезопроводности по аналогии с известным уравнением теплопорводности Фурье, известным в математической физике с начала XIX века.
Уравнение пьезопроводноси имеет вид:
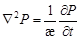 (6) (6)
где æ – коэффициент пьезопроводности горной породы, характеризует распределения давления в пласте, предложен проф. В.Н. Щелкачевым по аналогии с коэффициентом температуропроводности в уравнении Фурье. Решение уравнения теплопроводности впервые получено Лапласом.
Для плоско-радиальной фильтрации уравнение пьезопроводности имеет вид:
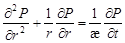 (7) (7)
с учетом инерционных сил:
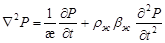 (8) (8)
и в случае неизотермической фильтрации:
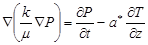 (9) (9)
где 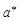 - коэффициент, учитывающий объемное расширение жидкости и среды. - коэффициент, учитывающий объемное расширение жидкости и среды.
Такое решение уравнения пьезопроводности при определенных начальных и граничных условиях было получено Ван-Эвердингеном и У. Херстом виде интегрального выражения, куда входят функции Бесселя.
Если обозначить нижеприведенное соотношение 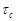 - безразмерное время: - безразмерное время:
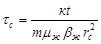 (10) (10)
то при 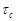 >100 решение можно представить в виде: >100 решение можно представить в виде:
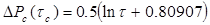 (11) (11)
Разновидности упругого режима.
e Упруго-замкнутый режим, который проявляется в замкнутых (изолированных от законтурной области) пластах;
e Упруговодонапорный, который имеет место в залежах со значительной по размерам законтурной водоносной областью.
При разработке нефтяных месторождений на упругом режиме выделяют две фазы:
e первая фаза;
e вторая фаза.
Первая фаза существует до тех пор, пока возмущение от пуска скважины в работу, не достигнет контура нефтеносности (т.е. когда 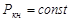 ). При этом её длительность равна: ). При этом её длительность равна:
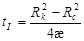 (12) (12)
Положение границы области пониженного давления оценивают по формуле Э.Б. Чекалюка:
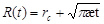 (13) (13)
Вторая фаза наступает с момента изменения давления на контуре нефтеносности.
Теория упругого режима создавалась трудами многих ученых как отечественных, так и иностранных. В их числе:
Отечественные ученные
|
Иностранные ученные
|
И.Н.Стрижов
|
Т.Мур
|
А.П.Крылов
|
Р.Шилсюиз
|
В.Н.Щелкачев
|
У.Херст
|
И.А.Чарный
|
М.Маскет
|
Б.Б.Лапук
|
Ван-Эвердинген
|
Г.И.Баренблатт
|
|
Г.П.Гуссейнов
|
|
Э.Б.Чекалюк
|
|
К.А.Царевич
|
|
А.А.Пирвердян
|
|
В.Н.Николаевский
|
|
Ю.П.Желтов
|
|
А.Т.Горбунов
|
|
Замкнуто-упругий режим. Этот режим существует в замкнутых (изолированных) залежах с ограниченной законтурной водоносной областью.
Рассмотрим первую фазу упругого режима при пуске скважины с постоянным дебитом.
Первая фаза упругого режима.
Распределение давления в приведенной области влияния скважины можно определить с использованием многих формул:
v Дюпюи
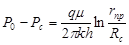 , (14) , (14)
где: - по И.А.Чарному 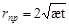 ; ;
- по Э.Б. Чекалюку 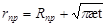 . .
v А.М.Пирвердяна
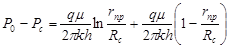 , (15) , (15)
где: 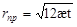
v Г.П.Гусейнова
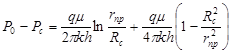 , (16) , (16)
где 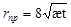 . .
v По упрощенной основной формуле упругого режима
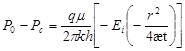 (17) (17)
Сопоставление результатов расчетов по указанным формулам, сделанные В.Н.Щелкачевым показало, что наилучшие результаты дает упрощенная основная формула упругого режима, которая справедлива для бесконечного пласта.
Вторая фаза упругого режима. Изменение давления на стенке скважины и на конкуре нефтеносности (или непроницаемой границе) во второй фазе упругого режима можно определить по формулам:
v И.А.Черного
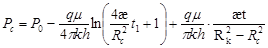 (18) (18)
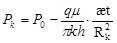 , ,
где t1 – продолжительность 1й фазы.
v Г.И.Баренблатта
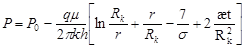 (19) (19)
при 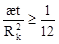 ; ;
v Строгой гидродинамической формуле (при Rк>>Rс) (Решение уравнения пьезопроводности при соответствующих начальных и граничных условиях)
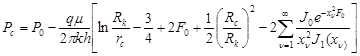 (20) (20)
при 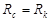 получаем получаем
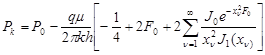 , ,
где 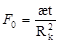 - параметр Фурье. - параметр Фурье.
J0,J1 – символы функций Бесселя первого рода соответственно нулевого и первого порядков.
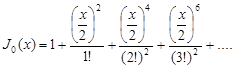
q – установившийся дебит скважины.
Согласно исследованиям В.Н.Щелкачева, более точной считается гидродинамическая формула.
Для 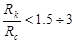 следует пользоваться режимом Ван-Эвердингена и У.Херст и А.Хупера. следует пользоваться режимом Ван-Эвердингена и У.Херст и А.Хупера.
Понятие об укрупненной скважине.
При проведении расчетов для месторождения в целом пользуются понятием укрупненной скважины. Радиус такой скважины равен:
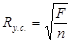 , ,
где F – площадь месторождения.
В расчетах для укрупненной скважины, когда 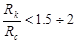 пользоваться строгой гидродинамической формулой нельзя и следует использовать формулы М.Маскета, А.Хупера, А. Ван-Эвердингена, У.Херста. Так, формула М.Маскета, имеет вид: пользоваться строгой гидродинамической формулой нельзя и следует использовать формулы М.Маскета, А.Хупера, А. Ван-Эвердингена, У.Херста. Так, формула М.Маскета, имеет вид:
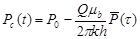 (21) (21)
где: 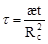
Функция 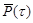 подсчитана А. Ван-Эвердингеном и У.Херстом для значений подсчитана А. Ван-Эвердингеном и У.Херстом для значений 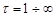
Круговая залежь ограниченном пласте.
А) первая фаза
Для расчетов 1й фазы упругого режима предпочтительнее пользоваться формулами:
v Э.Б.Чекалюка
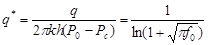 , (22) , (22)
где q* и q соответственно безразмерный и размерный дебит скважины;
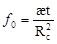 - параметр Фурье. - параметр Фурье.
v Б.А.Богачева
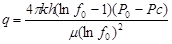 (23) (23)
погрешность этой формулы не превышает 1,2%
б) вторая фаза
Рекомендуется пользоваться формулой В.Н.Щелкачева (При Rk>>Rc с точностью до 3-8%)
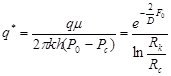 , (24) , (24)
где 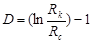
Упруговодонапорный режим.
Это наиболее распространенный режим в практике РНМ. Он может быть как искусственным, так и естественным.
Доля естественного УВНР составляет в годовой добыче России около 6%, а искусственного – более 90% всей добываемой нефти извлекается из терригенных коллекторов, а остальное количество – из карбонатов. Искусственный УВНР на 98% обеспечивается внутриконтурным заводнением, в том числе 10% за счет площадного и избирательного.
Подавляющее большинство объектов (70%) разрабатывается при плотности сетки скважин от 10 до 50 га/скв. На долю этих объектов приходиться около 90% добываемой за счет заводнения нефти.
Наиболее распространенные сетки скважин 20-30 га/скв.
Рассмотрим особенности естественного УВНР.
Круговая залежь в неограниченном пласте.
Пуск скважины с постоянным дебитом.
Перераспределение давления в пласте после пуска возмущающей скважины можно рассчитать с помощью формулы, которая давно известна в математической физике, но для подземной гидродинамики впервые применена Тсейсом.
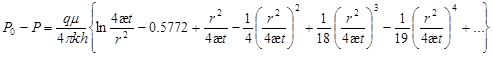 , (25) , (25)
где r – расстояние от скважины до точки, где давление равно Р,
q – установившийся дебит скважины.
Используя понятие об упрощенной интегральной экспоненциальной функции –Ei(-x), получим:
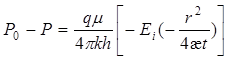 , (26) , (26)
где 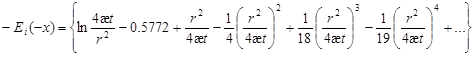
Точное решение, для укрупненной скважины, уравнения пьезопроводности в общем виде, в случае развития У.Р. в законтурной области и поступление воды в нефтяную зону, было получено А. Ван-Эвердингеном и У.Херетом в виде:
(из уравнения пьезопроводности при q=const, P=P0 при t=0, 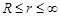 ) )
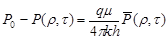 , (27) , (27)
где
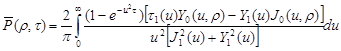 (28) (28)
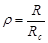 ; ;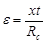 ; ;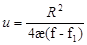 - пространство измерения. - пространство измерения.
J0(u,r);J1(u);Y0(u,r);Y1(u) – функции Бесселя нулевого и первого рода, нулевого и первого порядка от мнимого аргумента.
Для r=1¸¥ функция 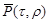 табулирована. табулирована.
Для r=1 можно воспользоваться аппроксимацией Ю.Л.Желтова.
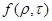 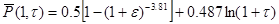 (29) (29)
Имеются также решения М. Маскета, В.Н.Щелкачева, Г.И. Баренблатта,А.М. Пирвердяна, И.А.Чарного, М.А. Гусейн-заде и А.К. Колосовской и др.
Пуск скважины с постоянным забойным давлением.
Дебит и накопленную добычу можно определить по формулам М. Маскета (для галереи):
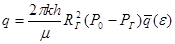 (30) (30)
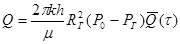 (31) (31)
где Rг – радиус галереи
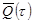 и и 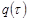 - безразмерные функции дебита и накопленной добычи (табулированы У. Херстом, А. Ван-Эвердингеном). - безразмерные функции дебита и накопленной добычи (табулированы У. Херстом, А. Ван-Эвердингеном).
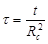 æ. æ.
Учет различия гидропроводностей нефтяной и законтурной областей.
По предложению А.П. Крылова для расчетов при УВНР пользуются поправочным коэффициентом:
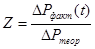 , (32) , (32)
В.С. Орловым предложено учитывать два коэффициента z1 – учитывающий различие гидропроводностей и z2 – учитывающий различие пьезопроводностей нефтяной и водяной частей залежи.
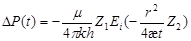 . . |
 Скачать 121.72 Kb.
Скачать 121.72 Kb.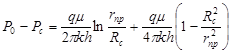 , (16)
, (16)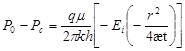 (17)
(17)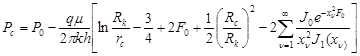 (20)
(20)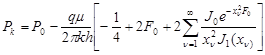 ,
,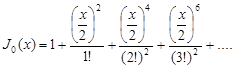
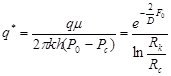 , (24)
, (24)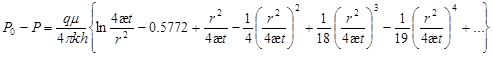 , (25)
, (25)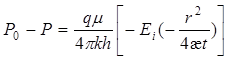 , (26)
, (26)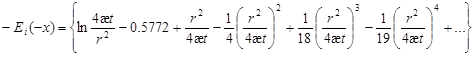
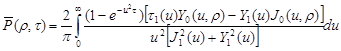 (28)
(28)