3 динамика материальной точки. Лекторсоставитель д п. н. Базарова С. Дж
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
республика узбекистан навоийский горно-металлургический комбинат Энерго-механический факультет Кафедра «Общая физика»Предмет «Физика» на тему:  Лектор-составитель: д.п.н. Базарова С.Дж Навои - 2018 Базарова С.Дж. Разработка «открытой лекции» на тему «Динамика материально точки». –Н.: НГГИ, 2018. Настоящая разработка спроектирована c учетом правил технологизации обучения: дидактических принципов, способов и регуляторов разработки технологий лекционных занятий, их существенных признаков на основе учебно-методических материалов, отражающие основы технологизации данной формы обучения в техническом вузе. В разработке представлены информативные материалы по эффективной организации лекционного, раскрывающие теоретические основы, принципы и структуру изучаемой темы, условия эффективности преподавания с интерактивной методикой преподавания на основе составленными автором-лектором модели технологизации обучения и технологической карты учебного занятия. Предназначено для студентов 1 курса направления образования «Горное дело», «Электроэнергетика», «Металлургия» и молодых преподавателей-педагогов технических вузов и других направлений профессиональной подготовки, Модель технологии обучения на учебном занятии Тема «Динамика материальной точки». Технология обучения на __«открытом лекционном занятии»__
Технологическая карта учебного занятия
  3.1. Первый закон Ньютона. Инерциальные системы 3.2. Масса и импульс тела 3.3. Второй закон Ньютона. Принцип суперпозиции 3.4. Третий закон Ньютона 3.5. Импульс произвольной системы тел 3.6. Основное уравнение динамики поступательного движения произвольной системы тел 3.7. Закон сохранения импульса Литература и источники: Г.А.Зисман, О.М.Тодас «Курс физики. 2 часть» К.И. Трофимова «Курс физики» Б.М.Яворский, А.А. Детлаф «Курс физики. 2 часть» И.В.Савельев «Курс общей физики» К.А Путилов «Курс физики. 2 часть» С.А. Фриш «Курс физики» Интернет-сайты: www.gov.uz, www.ziyonet.uz, www.ref.uz, www.referat.ruи др. 3.1. Первый закон Ньютона. Инерциальные системыВ основе так называемой классической, или ньютоновской, механики лежат три закона динамики, сформулированных И. Ньютоном в 1687 г. Эти законы играют исключительную роль в механике и являются (как и все физические законы) обобщением результатов огромного человеческого опыта. Законы Ньютона рассматривают как систему взаимосвязанных законов и опытной проверке подвергают не каждый отдельный закон, а всю систему в целом. Ньютоновская механика оказалась настолько плодотворной, настолько могущественной, что у физиков сложилось представление о том, что любое физическое явление можно объяснить с помощью ньютоновских законов. Большинство физиков к концу XIX в. были убеждены в том, что они уже знают о природе всё, что можно было узнать. Однако наиболее проницательные физики понимали, что в знании классической физики есть слабые места. Так, например, английский физик У. Томсон (он же лорд Кельвин) говорил, что на горизонте безоблачного неба классической физики имеются два тёмных облачка: неудача попыток создания теории абсолютно чёрного тела и противоречивое поведение эфира – гипотетической среды, в которой предполагалось распространение световых волн. Эти факты получили своё объяснение в новых теориях – специальной теории относительности и квантовой механике. В специальной теории относительности, созданной А. Эйнштейном в 1905 г., подверглись радикальному пересмотру ньютоновские представления о пространстве и времени. Этот пересмотр привёл к созданию «механики больших скоростей», или, как её называют, релятивистской механики. Новая механика не привела, однако, к полному отрицанию старой ньютоновской механики. Уравнения релятивистской механики, в пределе (для скоростей малых, по сравнению со скоростью света), переходят в уравнения классической механики. Таким образом, классическая механика вошла в релятивистскую механику как её частный случай и сохранила своё прежнее значение для описания движений, происходящих со скоростями значительно меньшими, чем скорость света. Аналогично обстоит дело и с соотношениями в классической и квантовой механике, возникшей в 20-х годах прошлого века в результате развития физики атома. Уравнения квантовой механики также дают в пределе (для масс больших, по сравнению с массами атомов) уравнения классической механики. Следовательно, классическая механика вошла в квантовую механику в качестве её предельного случая. Таким образом, развитие науки не перечеркнуло классическую механику, а лишь показало её ограниченную применимость. Классическая механика, основывающаяся на законах Ньютона, является механикой тел больших (по сравнению с массой атомов) масс, движущихся с малыми (по сравнению со скоростью света) скоростями. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её (его) изменить это состояние. Оба названных состояния схожи тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остаётся постоянной (в частности, равной нулю), пока воздействие на это тело со стороны других тел не вызовет её изменения. Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют законом инерции. Механическое движение относительно, и его характер зависит от системы отсчёта. Первый закон Ньютона выполняется не во всякой системе отсчёта, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчёта. Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью). Таким образом, первый закон Ньютона утверждает существование инерциальных систем отсчёта. Опытным путём установлено, что инерциальной системой отсчёта можно считать гелиоцентрическую (звёздную) систему отсчёта (начало координат находится в центре Солнца, а оси проведены в направлении определённых звёзд). Система отсчёта, связанная с Землей, строго говоря, неинерциальная, однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач малы, и в этих случаях её можно считать инерциальной. Из приведённых выше примеров легко понять, что основным признаком инерциальной системы является отсутствие ускорения. Сущность первого закона Ньютона может быть сведена к трём основным положениям: все тела обладают свойствами инерции; существуют инерциальные системы отсчёта, в которых выполняется первый закон Ньютона; движение относительно. Если тело А движется относительно тела отсчета В со скоростью υ, то и тело В, в свою очередь, движется относительно тела А с той же скоростью, но в обратном направлении 3.2. Масса и импульс телаВоздействие на данное тело со стороны других тел вызывает изменение его скорости, т.е. сообщает данному телу ускорение. Опыт показывает, что одинаковое воздействие сообщает различным телам разные по величине ускорения. Всякое тело противится попыткам изменить его состояние движения. Это свойство тел, как мы уже говорили, называется инертностью (следует из первого закона Ньютона). Мерой инертности тела является величина, называемая массой. Чтобы определить массу некоторого тела, нужно сравнить её с массой тела, принятого за эталон массы (или сравнить с телом уже известной массы). Масса – величина аддитивная(масса тела равна сумме масс частей, составляющих это тело). Система тел, взаимодействующих только между собой, называется замкнутой. Рассмотрим замкнутую систему тел массами 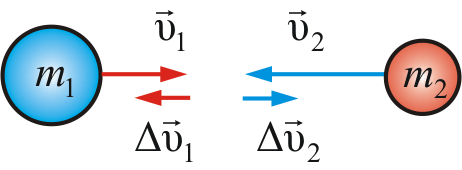 Рис. 3.1 Столкнём эти два тела. Опыт показывает, что приращённые скорости (тело, обладающее большей массой, меньше изменяет скорость). Приняв во внимание направление скоростей, запишем: При Произведение массы тела m на скорость 3.3. Второй закон Ньютона. Принцип суперпозицииМатематическое выражение второго закона Ньютона: скорость изменения импульса тела равна действующей на него силе. Отсюда можно заключить, что Из (3.3.1) получим выражение второго закона через ускорение a: Это привычная запись второго закона Ньютона, или основное уравнение динамики поступательного движения материальной точки. Принцип суперпозиции, или принцип независимости действия сил Силы в механике подчиняются принципу суперпозиции. Если на материальное тело действуют несколько сил, торезультирующую силу Из второго закона Ньютона имеем: 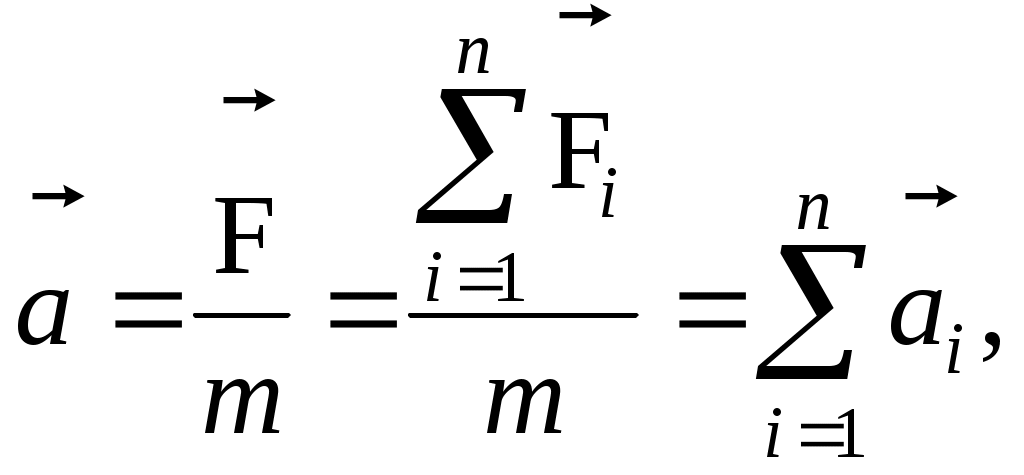 где Если на материальную точку действует несколько сил, то каждая из них сообщает точке такое же ускорение, как если бы других сил не было. Найдем изменение импульса тела за конечный промежуток времени 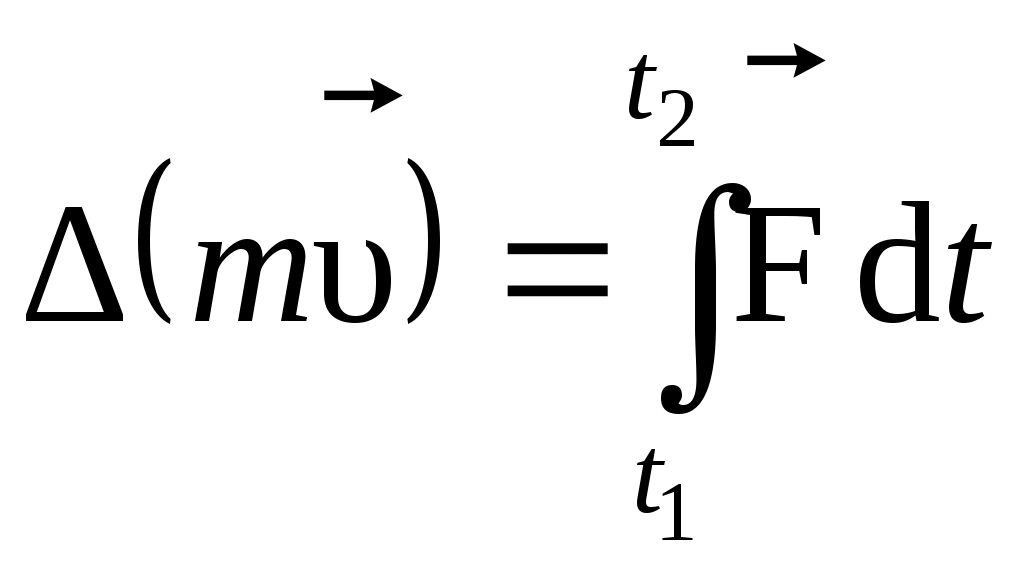 , (3.3.5) , (3.3.5)т.е., изменение импульса тела равно импульсу силы. В системе СИ семь основных единиц (см. приложение): метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), кандела (кд), единица количества вещества (моль). Остальные единицы называются производными и получаются из физических законов, связывающих их с основными единицами. Например из второго закона Ньютона производная единица силы получается равной 1 кг·м/с2, что соответствует 1 Н. 3.4. Третий закон НьютонаДействие тел друг на друга носит характер взаимодействия. Третий закон Ньютона отражает тот факт, что сила есть результат взаимодействия тел, и устанавливает, что силы, с которыми действуют друг на друга два тела, равны по величине и противоположны по направлению: Однако, третий закон справедлив не всегда. Он выполняется в случае контактных взаимодействий, т.е. при соприкосновении тел, а также при взаимодействии тел, находящихся на расстоянии друг от друга, но покоящихся друг относительно друга. Законы Ньютона плохо работают при 3.5. Импульс произвольной системы телЦентром инерции, или центром масс, системы материальных точек называют такую точку С (рис. 3.2), радиус-вектор которой: 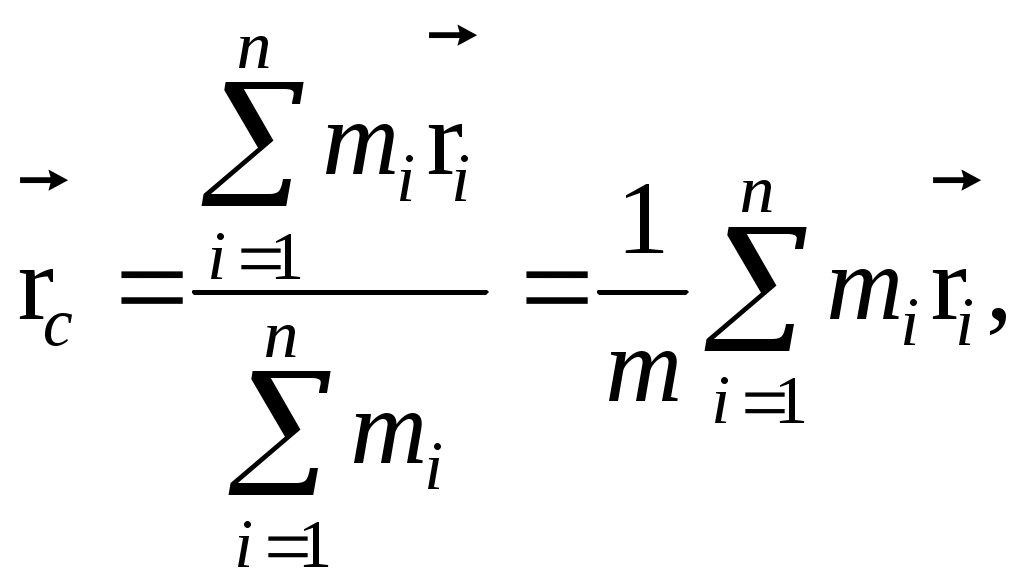 (3.5.1) (3.5.1)где 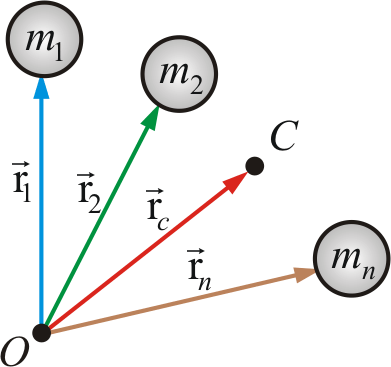 Рис. 3.2 При этом не надо путать центр масс с центром тяжести системы – с точкой приложения равнодействующей сил тяжести всех тел системы. Центр тяжести совпадает с центром масс (центром инерции), если g (ускорение силы тяжести) для всех тел системы одинаково (когда размеры системы гораздо меньше размеров Земли). Скорость центра инерции системы Здесь – импульс системы тел, то импульс системы тел можно определить по формуле – импульс системы тел равен произведению массы системы на скорость её центра инерции. 3.6. Основное уравнение динамики поступательногодвижения произвольной системы телТела, не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, – внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами. Результирующая всех внутренних сил, действующих на i-е тело: где Обозначим По второму закону Ньютона можно записать систему уравнений: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Сложим эти уравнения и сгруппируем попарно силы По третьему закону Ньютона, Назовем Скорость изменения импульса системы равна главному вектору всех внешних сил, действующих на эту систему. Это уравнение называют основным уравнением динамики поступательного движения системы тел. Так как импульс системы Отсюда можно по-другому записать основное уравнение динамики поступательного движения системы тел: здесь Центр механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе. На основании третьего закона Ньютона, силы, действующие на тела системы со стороны других тел системы (внутренние силы), взаимно компенсируют друг друга. Остаются только внешние силы. В общем случае движение тела можно рассматривать как сумму двух движений: поступательного со скоростью 3.7. Закон сохранения импульсаМеханическая система называется замкнутой(или изолированной), если на неё не действуют внешние силы, т.е. она не взаимодействует с внешними телами. Строго говоря, каждая реальная система тел всегда незамкнута, т.к. подвержена, как минимум, воздействию гравитационных сил. Однако, если внутренние силы гораздо больше внешних, то такую систему можно считать замкнутой (например, Солнечная система). Для замкнутой системы равнодействующий вектор внешних сил тождественно равен нулю: отсюда Это есть закон сохранения импульса: импульс замкнутой системы не изменяется во времени. Импульс системы тел может быть представлен в виде произведения суммарной массы тел на скорость центра инерции: При любых процессах, происходящих в замкнутых системах, скорость центра инерции сохраняется неизменной. Закон сохранения импульса является одним из фундаментальных законов природы. Он был получен как следствие законов Ньютона, но он справедлив и для микрочастиц, и для релятивистских скоростей, когда Если система незамкнута, но главный вектор внешних сил 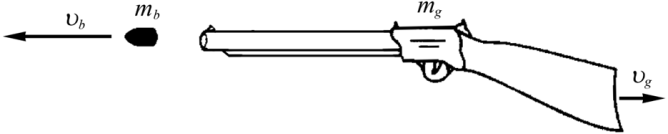 Рис. 3.3  Рис. 3.4 Рис. 3.4Для заметок ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ _____________________________________________________________________________________________________________________________________________________________________________________________________________________________ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
