|
|
дв. Задания (1). Линейная и векторная алгебра. Аналитическая геометрия
Тесты
№
|
Задание
|
Ответ
|
1.
|
При каком значении параметра 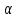 однородная система линейных однородная система линейных
уравнений имеет ненулевое решение 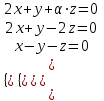
|
1) -2
2) 2
3) 1
4) -1
5) 3
|
2.
|
Решите матричное уравнение
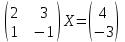
|
1) 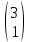 2) 2) 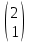 3) 3) 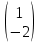 4) 4) 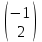 5) 5) 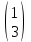
|
Тема: «Линейная и векторная алгебра. Аналитическая геометрия»
3.
|
Найдите ранг матрицы 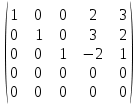
|
1) 3
2) 2
3) 1
4) 5
5) 4
|
4.
|
Выберите верную формулу
1) 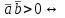 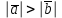
2) 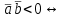 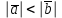
3) 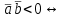 угол между векторами угол между векторами 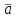 и и 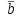 острый острый
4) 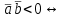 угол между векторами угол между векторами 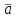 и и 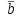 тупой тупой
5) 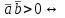 вектора вектора 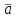 и и 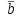 противоположно направлены. противоположно направлены.
|
1) 3
2) 2
3) 1
4) 5
5) 4
|
5.
|
Даны вектора 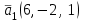 и и 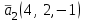 . .
Вычислите 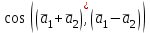 . .
|
1) 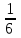 2) 2) 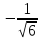 3) 3) 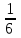
4) 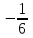 5) 5) 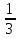
|
6.
|
Даны векторы 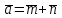 , , 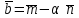 , где , где 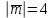 , , 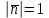 , , 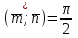 . При каком значении . При каком значении 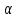 векторы векторы 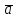 и и 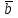 будут перпендикулярны? будут перпендикулярны?
|
1) 0 2) 16 3) 4
4) 8 5) 2
|
7.
|
Найти точку пересечения прямой 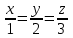 с плоскостью с плоскостью 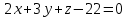 . .
|
1) (1; 2; 3) 2) (2; 4; 6) 3) (4; 8; 12)
4) (-2;-4;-6) 5) (-1;-2;-3)
|
8.
|
При каких значениях параметра 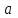 прямые на плоскости прямые на плоскости 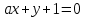 , , 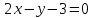 , заданные в указанном порядке, образуют угол в 45о, отсчитываемый от первой прямой против хода часовой стрелки? , заданные в указанном порядке, образуют угол в 45о, отсчитываемый от первой прямой против хода часовой стрелки?
|
1) 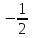 2) 2) 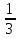 3)1 3)1
4) 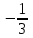 5) 2 5) 2
|
9.
|
Среди уравнений 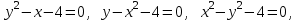
 указать уравнение гиперболы с действительной осью указать уравнение гиперболы с действительной осью 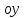 . .
|
1) 1 2) 3
3) 4 4) 2
5) 5
|
10.
|
При каких значениях параметра 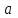 прямые в пространстве прямые в пространстве 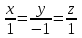 , ,
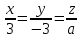 будут параллельны? будут параллельны?
|
1) -2
2) -3
3) 2
4) 3
5) 1
|
Тема: «Дифференциальное исчисление функции одной переменной»
№
|
Задание
|
Ответ
|
1..
|
Найдите предел функции 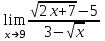 . .
|
1) 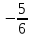 2) 2) 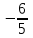 3) 3) 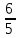 4) 4) 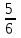 5) 2 5) 2
|
2.
|
Материальная точка движется по закону 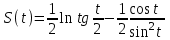 , где , где 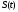 - величина пройденного пути за время - величина пройденного пути за время  . Найдите скорость движения точки в момент времени . Найдите скорость движения точки в момент времени 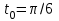 . .
|
1) 1/8 2) 4
3) 2 4) 16
5) 8
|
3.
|
Найдите наибольшее и наименьшее значение функции 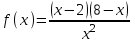 на отрезке [1;5]. на отрезке [1;5].
|
1)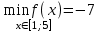 , , 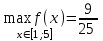 2) 2)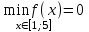 , , 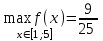
3) 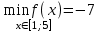 , , 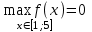 4) 4)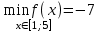 , , 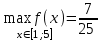
5) 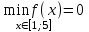 , , 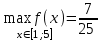
|
5.
|
Найдите предел функции 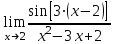 . .
|
1) 0 2) 2 3) 1 4) 1/3 5) 3
|
6.
|
Найдите наклонные асимптоты графика функции 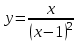 . .
|
1) 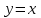 при при 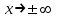 2) 2) 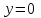 при при 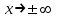
3) 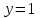 при при 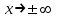 4) 4) 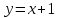 при при 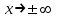
5) 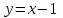 при при 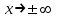
| |
|
|
 Скачать 108.67 Kb.
Скачать 108.67 Kb.