ооооо. Линейная модель множественной регрессии
 Скачать 69.11 Kb. Скачать 69.11 Kb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего образования «ФинансоВЫЙ УНИВЕРСИТЕТ при Правительстве Российской Федерации» (Финансовый университет) Департамент математики Домашняя Контрольная работа по дисциплине «Эконометрические исследования» на тему: «Линейная модель множественной регрессии» Выполнил: студент группы БА21-1м Акбашев А.Д. Проверил: к.э.н., доцент Данеев О.В. Оценка: _____________________________ Москва – 2022 Цель данной работы оценить линейную модель множественной регрессии. В работе будет проведено: Проверка адекватности модели Проверка значимости регрессеров Проверка выполнения предпосылок теоремы Гаусса-Маркова на гомоскедастичность и отсутствие автокорреляции. Анализ был проведен в MS Excel. Для работы были подобранны данные о влиянии на урожайность зерновых культур количества тракторов приведенной мощности на 100 га, количества зерно-уборочных комбайнов на 100 га, количества удобрений, расходуемых на 1 га и количества химических средств защиты на 1 га.
В первую очередь был проведен анализ на адекватность модели с константой и без неё. Была использована функция «линейн» для обоих случаев. Для модели с константой ( 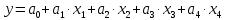 ) были получены следующие данные: ) были получены следующие данные:
Для проверки было посчитано прогнозное значение, далее посчитана разница между Y последнего значения и прогнозным. Полученный результат сравниваем с СКО, в данном случае СКО < Разницы, следовательно модель неадекватна. То же самое было сделано для модели без константы ( 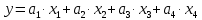 ) и были получены следующие результаты: ) и были получены следующие результаты:
В этом случае получается обратный результат СКО > Разницы, что говорит нам о том, что модель адекватна. Как стало понятно из предыдущих расчетов, для анализа была взята модель без константы. Далее проверяем значимость полученного уравнения регрессии. С помощью той же функции «линейн» получаем следующие результаты:
F критическое при = 0,05, m = 4, n=15, const = 0 составляет 3,36. Сравниваем F-тест и F-критическое и видим, что первое больше второго, а это значит, что уравнение регрессии статистически значимо. Далее проверяем значимость всех коэффициентов регрессии. Были посчитаны t для всех коэффициентов по формуле: 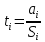 t-критическое = 2,2 ( при = 0,05, m = 4, n=15, const = 0)
Все полученные t сравниваем с t-критическое и делаем выводы, что все Х кроме 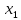 статистически значимы, так как они больше, чем t-критическое. статистически значимы, так как они больше, чем t-критическое.После этого были найдены доверительные интервалы для коэффициентов регрессии:
Предыдущий вывод, что все коэффициенты кроме 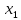 статистически значимы, так как у них 0 не попадает под интервал верхней и нижней границы. Так как статистически значимы, так как у них 0 не попадает под интервал верхней и нижней границы. Так как 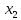 , , 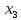 , , 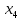 статистически значимы была построена и оценена модель для Y и этих коэффициентов: статистически значимы была построена и оценена модель для Y и этих коэффициентов:
F-критическое изменится, так как у нас поменялось количество Х и составит 3,49 (при = 0,05, m = 3, n=15, const = 0). Также сравниваем F-тест и F-критическое. F-тест больше, как и в прошлом варианте, а это значит, что уравнение регрессии статистически значимо. Далее была проведена проверка предпосылок Гаусса-Маркова. С помощью теста Голдфельда-Квандта проведена проверка на гомоскедастичность. Чтобы провести данную проверку исходные данные были разделены на 3 равные части по 5. В первой части мы получили ESS равный 0,750878, а третьей части 0,002836. Для проверки гипотезы были введены случайные переменные GQ1 = 264,8 и GQ2 = 0,004. F-критическое при при = 0,05, m = 2, n=5, const = 0 равен 161,5. F-критическое больше GQ2, но меньше чем GQ1, а это значит, что гипотеза о гомоскедастичности не выполняется соответственно модель имеет гетероскедастичность. Необходимо побороть гетероскедастичность. Для этого проведем визуальный анализ графика остатков: 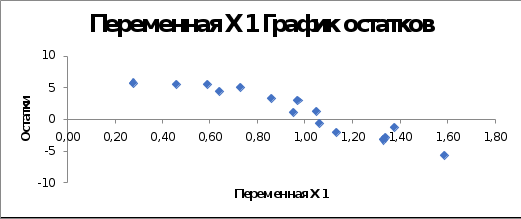 Видим, что по графику у переменной Х1 наибольший разброс, поэтому, чтобы побороть гетероскедастичность выбираем его. Для этого посчитаем дополнительные показатели:
После этого находим также ESS в первой и третьей части. ESS1 = 1,22, ESS2 = 0,61. После этого находим F-критическое и показатели GQ1 и GQ2:
F-критическое больше обоих показателей, значит условие о гомоскедастичности выполняется. Так как концентрация значений больше у первой переменной, то для В конце была проведена проверка на автокорреляцию с помощью статистки Дарбина-Уотсона. Для этого нам надо посчитать DW = 26,04/15,04 = 1,73. Значения границы при k=4 составляют 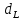 = 0,69 и = 0,69 и 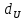 = 1,97. DW находится в области неопределенности в точке между = 1,97. DW находится в области неопределенности в точке между 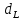 и и 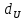 , а это значит, что нельзя определить есть автокорреляция или нет. , а это значит, что нельзя определить есть автокорреляция или нет. |
