Главная страница
Навигация по странице:

  • Индивидуальное задание

    		•

    Лабораторная работа 1 Тема: Линейная парная регрессия. Решение задач с помощью инструментов MSExcel. Лабораторная работа 1. Линейная парная регрессия. Решение задач с помощью инструментов


    Скачать 458.69 Kb.
    НазваниеЛинейная парная регрессия. Решение задач с помощью инструментов
    АнкорЛабораторная работа 1 Тема: Линейная парная регрессия. Решение задач с помощью инструментов MSExcel
    Дата15.01.2022
    Размер458.69 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная работа 1.docx
    ТипЛабораторная работа
    #331866

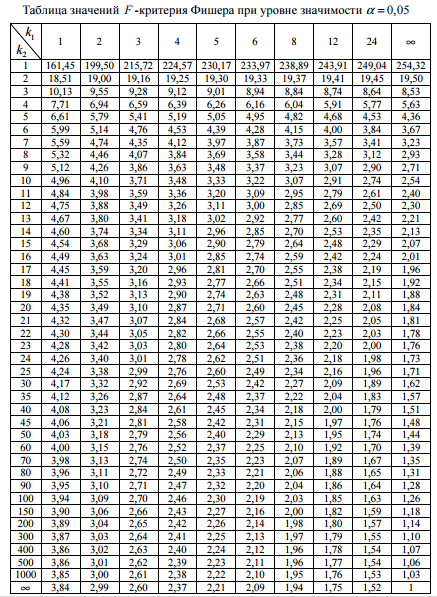
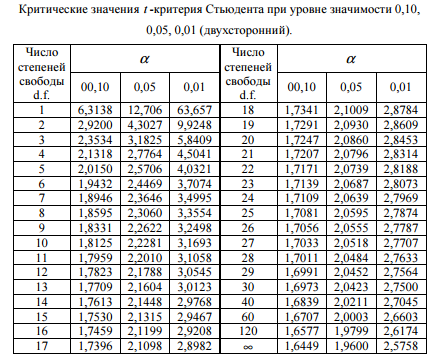
    Лабораторная работа 1

    Тема: Линейная парная регрессия. Решение задач с помощью инструментов MSExcel

    Пример. По территориям региона приводятся данные за 20ХX г.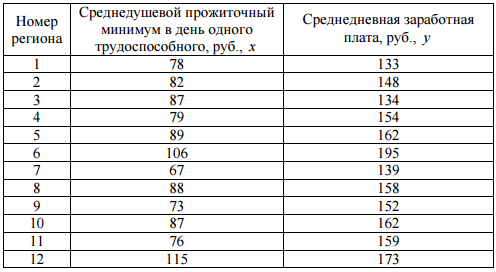



    Требуется:

    1. Построить линейное уравнение парной регрессии У по Х .

    2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации.

    3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F - критерия Фишера и t -критерия Стьюдента.

    4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x , составляющем 107% от среднего уровня.

    Решение типовой задачи в MS Excel C помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии. Если в меню сервис еще нет команды Анализ данных, то необходимо сделать следующее. В главном меню последовательно выбираем Данные → Контекстное меню на ленте → Настройка лент ы → Надстройки → Перейти и устанавливаем «флажок» в строке Пакет анализа (рис. 1):



    Рис. 1

    Далее следуем по следующему плану.

    1.После ввода исходных данных выбираем Данные →Анализ данных→Регрессия.

    2. Заполняем диалоговое окно ввода данных и параметров вывода (рис. 2):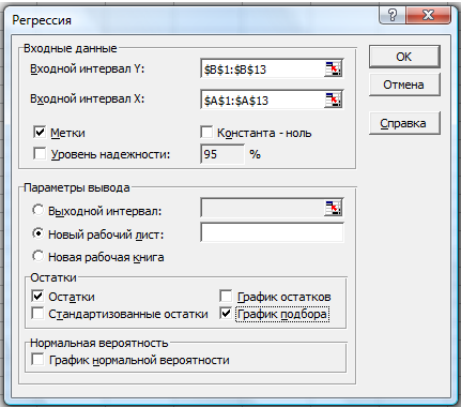



    Рис. 2

    Здесь: Входной интервал Y – диапазон, содержащий данные объясняемойпеременной;

    Входной интервал X – диапазон, содержащий данные объясняющей переменной;

    Метки – «флажок», который указывает, содержит ли первая строка названия столбцов;

    Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении;

    Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

    Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).

    Получаем следующие результаты для рассмотренного выше примера: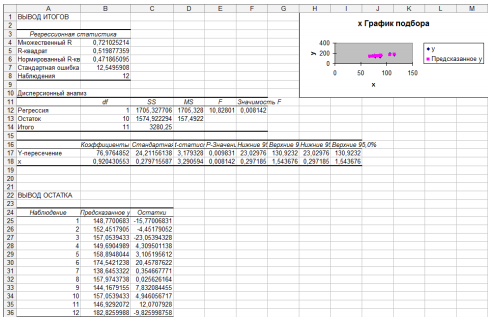



    Рис. 3

    Описание первой таблицы:

    Множественный R – коэффициент множественной корреляции.

    R-квадрат – коэффициент детерминации.

    Нормированный R-квадрат – скорректированный коэффициент детерминации.

    Стандартная ошибка – среднее квадратическое отклонение.

    Описание второй таблицы



    Описание третьей таблицы

    Данные первой строки относятся к свободному члену уравнения регрессии b0. Данные второй строки относятся к коэффициенту уравнения регрессии b1. Данные третьей строки относятся к коэффициенту уравнения регрессии b2 . И так далее в зависимости от количества объясняющих пременных.

    Столбцы таблицы:

    Первый столбец – названия коэффициентов.

    Второй столбец значения коэффициентов уравнения регрессии.

    Третий столбец – стандартная ошибка коэффициента уравнения регрессии (среднее квадратическое отклонение).

    Четвертый столбец - t-статистика для соответствующего коэффициента уравнения регрессии.
    Из таблиц выписываем, округляя до 4 знаков после запятой и переходя к нашим обозначениям:

    Уравнение регрессии:

    Коэффициент корреляции 0.7210

    Коэффициент детерминации: 0.5199 .

    Фактическое значение F -критерия Фишера: F =10,8280

    Фактические значения t -критерия Стьюдента:

    tb1=3,1793, tb2 =3,2906.

    Решить задачи в Excel. Оформить лабораторную работу.

    1. Имеются следующие данные об уровне механизации работ Х (%) и производительности труда У (т/ч) для четырнадцати однотипных предприятий:

    хi
    32
    30
    36
    40
    41
    47
    56
    54
    60
    55
    61
    67
    69
    76

    yi
    20
    24
    28
    30
    31
    33
    34
    37
    38
    40
    41
    43
    45
    48

    а) Оценить тесноту и направление связи между переменными с помощью коэффициента корреляции.

    б) Найти уравнение регрессии У по Х.

    в) Оценить качество модели с помощью коэффициента детерминации.

    г) Оценить производительность при уровне механизации 85 %.

    2. По территориям Калининградской области за 2019 год известны значения двух признаков:

    Район
    Расходы на покупку продовольственных товаров в общих расходах, % (у)
    Среднедневная заработная плата одного работающего, руб. (х)

    Калининград
    68,8
    45,1

    Гурьевский
    61,2
    59,0

    Зеленоградский
    59,9
    57,2

    Советский
    56,7
    61,8

    Светлогорский
    55,0
    58,8

    Нестеровский
    54,3
    47,2

    Балтийский
    49,3
    55,2

    Найдите уравнение регрессии У по Х и оцените тесноту и направление связи между переменными с помощью коэффициента корреляции, оценить качество модели.

    3. Решить свой вариант индивидуального задания. Вариант выбирается по номеру в списке журнала.
    Индивидуальное задание:

    Экономист, изучая зависимость уровня Y (тыс. руб.) издержек oбpaщения от объема X (тыс. руб.) товарооборота, обследовал по 10 магазинов, торгующих одинаковым ассортиментом. Полученные данные отражены в таблице по вариантам.

    Задание

    Требуется:

    • найти коэффициенты корреляции между X и Y ;

    • построить регрессионные модели зависимости Y от фактора X;

    • оценить параметры уравнения и качество уравнения с помощью коэффициента корреляции, детерминации, F-статистики и t-статистики, сделать выводы по каждому показателю;

    • используя полученное уравнение линейной регрессии, оце­нить ожидаемое среднее значение признака Y при X = 130 тыс. руб.

    Номера вариантов

    1
    2
    3
    4
    5

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    110
    6,1
    80
    4,2
    160
    12,5
    50
    4,2
    60
    2,9

    85
    4,2
    60
    4,9
    120
    9,3
    130
    10,8
    90
    7,1

    70
    2,9
    100
    7,2
    110
    9,2
    100
    9,6
    160
    1 2

    120
    5,8
    130
    9,1
    80
    6,4
    80
    5,1
    80
    6,3

    150
    8,3
    120
    6,4
    90
    7,5
    90
    7,4
    105
    7

    90
    5,2
    50
    3,9
    130
    11,6
    70
    6,2
    120
    8,4

    60
    3,4
    90
    5,1
    150
    13,1
    150
    11,4
    70
    4,8

    140
    7,5
    150
    8,4
    70
    5,2
    60
    3,3
    130
    11,2

    100
    4,9
    70
    3,5
    100
    7,9
    140
    12,2
    110
    7. 6

    115
    5,4
    125
    8,7
    60
    4,4
    110
    10,5
    140
    10,6




    Номера вариантов

    6
    7
    8
    9
    10

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    70
    2,8
    80
    4,2
    100
    3,8
    120
    4,0
    140
    5,4

    110
    3,5
    60
    4,0
    110
    4,4
    85
    3,6
    110
    4,1

    85
    2,4
    100
    4,5
    60
    3,2
    110
    4,0
    120
    5,6

    65
    2,1
    70
    3,6
    120
    4,8
    70
    2,6
    90
    3,3

    100
    3,4
    50
    3,4
    70
    3,0
    115
    4,3
    130
    4,2

    90
    3,2
    110
    5,2
    80
    3,5
    90
    3,4
    80
    2,9

    I20
    3,6
    90
    3,9
    130
    4,5
    60
    2,9
    100
    3,6

    80
    2,5
    40
    3,1
    76
    3,3
    55
    2,6
    76
    2,5

    130
    4,1
    75
    3,3
    105
    4,1
    100
    3,0
    135
    4,9

    110
    3,3
    105
    4,9
    50
    3,1
    130
    4,5
    60
    3,0




    Номера вариантов

    11
    12
    13
    14
    15

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    160
    2,8
    80
    4,2
    60
    3,8
    120
    6,1
    80
    5,4

    120
    3,5
    60
    4,9
    90
    4,4
    85
    4,2
    60
    4,1

    110
    2,4
    100
    7,2
    160
    3,2
    110
    2,9
    100
    5,6

    80
    2,1
    70
    9,1
    80
    4,8
    70
    5,8
    130
    3,3

    90
    3,4
    50
    6,4
    105
    3,0
    115
    8,3
    120
    4,2

    130
    3,2
    110
    3,9
    120
    3,5
    90
    5,2
    50
    2,9

    150
    3,6
    90
    5,1
    70
    4,5
    60
    3,4
    90
    3,6

    70
    2,5
    40
    8,4
    130
    3,3
    55
    7,5
    150
    2,5

    100
    4,1
    75
    3,5
    110
    4,1
    100
    4,9
    70
    4,9

    60
    3,3
    105
    8,7
    140
    3,1
    130
    5,4
    125
    3,0




    Номера вариантов

    16
    17
    18
    19
    20

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    70
    6,1
    80
    4,2
    100
    12,5
    50
    3,8
    140
    2,9

    110
    4,2
    60
    4,0
    110
    9,3
    130
    4,4
    110
    7,1

    85
    2,9
    100
    4,5
    60
    9,2
    100
    3,2
    120
    1 2

    65
    5,8
    130
    3,6
    120
    6,4
    80
    4,8
    90
    6,3

    100
    8,3
    120
    3,4
    70
    7,5
    90
    3,0
    130
    7

    90
    5,2
    50
    5,2
    80
    11,6
    70
    3,5
    80
    8,4

    I20
    3,4
    90
    3,9
    130
    13,1
    150
    4,5
    100
    4,8

    80
    7,5
    150
    3,1
    76
    5,2
    60
    3,3
    76
    11,2

    130
    4,9
    70
    3,3
    105
    7,9
    140
    4,1
    135
    7. 6

    110
    5,4
    125
    4,9
    50
    4,4
    110
    3,1
    60
    10,6




    Номера вариантов

    21
    22
    23
    24
    25

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    70
    4,2
    80
    2,8
    120
    3,8
    120
    4,2
    160
    4,2

    110
    4,0
    60
    3,5
    85
    4,4
    85
    4,0
    120
    10,8

    85
    4,5
    100
    2,4
    110
    3,2
    110
    4,5
    110
    9,6

    65
    3,6
    70
    2,1
    70
    4,8
    70
    3,6
    80
    5,1

    100
    3,4
    50
    3,4
    115
    3,0
    115
    3,4
    90
    7,4

    90
    5,2
    110
    3,2
    90
    3,5
    90
    5,2
    130
    6,2

    I20
    3,9
    90
    3,6
    60
    4,5
    60
    3,9
    150
    11,4

    80
    3,1
    40
    2,5
    55
    3,3
    55
    3,1
    70
    3,3

    130
    3,3
    75
    4,1
    100
    4,1
    100
    3,3
    100
    12,2

    110
    4,9
    105
    3,3
    130
    3,1
    130
    4,9
    60
    10,5




    Номера вариантов

    26
    27
    28
    29
    30

    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.
    X

    тыс. руб.
    Y

    тыс. руб.

    80
    2,8
    80
    3,2
    120
    6,1
    120
    3,5
    100
    5,2

    110
    3,5
    60
    3,6
    70
    4,2
    85
    4,5
    70
    3,4

    120
    2,4
    100
    2,5
    130
    2,9
    110
    3,3
    50
    7,5

    90
    2,1
    70
    4,1
    110
    5,8
    70
    4,1
    110
    4,9

    80
    3,4
    50
    3,3
    140
    8,3
    115
    3,1
    90
    5,4

    100
    3,2
    110
    3,4
    80
    5,4
    90
    5,2
    50
    2,9

    100
    3,6
    90
    7,5
    110
    4,1
    60
    3,4
    90
    3,6

    120
    2,5
    40
    4,9
    120
    5,6
    55
    7,5
    150
    2,5

    115
    4,1
    75
    5,4
    90
    3,3
    100
    4,9
    70
    4,9

    110
    3,3
    105
    6,3
    80
    4,2
    130
    5,4
    125
    3,0






    написать администратору сайта