ВАР. 46. Линейные электрические цепи постоянного и синусоидального тока Задача 1
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Линейные электрические цепи постоянного и синусоидального тока Задача 1.1. Линейные электрические цепи постоянного тока. Для электрической схемы, соответствующей номеру варианта и изображенной на рис. 1.3, выполнить следующее: 1.Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет (п. 2 —10) вести для упрощенной схемы. 2.Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. 3.Определить токи во всех ветвях схемы методом контурных токов. 4.Определить токи во всех ветвях схемы методом узловых потенциалов (см. указания). 5.Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. 6.Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). 7.Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора (см. указания). 8.Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС (см. указания). Значения сопротивлений, ЭДС и токов источников тока для каждого варианта даны в табл. 1.1.  Решение.   3.Определим токи во всех ветвях схемы методом контурных токов. 3.Определим токи во всех ветвях схемы методом контурных токов.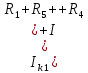 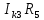 = =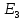 - - 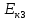 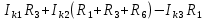 = =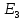 - -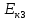 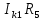 - -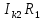 + +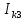 ( (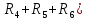 =0. =0. 38 38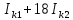 +10 +10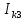 = 20 = 2018 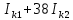 – 8 – 8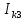 = 20 (1) = 20 (1)10 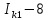 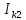 + 42 + 42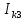 =0. =0. Систему (1) решим методом Крамера: 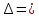 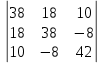 =37928, =37928,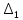 = = = -13806, = -13806, = =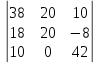 = 46507,3, = 46507,3,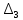 = =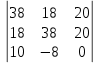 =-51870,3. =-51870,3.Итак, 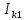 = =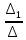 = = 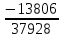 =-0,0364, =-0,0364, 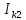 = =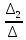 = = 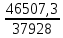 =1,2262, =1,2262,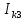 = =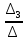 = = 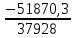 =- 1,3676. =- 1,3676.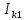 =-0,0364, =-0,0364, 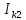 =1,2262, =1,2262,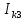 =- 1,3676– контурные токи (А). =- 1,3676– контурные токи (А).Токи в ветвях (А): 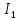 = =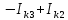 =-1,3676 + 1,2262=-0,1414, =-1,3676 + 1,2262=-0,1414,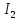 = =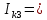 -1,3676, -1,3676,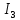 = =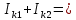 -0,0364 +1,2262 = 1,1898, -0,0364 +1,2262 = 1,1898,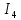 = =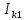 =- 0,0364, =- 0,0364,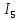 = =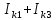 = -0,0364 +1,3676=1,3812, = -0,0364 +1,3676=1,3812,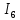 = =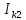 = 1,2262. = 1,2262.4.Определим токи во всех ветвях схемы методом узловых потенциалов. За нулевой потенциал примем узел b (указание к задаче). Используя обобщённый закон Ома, составим уравнения для нахождения каждого из токов (за 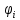 берем потенциал узла из которого ток выходит, а за берем потенциал узла из которого ток выходит, а за 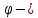 потенциал узла в который ток входит), Gi – проводимость i-ой ветви: потенциал узла в который ток входит), Gi – проводимость i-ой ветви: 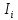 =( =(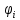 - - 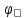 + +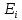 ) )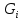 . .Соответствие узлов: узел а -1, узел в – 2, узел с – 4, узел d – 3; тогда: 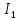 =( =(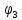 - - 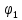 +0) +0)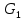 , ,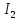 =( =(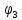 - - 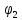 + +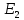 ) )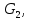 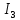 =( =(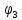 - 0 + - 0 +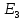 ) )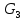 , ,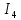 =( =(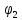 - - 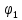 + +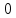 ) )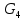 , , 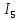 =( =(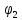 - 0 +0) - 0 +0)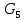 , ,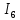 =( =(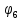 - 0 +0) - 0 +0)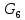 . .Подставим теперь в 1 систему Кирхгофа :  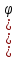 - - 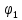 +0) +0)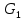 +( +(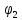 - - 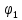 + +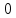 ) )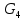 - ( - (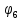 - 0 +0) - 0 +0)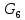 = 0 = 0( 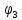 - - 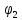 + +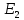 ) )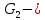 ( (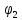 - - 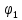 + +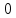 ) )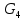 - ( - (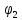 - 0 +0) - 0 +0)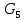 =0 =0( 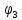 - 0 + - 0 +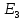 ) )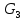 +( +(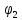 - 0 +0) - 0 +0)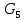 +( +(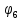 - 0 +0) - 0 +0)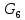 =0. =0.Приведем подобные слагаемые при различных потенциалах, получим каноническую систему уравнений. Расчет:   Система решена методом Крамера (аналогично п.3). Матрица проводимостей симметрична относительно главной диагонали. Итак: 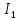 = -0,1414, = -0,1414,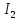 = -1,3676, = -1,3676,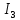 = 1,1898, = 1,1898,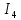 = - 0,0364, = - 0,0364,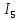 =1,3812, =1,3812,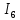 = 1,2262. = 1,2262.5.Сравним результаты расчета токов, проведенного двумя методами.
Значения токов практически совпали. 6.Составим баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Мощность источников: 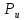 = =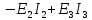 = 32*1,3676+ 29*1,1898 = 43,7632 +34,504 =78,2674Вт. = 32*1,3676+ 29*1,1898 = 43,7632 +34,504 =78,2674Вт.Мощность нагрузки: 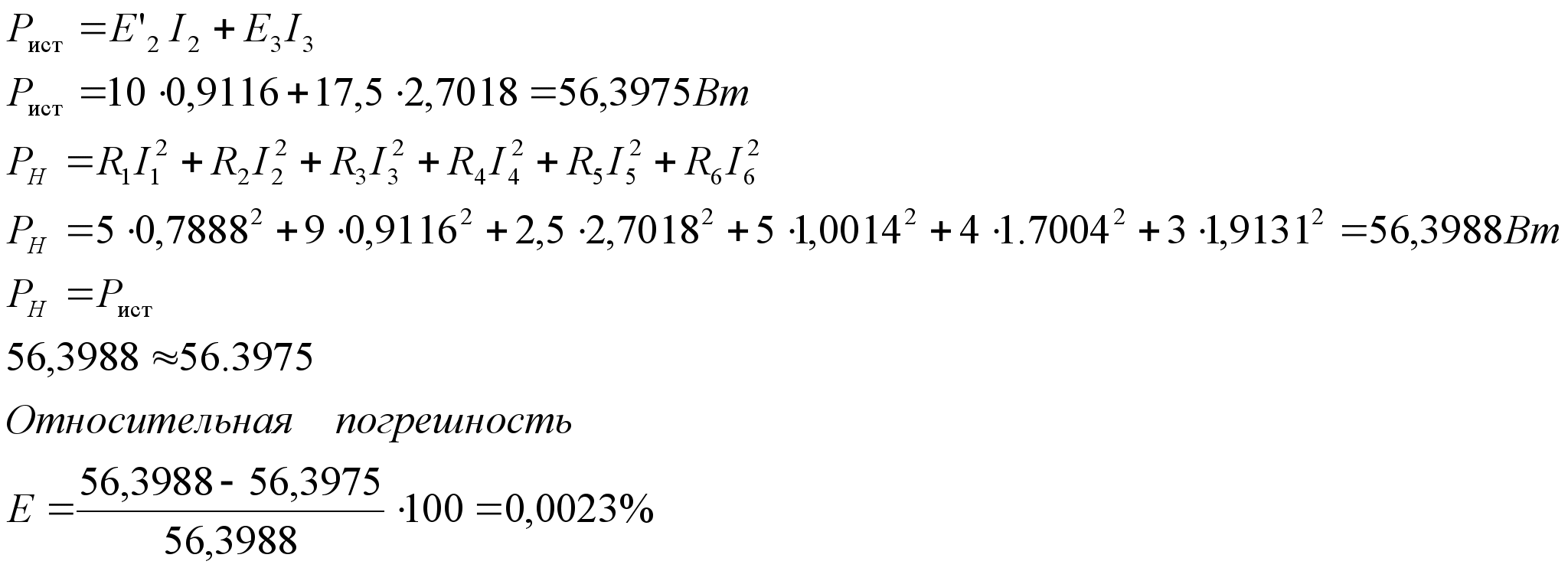 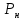 =22,4625+2,15+2,773+0,794+5,111+9,586=78,2777Вт. =22,4625+2,15+2,773+0,794+5,111+9,586=78,2777Вт.Итак: 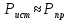 . .Погрешность: 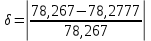 *100% = 0,013%. *100% = 0,013%.7.Определим ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора (см. указания). Определим напряжение холостого хода на зажимах разомкнутой ветви. 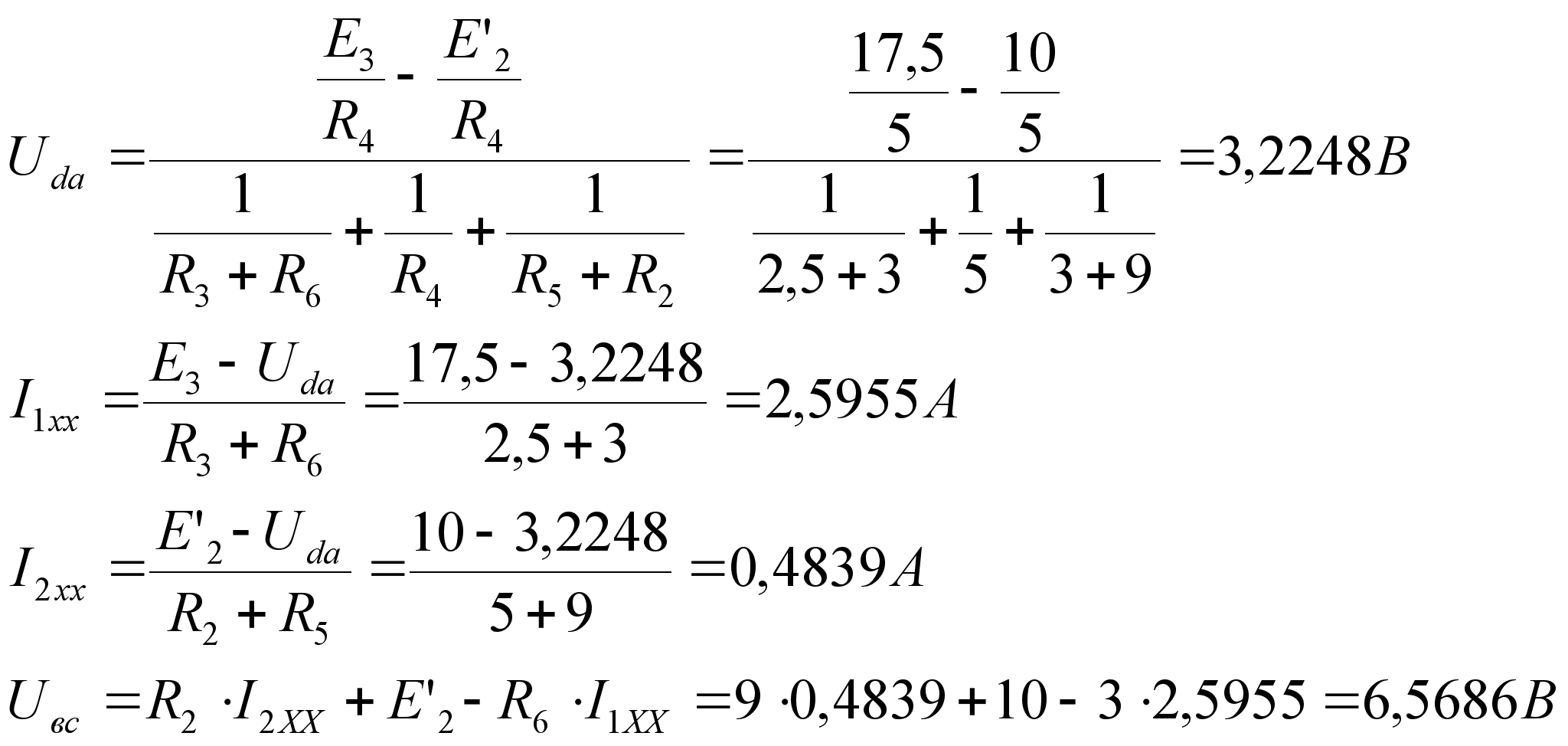           Вывод: ток, протекающий через резистор R1, найденный методом контурных токов (методом узловых потенциалов), приблизительно равен току через резистор R1, найденный методом эквивалентного генератора. Относительная погрешность составляет: 8.Начертитм потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Значения сопротивлений, ЭДС и токов источников тока для каждого варианта взяты из табл. 1.1. 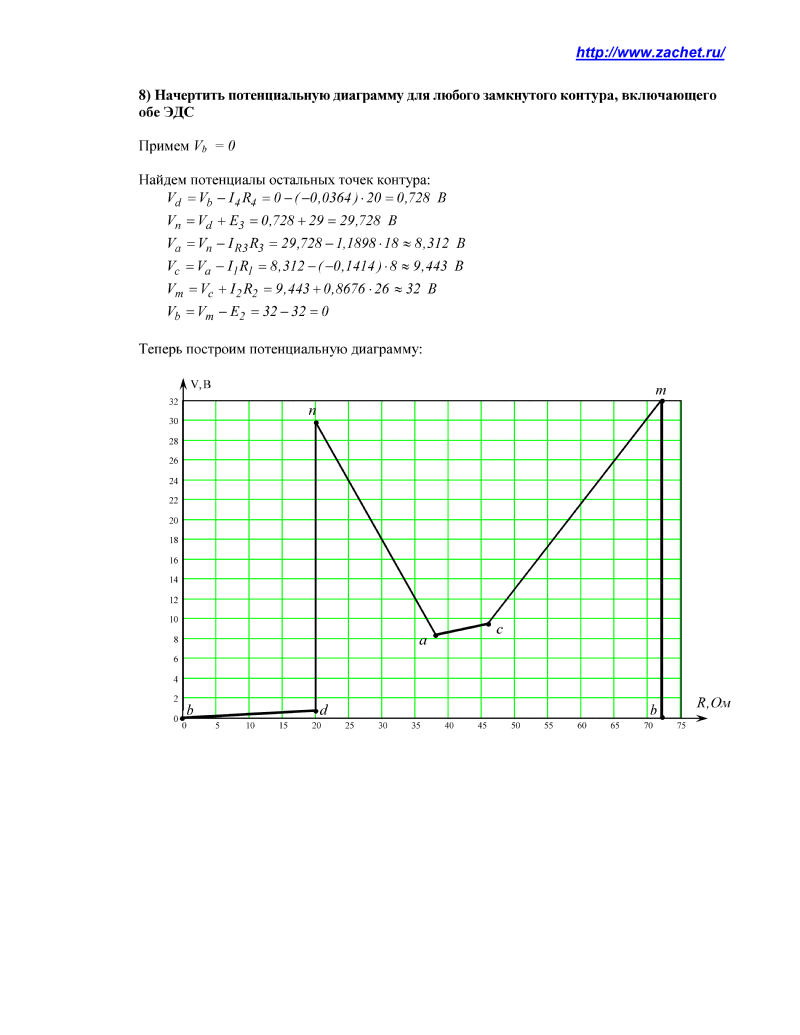 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА Задача 2 Выполнить следующее: 1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчёта токов во всех ветвях цепи, записав её в двух формах: а) дифференциальной; б) символической. 2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчёта линейных электрических цепей. При выполнении пункта 2 учесть, что одна из ЭДС в таблице может быть задана косинусоидой (не синусоидой). Чтобы правильно записать её в виде комплексного числа, сначала надо от косинусоиды перейти к синусоиде. 3. По результатам, полученным в пункте 2, составить баланс мощностей и определить показание ваттметра. 4. Построить топографическую диаграмму, совмещённую с векторной диаграммой токов. Потенциал точки а, указанной на схеме, принять равным 0. 5. Построить круговую диаграмму для тока в одном из сопротивлений цепи при изменении модуля этого сопротивления в пределах от 0 до 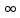 . Сопротивление, подлежащее изменению, отмечено на схеме стрелкой. . Сопротивление, подлежащее изменению, отмечено на схеме стрелкой. 6. Пользуясь круговой диаграммой, построить график изменения тока в изменяющемся сопротивлении в зависимости от модуля этого сопротивления. 7. Используя данные расчётов, полученных в пунктах 2,5 записать выражение для мгновенного значения тока или напряжения (смотри указание к выбору варианта). Построить график зависимости указанной величины от t. 8. Полагая, что между двумя любыми индуктивными катушками, расположенными в различных ветвях заданной схемы, имеется магнитная связь при взаимной индуктивности, равной М, составить в общем виде систему уравнений по законам Кирхгофа для расчёта токов во всех ветвях схемы, записав её в двух формах: а) дифференциальной; б) символической. Указания: 1. Ориентируясь на ранее принятые направления токов в ветвях, одноименные зажимы индуктивных катушек выбрать так, чтобы их включение было встречное, и обозначить на схеме точками. 2. В случае отсутствия в заданной схеме второй индуктивности, вторую катушку ввести дополнительно в одну из ветвей, не содержащих 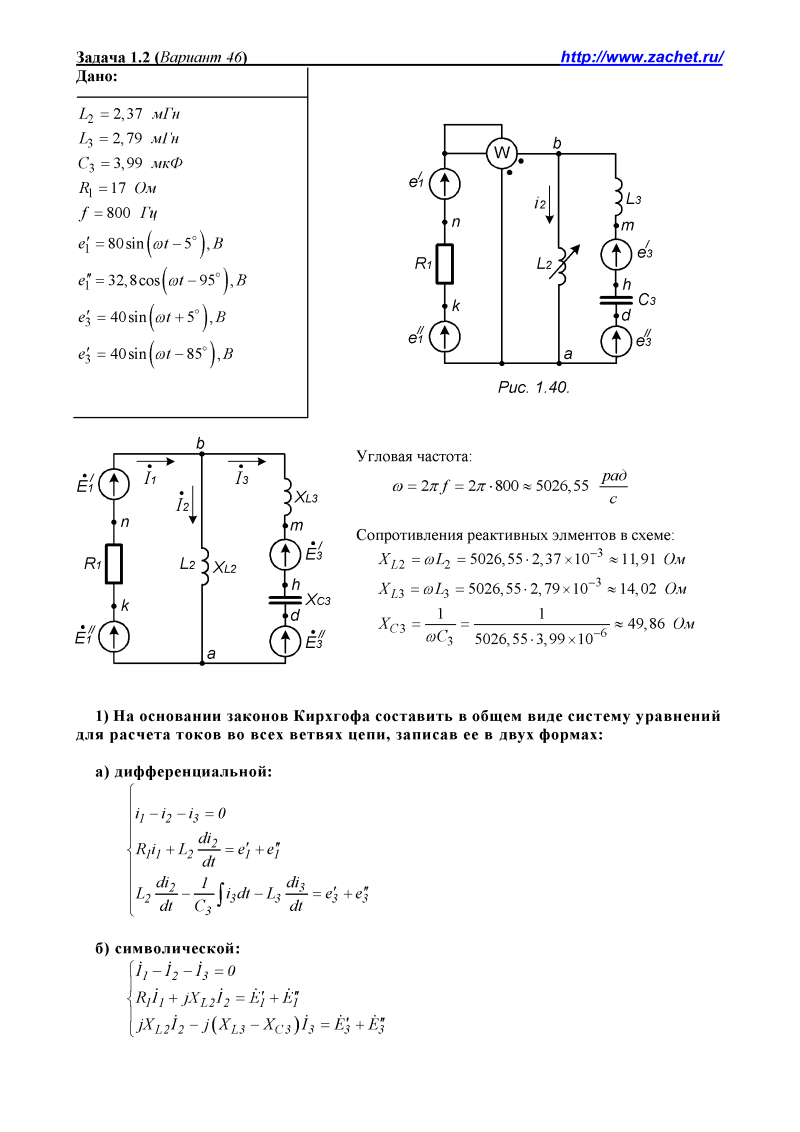 Рис. 19 (из МУ) – Исходная схема  Решение  2). Определим комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. По второму закону Кирхгофа запишем уравнение в общем виде для n-ой ветви в комплексной форме 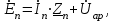 где 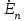 – комплексы действующих значений ЭДС n-ой ветви; – комплексы действующих значений ЭДС n-ой ветви;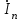 – комплекс действующего значения тока n-ой ветви, А; – комплекс действующего значения тока n-ой ветви, А;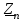 – комплексное сопротивление n-ой ветви, Ом; – комплексное сопротивление n-ой ветви, Ом;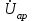 – комплекс действующего значения напряжения между узлами а и р, В. – комплекс действующего значения напряжения между узлами а и р, В. Выразим 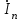 : :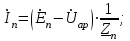 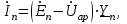 где 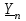 – комплексная проводимость n-ой ветви, См. – комплексная проводимость n-ой ветви, См. Запишем уравнение по первому закону Кирхгофа для узла a в комплексной форме 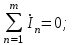 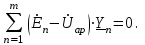 Выразим 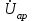 : : 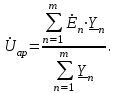  Подставив полученное значение Ůap в уравнение, сможем определить комплекс действующего значения тока в любой ветви. Для начала перейдём от мгновенных значений ЭДС к комплексам действующих значений ЭДС e = Em ∙ sin(ωt + ψe), где e – мгновенное значение ЭДС, В; Em – амплитудное значение ЭДС, В; ω∙t+ψe – текущая фаза синусоидальной ЭДС, градус. 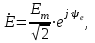 где 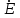 – комплекс действующего значения ЭДС, В; – комплекс действующего значения ЭДС, В; 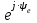 – комплексное число; – комплексное число;ψe – аргумент комплексного числа; угол между вектором и осью действительных значений. Однако ЭДС е”1 ,e’3 заданы косинусоидой. Поэтому, чтобы правильно записать её в виде комплексного числа, перейдём к синусоиде с помощью формул приведения: 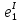 =110,5соs( =110,5соs(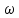 t - 90 t - 90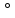 ), ), 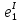 =110,5sin( =110,5sin(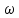 t - 90 t - 90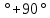 ), ), 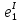 =110,5sin( =110,5sin(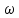 t). t).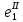 =40соs( =40соs(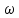 t - 90 t - 90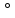 ), ), 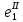 =40sin( =40sin(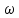 t - 90 t - 90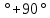 ), ), 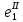 =40sin( =40sin(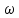 t). t).Аналогично получим: 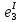 =73sin( =73sin(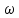 t) (по условию) и t) (по условию) и 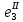 =42,3sin( =42,3sin(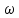 t - 90 t - 90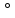 ). ).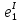 =110,5sin( =110,5sin(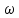 t). t). 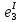 =73sin( =73sin(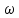 t). t).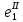 =40sin( =40sin(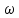 t). t). 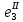 =42,3sin( =42,3sin(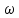 t - 90 t - 90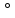 ). ). 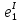 =110,5sin( =110,5sin(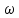 t) . t) . 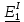 = =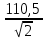 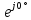 =78,93В, =78,93В,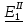 = =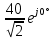 =28,57В, =28,57В,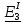 = =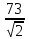 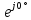 =52,14В, =52,14В,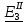 = =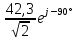 =30,21В, =30,21В,Найдём угловую частоту тока ω = 2πf, где ω – угловая частота тока, с-1; f – частота тока, Гц. Подставим числовые значения: 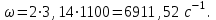 Найдём реактивные сопротивления индуктивных элементов XL = ω · L, где XL – реактивное сопротивление индуктивного элемента, Ом; L – индуктивность, Гн. XL2 = ω · L2 Подставим числовые значения: 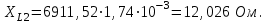 Найдём реактивные сопротивления ёмкостных элементов 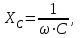 где XC – реактивное сопротивление ёмкостного элемента, Ом; С – электроёмкость, Ф. 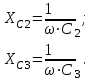 Подставим числовые значения 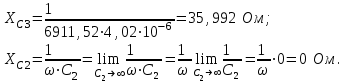 Найдём комплексные сопротивления отдельных ветвей цепи 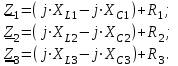 Подставим числовые значения 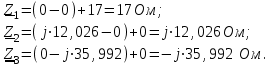 Найдём комплексные проводимости отдельных ветвей цепи 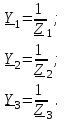 Подставим числовые значения 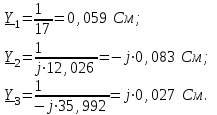 По формуле (6) найдём Ůap : 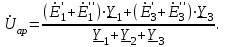 Подставим числовые значения: 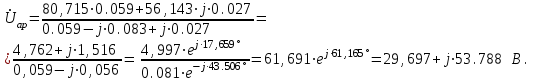 Зная числовое значение Ůap, запишем комплексы действующих значений токов ветвей данной схемы 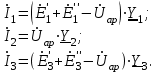 Подставим числовые значения 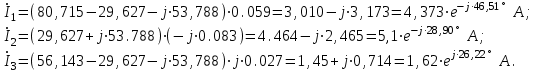 Проверка найденных токов осуществляется по первому закону Кирхгофа: 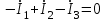 Подставим числовые значения: 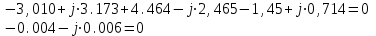 Проверка подтверждает, что искомые токи найдены правильно. 3). По результатам, полученным в п.2, определим показание ваттметра по формуле: Баланс мощностей: Sист = E1·I1* + E3·I3* = 920,1 - 58.5 jВА; Pист = 920.1 Вт; Qист = 58.5 вар (емк). Pпр = I22·R2 = 918.9 Вт; Qпр = 4.11*4,11(5.98 - 70.17) + 6.54*6,5424.01=-57.4 вар. Погрешность расчета: 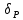 = =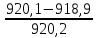 100% = 0,1%, 100% = 0,1%,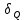 = =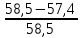 100% = 0,2%. 100% = 0,2%.4). Построим топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал точки а, указанной на схеме, примем равным нулю. Векторная диаграмма токов представляет изображение всех токов на комплексной плоскости. Для построения топографической диаграммы необходимо определить геометрическое место потенциала каждой точки на комплексной плоскости. Находим потенциалы точек. Для этого примем: ; тогда: ; ; . Для построения выбираем масштаб по осям. Он должен быть одинаковым. Пусть будет 1 А./дел. Наносим рассчитанные вектора токов на комплексную плоскость в соответствии с выбранным масштабом. Первый закон Кирхгофа в векторной форме сходится. Далее выбираем масштаб по осям для потенциалов и наносим на эту же плоскость точки потенциалов . 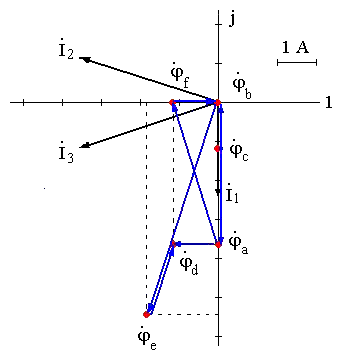 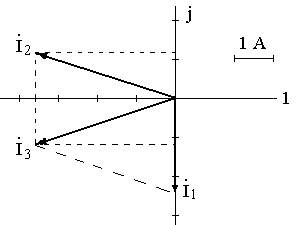 Рис. 1 – Векторная диаграмма Рис. 2 –Топографическая диаграмма 5. Построим круговую диаграмму для тока в одном из сопротивлений цепи при изменении модуля этого сопротивления в пределах от 0 до  . Сопротивление, подлежащее изменению, отмечено на схеме стрелкой. Круговая диаграмма – это окружность, по которой перемещается конец вектора тока при изменении сопротивления одной из ветвей схемы (на схеме обозначено стрелкой). Для построения круговой диаграммы определим параметры эквивалентного генератора. Для этого из схемы исключим переменный элемент, а на оставшихся зажимах проставим напряжение холостого хода Uхх по направлению, совпадающему с током I1. . Сопротивление, подлежащее изменению, отмечено на схеме стрелкой. Круговая диаграмма – это окружность, по которой перемещается конец вектора тока при изменении сопротивления одной из ветвей схемы (на схеме обозначено стрелкой). Для построения круговой диаграммы определим параметры эквивалентного генератора. Для этого из схемы исключим переменный элемент, а на оставшихся зажимах проставим напряжение холостого хода Uхх по направлению, совпадающему с током I1. В измененной схеме протекает только один ток I’. Найдем его значение, используя второй закон Кирхгофа. Для определения Uxx составим уравнение по второму закону Кирхгофа для любого контура, включающего Uxx. В окружности хорда равна Ik = 14.53*e12.8 ; коэффициент равен k=0.36; вписанный угол = - 7. 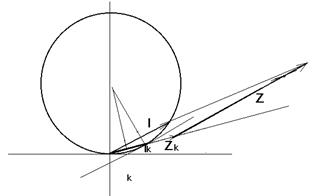 Рис. 3 – Круговая диаграмма 6).Пользуясь круговой диаграммой построим график изменения этого тока в зависимости от модуля сопротивления. Запишем выражение для мгновенного значения напряжения холостого хода Uxx: Модуль действующего значения напряжения холостого хода: Амплитудное значение напряжения холостого хода: Определим начальную фазу Uxx: Мгновенное значение напряжения холостого хода: 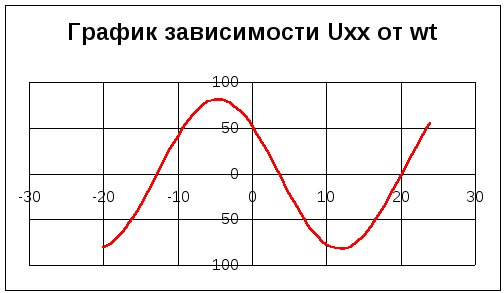 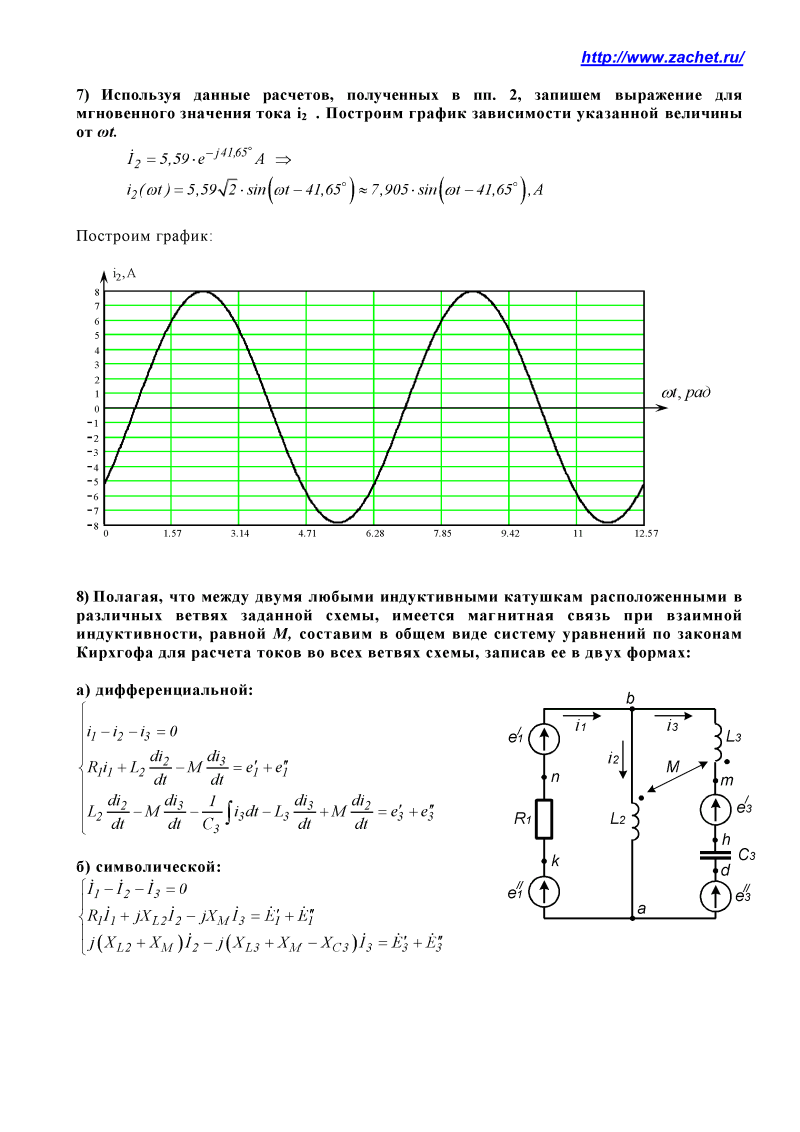 ЛИТЕРАТУРА 1.Электротехника / Под ред. В.Г. Герасимова. – М: Высшая школа, 1985. 2.Электротехника. Программированное, учебное пособие / Под ред. В.Г. Герасимова. – М.: Высшая школа, 1983. 3.Сборник задач по электротехнике и основам электроники / Под ред. В.С. Пантюшина. – М.: Высшая школа, 1979. 4.Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. – М.: Энергия, 1984. 5.Основы промышленной электроники / Под ред. В.Г. Герасимова, – М.: Высшая школа, 1978. 6.Лабораторные работы по электротехнике / Под ред. В.С. Пантюшина. – М.: Высшая школа, 1977. |
