Зразок ЛЗ 2 ПК Лінійні конгруенції за простим та складеним модул. Лінійні конгруенції за простим та складеним модулем
 Скачать 235.76 Kb. Скачать 235.76 Kb.
|
|
Київський університет імені Бориса Грінченка Факультет інформаційних технологій та управління Кафедра інформаційної та кібернетичної безпеки З В І Т з лабораторної роботи № 2 з дисципліни ”Прикладна криптологія“ Тема: Лінійні конгруенції за простим та складеним модулем Варіант № 0 Виконав(ла): студент(ка) групи _______Прізвище І.Б.________________________ Дата здачі/захисту____________________ Перевірив___________________________ Оцінка______________________________ 20__ Виконання роботи Завдання 1. Розв'язати конгруенцію 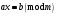 із застосуванням із застосуванням1) способу Ейлера; 2) способу застосування розширеного алгоритму Евкліда; 3) загального способу. 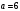 , , 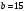 , , 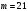 Розв’язання. Розв’яжемо конгруенцію 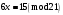 . .І спосіб (спосіб Ейлера). Оскільки 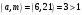 , то конгруенція , то конгруенція 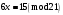 має три розв’язки. має три розв’язки.Розділимо обидві частини конгруенції і модуль на 3. Отримаємо еквівалентну конгруенцію: 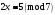 . .Оскільки 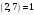 , то дана конгруенція має єдиний розв’язок. Знаходимо його за формулою , то дана конгруенція має єдиний розв’язок. Знаходимо його за формулою 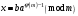 : :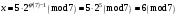 . .Отже, розв’язком конгруенції 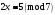 буде буде 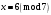 і весь клас лишків і весь клас лишків 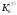 . За модулем . За модулем 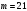 цей клас розпадеться на три класи: цей клас розпадеться на три класи: 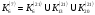 , які є розв’язками початкової конгруенції. , які є розв’язками початкової конгруенції.Відповідь. Розв’язками лінійної конгруенції 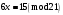 є класи є класи 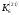 , , 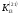 , , 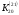 . .Перевірка. 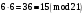 . .ІІ спосіб (за допомогою розширеного алгоритму Евкліда). Оскільки 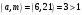 , то конгруенція , то конгруенція 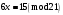 має три розв’язки. має три розв’язки.Розділимо обидві частини конгруенції і модуль на 3. Отримаємо еквівалентну конгруенцію: 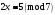 . .Оскільки 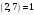 , то дана конгруенція має єдиний розв’язок: , то дана конгруенція має єдиний розв’язок: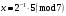 . .За допомогою розширеного алгоритму Евкліда знайдемо число, обернене до 2 за модулем 7. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
Маємо 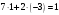 , звідки , звідки 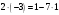 . Отже . Отже 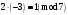 , тому , тому 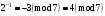 . Таким чином . Таким чином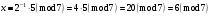 . .і розв’язком конгруенції 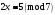 буде буде 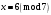 і весь клас лишків і весь клас лишків 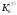 . За модулем . За модулем 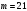 цей клас розпадеться на три класи: цей клас розпадеться на три класи: 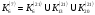 , які є розв’язками початкової конгруенції. , які є розв’язками початкової конгруенції.Відповідь. Розв’язками лінійної конгруенції 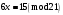 є класи є класи 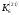 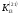 , ,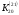 . .Перевірка. 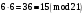 . .ІІІ спосіб (застосування загального алгоритму розв’язування лінійної конгруенції). Розв’яжемо відповідне диофантове рівняння 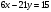 . .Застосуємо розширений алгоритм Евкліда до чисел 6 і 21. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
Таким чином, 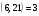 . .Рівняння розв’язуване, оскільки 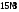 . Оскільки . Оскільки 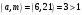 , то конгруенція , то конгруенція 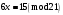 має три розв’язки. З лінійного представлення має три розв’язки. З лінійного представлення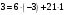 маємо 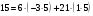 ; ;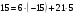 Візьмемо 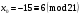 . Згідно теоремі про розв’язуваність лінійної конгруенції існують . Згідно теоремі про розв’язуваність лінійної конгруенції існують 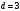 класів розв’язків, які можна отримати з класів розв’язків, які можна отримати з 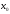 зсувом на зсувом на 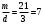 : :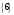 , , 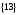 , , 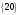 або 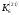 , , 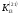 , , 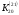 . .Відповідь. Розв’язками лінійної конгруенції 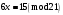 є класи є класи 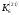 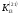 , ,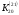 . .Перевірка. 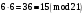 . .Завдання 2. Розв'язати конгруенцію 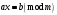 за допомогою китайської теореми про остачі, виходячи з відомої факторизації модуля. за допомогою китайської теореми про остачі, виходячи з відомої факторизації модуля.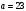 , , 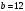 , , 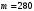 . .Розв’язання. Конгруенція 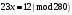 , , 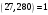 , , 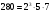 , еквівалентна системі конгруенцій , еквівалентна системі конгруенцій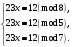 або або 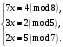 або або 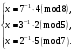 Знайдемо в кожній конгруенції системи обернене число за відповідним модулем. 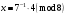 Оскільки 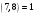 , то клас лишків, обернений до класу , то клас лишків, обернений до класу 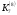 , існує. Застосуємо розширений алгоритм Евкліда до чисел 7 і 8. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці: , існує. Застосуємо розширений алгоритм Евкліда до чисел 7 і 8. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
Маємо 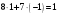 , звідки , звідки 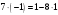 . Отже, . Отже, 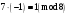 , тому , тому 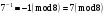 . Таким чином, . Таким чином,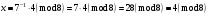 . .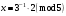 Оскільки 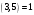 , то клас лишків, обернений до класу , то клас лишків, обернений до класу 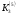 , існує. Застосуємо розширений алгоритм Евкліда до чисел 3 і 5. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці: , існує. Застосуємо розширений алгоритм Евкліда до чисел 3 і 5. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
Маємо 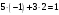 , звідки , звідки 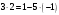 . Отже, . Отже, 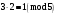 , тому , тому 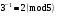 . Таким чином, . Таким чином,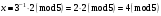 . .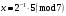 Оскільки 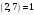 , то клас лишків, обернений до класу , то клас лишків, обернений до класу 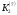 існує. Застосуємо розширений алгоритм Евкліда до чисел 2 і 7. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці: існує. Застосуємо розширений алгоритм Евкліда до чисел 2 і 7. Протокол роботи розширеного алгоритму Евкліда оформимо у вигляді таблиці:
Маємо 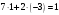 , звідки , звідки 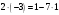 . Отже, . Отже, 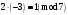 , тому , тому 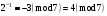 . Таким чином, . Таким чином,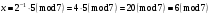 . .Таким чином, маємо систему конгруенцій 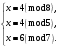 Оскільки всі модулі попарно взаємно прості, застосуємо китайську теорему про остачі. Згідно позначенням китайської теореми про остачі, маємо: 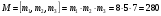 ; ;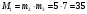 ; ;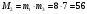 ; ;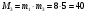 ; ;Знайдемо число, обернене до 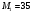 за модулем за модулем 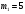 , тобто таке, що , тобто таке, що 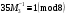 . .Застосуємо розширений алгоритм Евкліда до чисел 35 і 8. Протокол роботи розширеного алгоритму Евкліда запишемо у вигляді таблиці:
Таким чином 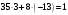 . .Звідси 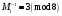 . .Знайдемо число, обернене до 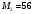 за модулем за модулем 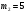 , тобто таке, що , тобто таке, що 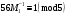 . .Застосуємо розширений алгоритм Евкліда до чисел 56 і 5. Протокол роботи розширеного алгоритму Евкліда запишемо у вигляді таблиці:
Таким чином, 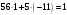 . .Звідси 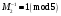 . .Знайдемо число, обернене до 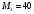 за модулем за модулем 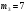 , тобто таке, що , тобто таке, що 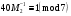 Застосуємо розширений алгоритм Евкліда до чисел 40 і 7. Протокол роботи розширеного алгоритму Евкліда запишемо у вигляді таблиці:
Таким чином 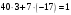 . .Звідси 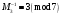 . .Тепер знаходимо розв’язок системи 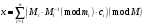 : :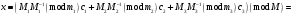 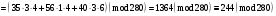 Перевірка. 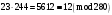 . .Завдання 3. Вкажіть число розв’язків конгруенції 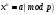 . .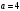 , , 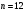 , , 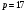 Розв’язання. Знайдемо 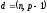 : : 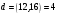 . .Перевіримо виконання умови 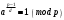 : : 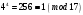 – умова виконана. Значить, конгруенція – умова виконана. Значить, конгруенція 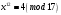 розв’язувана. Число розв’язків конгруенції дорівнює розв’язувана. Число розв’язків конгруенції дорівнює 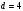 . .Відповідь: 4. |

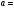 7
7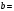 2
2