олимпиадная математика 6 класс. листок 7. Листок Длины и расстояния 1
 Скачать 21.85 Kb. Скачать 21.85 Kb.
|
|
Проверочная работа Существует ли такое натуральное число, что при умножении его на любое другое натуральное число у полученного произведения будет нечётная сумма цифр? Листок 7. Длины и расстояния 1 На стороне AC треугольника ABC отметили точку E. Известно, что периметр треугольника ABC равен 25 см, треугольника ABE — 15 см, треугольника BCE — 17 см. Найдите длину отрезка BE. 2 Отрезок, равный 28 см, разделён на три (возможно неравных) отрезка. Расстояние между серединами крайних отрезков равно 16 см. Найдите длину среднего отрезка. 3 Длина стороны AC треугольника ABC равна 3.8 см, длина стороны AB — 0.6 см. Известно, что длина BC — целое число. Чему она может быть равна? 4 Прямоугольник разбит на 9 меньших прямоугольников. Периметры четырех из них указаны на рисунке. Чему равен периметр прямоугольника x? 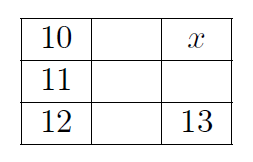 5 Квадрат ABCD со стороной 2 и квадрат DEFK со стороной 1 стоят рядом на верхней стороне AK квадрата AKLM со стороной 3. Между парами точек A и E, B и F, C и K, D и L натянуты паутинки. Паук поднимается снизу вверх по маршруту AEFB и спускается по маршруту CKDL. Какой маршрут короче? 6 Один прямоугольник расположен внутри другого. Может ли так быть, что периметр внутреннего прямоугольника больше периметра внешнего? 7 На клетчатой бумаге нарисован квадрат со стороной 5. Можно ли его разрезать на пять частей одинаковой площади, проводя разрезы только по линиям сетки так, чтобы суммарная длина разрезов была не больше 16? 8 Прямоугольник составлен из шести квадратов (см. рисунок).  Найдите сторону самого большого квадрата, если сторона самого маленького равна 1. |
