Курсовая. ВВЕДЕНИЕ2. Литература объектом исследования в работе являются методы достоверной оценки пространственного распределения удельного электрического сопротивления (уэс) в околоскважинной части терригенного разреза,

• Название: Литература объектом исследования в работе являются методы достоверной оценки пространственного распределения удельного электрического сопротивления (уэс) в околоскважинной части терригенного разреза,
• Анкор: Курсовая
• Дата: 14.09.2022
• Размер: 1.94 Mb.
• Имя файла: ВВЕДЕНИЕ2.docx
• Тип: Литература; #676448
• страница: 2 из 8

* (

О

В зарубежных видах комплексной аппаратуры DIL, DIFL, DISF, разработанных ведущими фирмами Шлюмберже, Дрессер-Атлас, Гер­харт-Оуэн, как правило, комплексируются два разноглубинных индук­ционных зонда большого и среднего радиусов исследования с зондом бокового каротажа, потенциал- или микросферическим зондом. В по-

22

следние годы за рубежом появилась многозондовая аппаратура ИК но­вого поколения, содержащая 8 трехкатушечных зондов, б из которых работают на двух частотах. Учитывая, что все зонды регистрируют од­новременно активную и реактивную составляющие сигнала, общее ко­личество кривых равно 28. Типичным примером такого типа аппарату­ры является разработанный в 1990 г. многозондовый прибор AIT, имеющий достаточно большие габариты и вес. Последней разработкой в этой области является индукционный комплекс фирмы Western Atlas. В нем одновременно регистрируются активная и реактивная компоненты в 8-ми трехкатушечных зондах на 7-и частотах (диапазон 15 - 230 кГц), общее число диаграмм равно 112 [56, 58] Для определения продольной и поперечной проводимости тонкослоистых терригенных коллекторов фирмой Baker Atlas выпускается индукционный комплекс 3DEX с измерением реактивной и активной составляющей трех компо­нент временной производной магнитной индукции. Частота тока в гене­раторе изменяется в пределах от первых десятков до первых сотен ки­логерц.

Прямых аналогов в России эти виды аппаратуры не имеют.

Наряду с развитием индукционных методов исследования удель­ной электрической проводимости пород появились и получили свое дальнейшее развитие методы электромагнитного каротажа, направлен­ные на измерение диэлектрической проницаемости пород - диэлектри­ческий (ДК) и волновой диэлектрический (ВДК) каротаж.

Диэлектрическая проницаемость горной породы зависит в основном от содержания в ней подвижной и малоподвижной воды. Поэтому по данным ДК в комплексе с данными других методов ГИС можно опреде­лять коэффициент остаточной водонасыщенности и характер насыще­ния коллекторов, а при глубоких зонах проникновения - пористость. Дополняя при решении указанных задач методы сопротивления ДК вы­годно отличается от них малой зависимостью диэлектрической прони­цаемости от минерализации воды, возможностью измерений в скважи­нах, заполненных непроводящими и малопроводящими промывочными жидкостями.

Высокочастотные методы имеют ряд преимуществ при определе­нии УЭС по сравнению с широко известными методами

Практически ДК был реализован С.М. Аксельродом и Г.Я. Черняком в 60-х годах. Ими была разработана и опробована аппа­ратура, базирующаяся на принципе скважинного конденсатора. Малая глубинность исследования, большое влияние скважины на результаты измерений и неразработанность теории явились причиной того, что эта модификация ДК не нашла широкого применения. В то же время полу­ченные результаты послужили важным стимулом для развития новых модификаций ДК.

В 1963 - 1964 гг. в Сибирском отделении АН СССР Д.С. Даевым и А.А. Кауфманом был предложен диэлектрический индуктивный каро­таж (ДИК), основанный на измерении амплитуды вторичного поля вер­тикальными магнитными диполями. Благодаря удалению измерителей поля от источника, глубинность зондов ДИК выше, чем у конденсатор­ного зонда.

В 1966 г. Д.С. Даевым предложен способ ДК, основанный на изме­рении относительных параметров поля, в частности разности фаз элек­тромагнитной волны в двух точках на оси скважины, удаленных от из­лучающей катушки. Дальнейшее развитие способ получил в направле­нии измерения нескольких относительных параметров поля. Д.С. Даеву принадлежит разработка волновой трактовки явлений в ДК, которая и позволила сформулировать способы относительных измерений. Эти способы отличаются от ДИК практически полным отсутствием влияния скважины, более благоприятными вертикальными характеристиками зондов и меньшим влиянием УЭС на результаты измерений при опре­делении е.

Теория высокочастотных электромагнитных методов исследования скважин, рассматриваемых ниже, базируется в основном на строгих решениях ряда осесимметричных задач с заданным возбудителем поля в виде вертикального магнитного диполя с гармонически меняющимся моментом.

Решение задачи о поле магнитного диполя при наличии пласта ко­нечной мощности приведено в работах Г.Н. Зверева, А.А. Кауфмана. На основе этих решений путем математического моделирования рядом ис­следователей были изучены вертикальные характеристики зондов вы­сокочастотных электромагнитных методов.

В 1971 г. Н.М. Афониной было получено решение задачи о поле вертикального магнитного диполя для модели среды с четырьмя плос­копараллельными поверхностями раздела. На основе этого решения В.С. Зинченко проведено исследование влияния пачек пластов на пока­зания зондов высокочастотных электромагнитных методов.

Для поля диполя при наличии горизонтальных границ раздела

1. 
   Д. Карийским найдены приближенные решения на базе принципов геометрической оптики. Они позволили понять физику процессов, про­исходящих при прохождении электромагнитной волны в данной модели среды.
   

Теория метода электромагнитного каротажа для цилиндрически- слоистых сред развита В.Н. Никитиной, Г.Н. Зверевым, Д.С. Даевым,

2. 
   И. Дмитриевым. На ее базе были исследованы радиальные характе­ристики зондов. Задача для модели среды с сочетанием горизонтальных и вертикальных границ раздела решена методами интегральных урав­нений (Е.В. Захаров, И.В. Ильин, Н.И. Несмеянова) и конечных разно­стей (А.Д. Карийский). Это позволило изучить влияние скважины в пластах конечной мощности, искажения поля, вносимых кавернами, со­вместное влияние скважины, зоны проникновения, конечной мощности пластов и др.
   

Параллельно с развитием теории интенсивно велись работы по созданию и опробованию аппаратуры. Была закончена разработка ап­паратуры ВИК и ВК-723 для определения УЭС; АДК-1, ДК1-713 для определения е. Проводилось широкое опробование габаритных макетов этой аппаратуры.

Успехи в области интерпретации данных высокочастотных элек­тромагнитных методов были достигнуты благодаря проведенным систе­матизированным исследованиям свойств горных пород на образцах керна (С.М. Аксельрод, Г.Я. Черняк, ЛИ. Дубман, Ю.Л. Брылкин, В.В. Лихачев, В.Н. Романов и др.), широкому опробованию методов количе­ственной интерпретации на базе зависимостей «керн-геофизика» (С.Б. Денисов, В.В. Лихачев, Я.Н. Басин, В.С. Зинченко, В.Д. Чухвичев, Ю.П. Кадысев, А.И. Костин и др.), глубокому анализу результатов ре­шений прямых задач.

С начала 70-х годов высокочастотные электромагнитные методы интенсивно развиваются рядом зарубежных нефтяных и промыслово­геофизических фирм. Так, способы ДИК, развитые на базе работ Д.С. Даева и Ю.Н. Антонова, были предложены фирмой 'Тексако" в 1973 - 1974 гг. Запатентованные ею устройства содержать трехкату­шечный зонд, измеряющий относительные характеристики магнитного поля на частоте 32 МГц зондом Г0.2Г0.8И и суммарного поля на частоте 16 МГц зондом И1.0Г, измерительные катушки — общие для обоих зондов. Спецификой аппаратурного решения является стабилизация тока в излучающей катушке зонда. Той же фирмой предложен способ определения е путем измерения суммарного поля зондом И 1.0 Г на частоте 32 МГц и кажущегося сопротивления стандартным зондом ИК на частоте 20 кГц. Последнее используется как поправка за УЭС в ре­зультаты измерений на частоте 32 МГц.

"Тексако" и позднее "Шлюмберже" реализовали способы ВДК от­личающиеся только особенностями аппаратурной реализации или при­менения. Например, в 1974 г. запатентован способ определения 8 трех­катушечным зондом, измеряющим на частоте 30 МГц разность фаз и амплитуду суммарного поля. В 1977 г. предложено устройство опреде­ления s по разности фаз и отношению амплитуд.

Фирмой "Шлюмберже" предложен способ повышения глубинности путем измерения разности фаз длинным зондом ВДК и отношение ам­

плитуд коротким зондом на частоте 32 МГц и определения по ним s горных пород.

В США запатентован применительно к ВДК способ измерения раз­ности фаз путем счета числа импульсов, поступающих на вход счетной схемы в промежуток времени между переходами через нуль сигналов в первой и второй измерительных катушках зонда [56]. В скважинном приборе зондом И0.2И0.8Г на частоте 47 МГц измеряются разность фаз и амплитуды ЭДС в измерительных катушках. Вычисление отношения амплитуд производится на поверхности.

Способ микроволнового диэлектрического каротажа разрабатывал­ся только фирмой "Шлюмберже". Фирменное название - EPL (electro­magnetic propagation log). Способ заключается в измерении времени прохождения и затухания электромагнитной волны частотой 1-3 ГГц на интервале базы зонда (И 0.04 И 0.08 Г) [57].

Имеется целый ряд патентов США 1976 - 1979 гг. на применение способа для определения е и к_ш оценки наличия адсорбированной воды. Для исключения влияния каверн коэффициент затухания и фазовую постоянную измеряют симметричным зондом, имеющим две измери­тельные и две излучающие катушки, расположенные по разные сторо­ны от приемных. Излучающие катушки включаются поочередно. Ре­зультат измерений — полусуммы значений, найденные при включен­ных верхнем и нижнем излучателях.

Фирмой "Эксон" в 1975 г. предложен способ определения диэлек­трической проницаемости пород в ближней и дальней от стенки сква­жины зонах путем измерения переходного процесса с помощью двух­электродного зонда, электроды которого гальванически соединены со стенкой скважины.

Эффективность применения геофизической аппаратуры, возмож­ность использования результатов измерений для массовых количест­венных и качественных определений свойств горных пород непосредст­венно связаны с возможностью сопоставления диаграмм и обработан­ных данных при известной точности измерений. Сложность задачи по­

строения систем метрологической поверки заключена в противоречиво­сти самой постановки задачи - обеспечить высокую точность простыми и надежными средствами. Для метрологического обеспечения исполь­зуются средства измерений, заимствованные из государственных повероч­ных схем: исходные образцовые средства измерений и образцовые средства измерений [13]. Средства измерений, заимствованные из госу­дарственных поверочных схем, используют для метрологической аттеста­ции исходных образцовых средств и определения отдельных характери­стик средств измерений. В качестве исходных образцовых средств измере­ния в поверочных схемах для скважинных средств измерения УЭС час­то применяют стандартные образцы УЭС, выполненные в виде емко­стей, заполненных водой. Причем влияние краевых эффектов на пока­зания поверяемой аппаратуры не должно превышать 0.2 % (РДС 39-01­031-80). Предел основной допускаемой относительной погрешности исход­ных образцовых средств измерения установлен 0.8 %. С помощью ис­ходных образцовых средств измерения аттестуют образцовые средства измерения (имитаторы) и поверяют рабочие средства измерений методом прямых измерений.

Для аттестации имитаторов (магазинов сопротивлений, индукционных катушек, пластов в контрольно-поверочных скважинах и т.д.) исполь­зуют скважинные средства измерений повышенной стабильности (стабиль­ность не менее 0.25 % за 0.5 ч), которые называют компараторами. С по­мощью компараторов передают размер единицы величины от исходных образцовых средств на имитаторы. Предел основной допустимой погрешно­сти образцовых средств измерения 1.5 — 2.5 %.

С помощью имитаторов аттестуют рабочие средства измерений на производственных геофизических предприятиях в ремонтно­поверочных лабораториях и цехах.

В электромагнитных методах каротажа измеряются параметры поля, которые связаны с электрическими свойствами горных пород. В об­щем случае каждый параметр поля зависит от s, р и ц среды. Поэтому электрические свойства среды находят из трансформаций, реализующих существующие теоретические представления. В этом случае, по- видимому, целесообразно иметь меры, которые позволили бы градуиро­вать аппаратуру в единицах параметров поля.

В некоторых случаях, когда возможно прямое измерение е и р, градуировать скважинные средства измерений можно непосредственно в единицах 8 и р.

Современная аппаратура индукционного каротажа поверяется пре­имущественно с помощью имитаторов р, выполненных в виде индукци­онной катушки, в цепь которой последовательно включаются резисторы и емкость для компенсации реактивной составляющей комплексного со­противления.

На рисунке приведена принципиальная схема имитатора для аппа­ратуры ИК, входящего в состав установки УПЭК-1.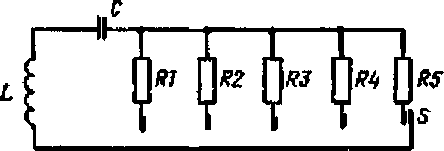







Индукционная катушка L выполнена на гетинаксовом каркасе и содержит 10 витков множительного медного провода (для повышения добротности и уменьшения скин-эффекта) со средним диаметром на­мотки 360 мм. В составе установки УПЭК имеется вторая катушка с диаметром намотки 700 мм. Емкость конденсатора С подбирается экс­периментально таким образом, чтобы на частотах 25 и 50 кГц индук­тивное сопротивление цепи равнялось емкостному сопротивлению. Со­противления резисторов Rl - R5 (магазины сопротивлений) определяют для каждого типа зонда аппаратуры ИК путем математического модели­рования электромагнитного поля в имитаторе и в бесконечной однород­ной среде. Резисторы Rl - R5 переключают при помощи переключателя. В аппаратуре АИК-5 имитации значений реактивной составляющей удельного электрического сопротивления (проводимости) производится из­менением емкости конденсатора С.

Поверку аппаратуры ИК выполняют в следующей последователь­ности [13]:

1. 
   зонд аппаратуры ИК располагают горизонтально на диэлектри­ческих подставках высотой не менее 1.5 м и размещают на нем вблизи генераторной катушки индукционную катушку имитатора;
   
2. 
   включают аппаратуру и по истечении времени ее самопрогрева выполняют калибровку по стандарт-сигналам в соответствии с техниче­ским описанием и инструкцией по эксплуатации;
   
3. 
   устанавливают на зонд вблизи генераторной катушки индукцион­ную катушку имитатора и, перемещая ее вдоль оси зонда, добиваются максимального сигнала на выходе поверяемой аппаратуры ИК;
   
4. 
   включают в цепь имитатора резистор (или магазин сопротивле­ний), значение сопротивления которого R_a соответствует началу диапа­зона измерений поверяемой аппаратуры и фиксируют результат изме­рений;
   
5. 
   измеряют поверяемой аппаратурой остальные значения, воспро­изводимые имитатором (в случае существенной случайной составляю­щей погрешности выполняют многократные измерения каждого значения);
   
6. 
   для каждого измеренного результата определяют оценку по­грешности аппаратуры.
   

Были предложены и другие способы поверки аппаратуры индук­ционного и электромагнитного каротажа.

В 1986 г. С.М. Аксельродом получено авторское свидетельство на способ поверки аппаратуры индукционного каротажа. Суть изобретения состоит в перемещении проводящего кольца вдоль катушечной системы зонда ИК для получения дифференциальной радиальной характери­стики зонда. По результатам сопоставления этой характеристики с рас­четной делают вывод о качестве аппаратуры [9].

В 1998 г. Западно-Сибирским НИИ геофизических методов развед­ки (изобретатели В.Н. Зосимов, И.Ф. Радковец, В.Г. Мамяшев) получен патент на способ градуировки аппаратуры индукционного каротажа. Способ включает в себя подачу на вход измерительного датчика сигна­лов от имитатора, проводимость которых меньше зоны чувствительно­сти прибора и чуть больше ее. После этого по показаниям прибора вы­числяется значение оь, которое затем служит «нулем воздуха» при проведении скважинных измерений.

Электрические свойства растворов электролитов

Электропроводность






■-Е

10"

(1.1)

ы щ
Согласно [22], электропроводность системы, состоящей из п заря­женных частиц, находящихся в хаотическом движении и между кото­рыми отсутствует взаимодействие (аналогично частицам идеального га­за), может быть описана выражением

где v₍ - число частиц i -го вида в одном кубическом метре, q_h т,- — заряд и масса г -й частицы, ц - время релаксации.

В общем случае величину г„ характеризующую интервал времени между двумя столкновениями частицы, определить сложно. Однако р можно выразить через длину свободного пробега / и скорость движения

Т

Vo частицы. Поэтому величина —, называемая подвижностью р [47],

m








т

м=—

1

m V₀m

Из кинетической теории газов [47] известно, что

-mV} =-кТ 2 ⁰ 2

тогда р

]К_

ЗкТ'

(1.2)

(1.3)

(1.4)
может быть описана следующим выражением:

здесь Т абсолютная температура, к — постоянная Больцмана.

IV

Произведение равно коэффициенту диффузии D движущихся

частиц. В то же время коэффициент диффузии равен [47]



(1.5)

D = -± 3
/К кТ

6 кщ

где г_г - радиус движущихся частиц (м), г] - коэффициент динамиче­ской вязкости.

Подстановка соотношений (1.4) и (1.5) в (1.1) дает для удельной электропроводности следующее выражение:

Соотношение (1.6) представляет известную формулу для удельной электропроводности электролитов. Оно справедливо лишь для очень слабых электролитов и обычно используется для определения эффек­тивных (стоксовских) радиусов частиц [52]. В этой области кулоновским взаимодействием можно пренебречь и движение частиц будет хаотич­ным, а их скорость будет определяться только температурой.

Увеличение содержания ионов в растворе приводит к увеличению влияния дальнодействующих сил кулоновского взаимодействия между частицами. Системы, состоящие из значительного числа заряженных частиц, характеризуются тем, что каждый отдельный ион находится в поле остальных ионов, но система в целом остается электронейтраль­ной. Последнее приводит к тому, что в растворе для системы ионов ус­танавливается определенная регулярная структура. В то же время те­пловое движение частиц стремится нарушить эту структуру. Это при­водит к непрерывной флюктуации полей как по величине, так и по на­правлению. В реальных системах, на движения ионов влияют не только температура, но и поля, создаваемого зарядами. Вследствие этого и значения времени релаксации г_; будет изменяться.

Следовательно, тепловая энергия будет расходоваться не только на движение частиц, но и на преодоление энергии кулоновского поля U_k

(1.7)

Из (1.2) - (1.6), с учетом (1.7) получается для удельной электропро­водности следующее выражение:



(1.8)
f кя-ит

^₂ блщ(ЗкТ-2U_k)

В основе этого способа расчета удельной электропроводности силь­ных электролитов лежит предположение, о том, что ионы не движутся, а лишь хаотически колеблются около своих положений равновесия. Т. е. в растворах существует не только определенная структура растворите­ля [40], но и структура растворенного вещества. В концентрированных растворах последняя может быть подобна кристаллической структуре. Таким образом, при расчете энергии кулоновского взаимодействия можно использовать метод расчета энергии кристаллической решетки по Борну [39]



(1.9)

и_к=-
Ыг^А

Алеева ^ s )

где <7, - заряды ионов, s - относительная диэлектрическая прони­







трами ионов, А - структурная постоянная,

'i-Г

V

SJ

множитель, учиты­
цаемость, £q - диэлектрическая постоянная, а - расстояние между цен­

вающий энергию отталкивания.

В слабоконцентрированных растворах расстояния между ионами значительно больше, чем в кристаллах, и поэтому силы отталкивания можно не учитывать. Однако при концентрациях электролитов больше 1 Моль/литр эти расстояния становятся одного порядка и необходимо учитывать силы отталкивания.

Расчет удельной электропроводности растворов NaCl по формулам (1.8) - (1.9) показал их хорошее совпадение со справочными данными [10, 44]. Поэтому они в дальнейшем используются для расчетов УЭС растворов электролитов с учетом температуры и концентрации.

Практически важной является оценка частотной дисперсии элек­тропроводности растворов электролитов. Из работ [26, 45, 49] следует, что она обусловлена в первую очередь дисперсией дипольной электро­проводности воды и составляет пренебрежимо малую величину (поряд­ка ЗЮ^-7 См/см) при рассматриваемых нами частотах (порядка 10⁶­10⁷ Гц) и концентрациях (1 Моль/литр). Поэтому, при дальнейшем рас­смотрении этим эффектом можно пренебречь.

Диэлектрическая проницаемость

Анализ литературы [45, 49] показал, что в настоящее время нет общей точки зрения на величину диэлектрической проницаемости рас­твора той или иной соли. По мнению одних авторов диэлектрическая проницаемость бинарного раствора электролита увеличивается с ростом концентрации, по мнению других - уменьшается, или, в зависимости от состава солей, возрастает или уменьшается. Тем не менее, в большин­стве случаев эти изменения малы и в первом приближении могут быть рассчитаны по формуле (1.10) Г. Фалькенгагена [46]. При этом предпо­лагается, что с ростом концентрации солей диэлектрическая проницае­мость растворов должна увеличиваться.

£*=^+3.7971 (1.10)

где е - диэлектрическая проницаемость раствора;

£*₀- диэлектрическая проницаемость дистиллированной воды;

Л - концентрация раствора, Моль/литр.

Большинство исследователей сходится на том, что с увеличением температуры раствора его диэлектрическая проницаемость уменьшает­ся. Это подтверждается и экспериментальными данными для водного раствора NaCl [10].

т° с	Концентрация, Моль/литр
	0.125	0.333	0.66	1.00	2.08	4.34	5.62
3	85.8	81.9	77.2	74.0	-	-	-
25	78.0	73.0	68.7	65.0	52.2	37.6	32.1
40	71.5	69.7	67.1	64.3	-	-	-

Таким образом, можно сделать следующие выводы: с увеличением минерализации диэлектрическая проницаемость би­нарных растворов в сравнении с диэлектрической проницаемостью дистиллированной воды изменяется незначительно; с увеличением температуры диэлектрическая проницаемость бинар­ных растворов существенно уменьшается.

Следовательно, в случае применения в метрологических моделях, диэлектрические свойства растворов можно считать независящими от концентрации соли, а учет температурных зависимостей необходим на­ряду с учетом температуры для электропроводности. Для этого необхо­димо проводить тщательные измерения температуры до и после прове­дения работ.

1.3 Электромагнитное поле магнитного диполя

Уравнения Максвелла для квазистационарного поля:

rotЁ = -—\ div7 = 0
dt

rotН = aj ; divB = 0

где о - удельная электропроводность среды.

Уравнения связи j = аЁ, В = pH.

Будем предполагать, что размеры генераторной катушки сущест­венно меньше расстояния до точки измерения. В этом случае круглый виток с переменным током I(t) = 1₀е^ш, можно заменить на диполь с из­меняющимся во времени моментом: М = М₀е^ш, (О - циклическая часто­та.

В однородной среде

Введем цилиндрическую систему координат \r, <р, z). Ось z направ­лена вдоль момента диполя. Начало координат расположено в источни­ке. Введем вектор-потенциал А, связанный с электромагнитным полем следующими соотношениями:

Е = ico/u rot А Н = k² А + grad div А

где: к¹ - -тар

В силу симметрии задачи существует всего три ненулевые компо­ненты поля

Компонента потенциала подчиняется уравнению Гельмгольца

V²A_z + k²A_z = О, при R*0

Как известно, решение этого уравнения имеет вид

где R = ylr² +z² ,

тогда из (1.1) следует, что


4 nR
E_r=i_m-^e“\\ + kR)

H_z=-^-_Te-^kR(l-kR) ^z In R^{3 V} '

При условии квазистационарности волновое число к преобразуется к виду

здесь f=co/2n частота в МГц.

При этом разность фаз между э.д.с в приемных катушках

5L- —, L - длина наибольшего зонда

В присутствии тонкой проводящей пластины

В случае, когда электропроводность слоя во много раз превышает электропроводность окружающей среды, а толщина слоя во много раз меньше длины зонда, то можно пренебречь распространением поля внутри слоя можно говорить о продольной проводимости слоя s = a-h, где а со - электропроводность слоя, h -» 0 - толщина слоя.

Граничные условия для вертикальной компоненты А_г следуют из непрерывности тангенциальных компонент поля

4 = 4 L ^; IT Г ^{= ia)}v^sA2

¹ dz dz










Д =

\_ 4 л

V

/I

-i|,|

Ак²е^2Щ

А," МЧ+kt)

е²^ \J₀(Ar)dA;
Тогда для вектор-потенциала имеем:



e^J^Ar)dA

Д
2А

4л *2A_l+k_s где k² = -icojus.








_Я1 _=Ho₊!®i^usz Г ^те

3 -т(1+2^)

00 3 -ГП\

m е ¹

2т_х - ico/usz

2 ' т_х (2т_[ kopsz)

dm,

dm;
Для вертикальной компоненты магнитного поля на оси диполя, со­гласно (1.2):

где т- Az, m_l= sjm² -k²z² .

В цилиндрически-слоистой среде

При переходе через поверхность раздела г = а₁ тангенциальные

компоненты электрического и магнитного поля меняются непрерывно.

Для этого необходимо











^z² '

к² А\ + = к₂А₂ + -

dz

Тогда решение на оси среды имеет вид