МАТ.+АНАЛИЗ+22+ИВО (4). Литература Шипачев В. С. Высшая математика, учебник, Москва Изд во Юрайт, 2015 г. Второй семестр
 Скачать 79.23 Kb. Скачать 79.23 Kb.
|
|
Математический анализ Литература Шипачев В.С. Высшая математика, учебник, Москва: Изд –во Юрайт, 2015 г. ВТОРОЙ СЕМЕСТР. Модуль 2. Анализ функций многих переменных. Модульная единица 7. Дифференциальное исчисление функции многих переменных. Модульная единица 8. Кратные интегралы. Модуль 3. Ряды. Дифференциальные уравнения. Модульная единица 9. Ряды. Модульная единица 10. Дифференциальные уравнения первого порядка. Модульная единица 11. Дифференциальные уравнения второго порядка. ВТОРОЙ СЕМЕСТР. Модуль 2. Анализ функции многих переменных. Модульная единица 8. Кратные интегралы. Лекция 5. Двойной интеграл. Пусть задана непрерывная функция двух переменных 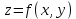 , определенная в некоторой области , определенная в некоторой области  Например, функция Например, функция 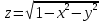 определена в области, заданной неравенством определена в области, заданной неравенством 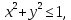 то есть в круге с центром в начале координат и с радиусом единица. Нетрудно видеть, что эту функцию можно также задать в виде то есть в круге с центром в начале координат и с радиусом единица. Нетрудно видеть, что эту функцию можно также задать в виде  то есть это то есть это  уравнение положительной полусферы с радиусом, равным единице. уравнение положительной полусферы с радиусом, равным единице.Разобьем область  вертикальными и горизонтальными прямыми на множество частей вертикальными и горизонтальными прямыми на множество частей 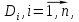 и обозначим их площади через и обозначим их площади через 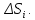 Внутри каждой части Внутри каждой части  возьмем точку возьмем точку  и подсчитаем значение функции и подсчитаем значение функции 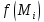 в этой точке (рис.1). Тогда произведение в этой точке (рис.1). Тогда произведение  будет обозначать объем цилиндрического тела с площадью основания будет обозначать объем цилиндрического тела с площадью основания  и высотой и высотой  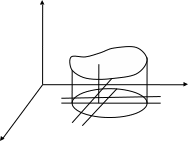 Рис.1. Геометрический смысл двойного интеграла  объем цилиндрического тела. объем цилиндрического тела.Выражение  = =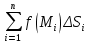 называется интегральной суммой функции называется интегральной суммой функции 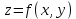 в области в области  Определение 1. Предел интегральной суммы при стремлении всех 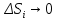 (то есть при (то есть при 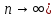 называется двойным интегралом от функции называется двойным интегралом от функции 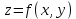 по области по области  и обозначается и обозначается (1) (1) Свойства двойного интеграла. Если функция 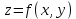 непрерывна в замкнутой ограниченной области непрерывна в замкнутой ограниченной области  то она интегрируема в этой области, то есть существует двойной интеграл (1). то она интегрируема в этой области, то есть существует двойной интеграл (1).Постоянное число выносится за знак интеграла:  (2) (2)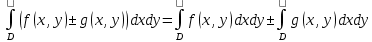 (3) (3) то то 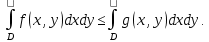 (4) (4)Если  причем причем 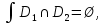 то то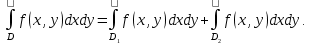 (5) (5)(Теорема о среднем значении). Если функция 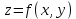 непрерывна в замкнутой ограниченной области непрерывна в замкнутой ограниченной области  то найдется такая точка то найдется такая точка  что что 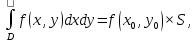 (6) (6)где  площадь области площадь области  (Объем обычного цилиндра высотой (Объем обычного цилиндра высотой  равен объему цилиндра с криволинейной поверхностью равен объему цилиндра с криволинейной поверхностью  Вычисление двойного интеграла. Теорема. Пусть функция  определена и непрерывна в замкнутой ограниченной области определена и непрерывна в замкнутой ограниченной области  , задаваемой неравенствами: , задаваемой неравенствами: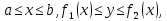 (7) (7)и для каждого  существует интеграл существует интеграл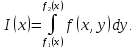 Тогда Тогда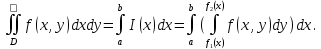 (8) (8)Для удобства последнее равенство записывают в виде: 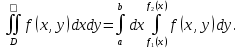 (9) (9)Иногда вычисление двойного интеграла более удобно выполнять в другом порядке, сначала по 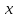 , а потом по , а потом по 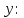 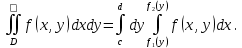 (10) (10) Замена переменных в двойном интеграле. При переходе от переменных 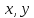 к новым переменным к новым переменным 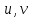 используется формула используется формула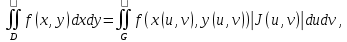 (11) (11)где 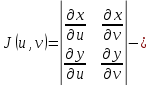 определитель Якоби (якобиан), а определитель Якоби (якобиан), а  область в плоскости область в плоскости  , в которую переходит область , в которую переходит область  Пример 1. Вычислить интеграл 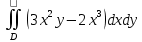 , где область , где область  задана: задана: 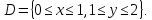 Решение. 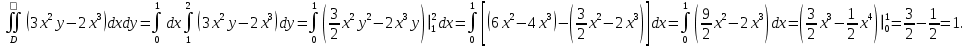 Пример 2. Вычислить интеграл  , где область , где область  задана: задана: 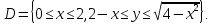 (см. рис. 2). (см. рис. 2). Рис.2.  Решение. 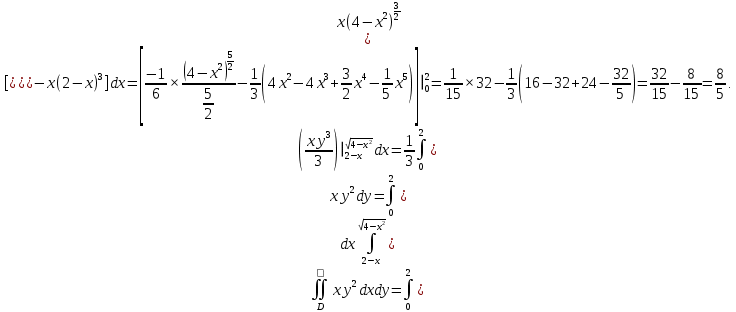 Пример 3. Вычислить интеграл  , где область , где область  задана: задана:  Рис. 3. Область  ограниченная осью ограниченная осью  и прямыми и прямыми  Решение 1. 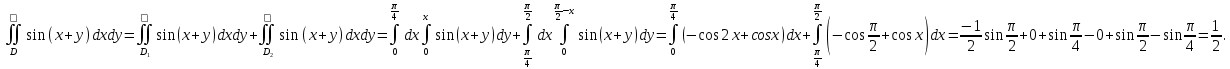 Решение 2 (по формуле (10)). 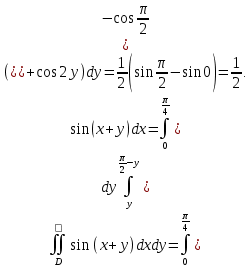 Пример 4. Вычислить интеграл 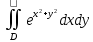 по области по области 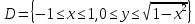 (рис. 4). (рис. 4). Рис.4. Переход к полярной системе координат.  Перейдем к полярной системе координат 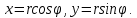 При этом область При этом область  перейдет в область перейдет в область 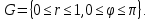 Подсчитаем определитель Якоби:  Применяя формулу (11), получим  Задания для самостоятельной работы Вычислить интеграл 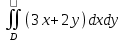 , где область , где область  задана: задана: 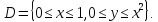 Вычислить интеграл 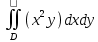 , где область , где область  задана: задана:  Вычислить интеграл 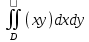 , где область , где область  задана: задана: 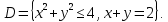 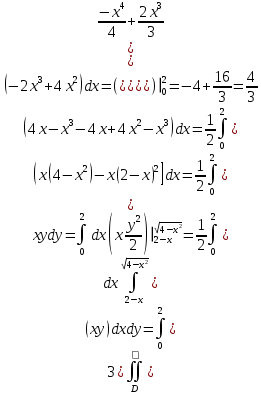 . . Вычислить интеграл  , где область , где область  задана: задана: 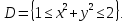  Лекция 6. Тройной интеграл Понятие тройного интеграла возникло из практических потребностей вычисления массы объемного тела с переменной плотностью, количества тепла, содержащегося в заданном объеме, и т. д . Если разбить объемную область  на множество частей на множество частей  , взять внутри каждой части точку , взять внутри каждой части точку(  и вычислить все значения и вычислить все значения 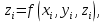 то масса (количество тепла) данного тела будет приблизительно равна так называемой интегральной сумме то масса (количество тепла) данного тела будет приблизительно равна так называемой интегральной сумме (1) (1)где  объемы частей объемы частей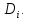 Определение 1. Тройным интегралом от функции  называется предел интегральной суммы (1) при называется предел интегральной суммы (1) при 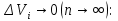 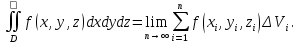 (2) (2) Свойства тройного интеграла.   Если  причем причем  то то  ( Теорема о среднем значении). Если функция  непрерывна, то найдется такая точка непрерывна, то найдется такая точка 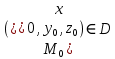 , что , что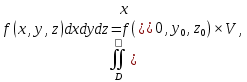 где где  объем области объем области  Вычисление тройного интеграла. Теорема. Пусть функция  определена и непрерывна в области определена и непрерывна в области  Тогда: Тогда: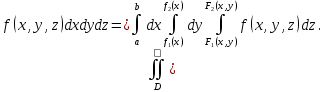 В частности, если требуется вычислить тройной интеграл от функции  по прямоугольному параллелепипеду по прямоугольному параллелепипеду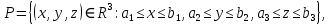 то то 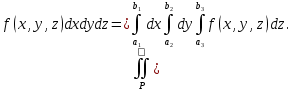 Цилиндрические и сферические координаты. Замена переменных в тройном интеграле. Довольно часто вычисление тройного интеграла более удобно произвести не в прямоугольной системе координат, а в цилиндрической, либо в сферической системе координат. Итак, что такое цилиндрическая система координат? Это – полярная система координат 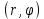 в плоскости в плоскости  , плюс ось , плюс ось 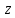 (см. рис. 1): (см. рис. 1): 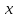 Рис.1.Цилиндрическая система координат 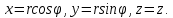 (3) (3)Теперь опишем сферическую систему координат. Пусть точка 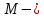 некоторая точка трехмерного пространства. Ее положение можно задать с помощью трех величин (см. рис. 2): длиной ρ вектора некоторая точка трехмерного пространства. Ее положение можно задать с помощью трех величин (см. рис. 2): длиной ρ вектора 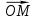 с началом в точке с началом в точке 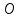 и окончанием в точке и окончанием в точке 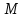 , углом 𝜑, отсчитываемом от оси , углом 𝜑, отсчитываемом от оси  до проекции вектора до проекции вектора 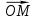 на плоскость на плоскость  , а также углом , а также углом  , отсчитываемом от оси , отсчитываемом от оси 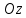 до вектора до вектора 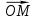 . . 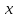 Рис. 2. Сферическая система координат. Нетрудно установить соотношения между прямоугольной системой координат и сферической системой координат:  (4) (4)В общем случае, при переходе от координат 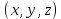 к другим координатам к другим координатам  по формулам по формулам (5) (5)тройной интеграл принимает вид: 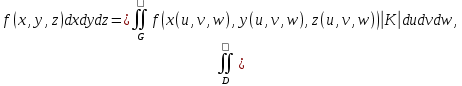 где область 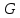 является ОБРАЗОМ области является ОБРАЗОМ области  в результате преобразования, определяемого формулами (5), а в результате преобразования, определяемого формулами (5), а 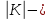 «коэффициент сжатия» элементарного объема «коэффициент сжатия» элементарного объема  к элементарному объему к элементарному объему  при переходе к координатам  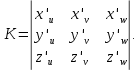 (6) (6)При переходе к цилиндрической системе координат 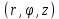 (3), получим: (3), получим: При переходе к сферической системе координат  (5), получим: (5), получим: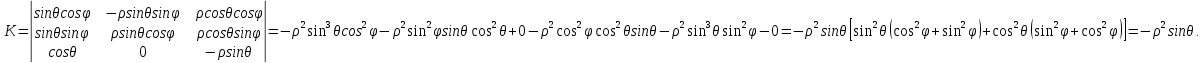 Пример 1. Вычислить интеграл  , где область , где область  представляет собой тетраэдр, ограниченный плоскостями представляет собой тетраэдр, ограниченный плоскостями 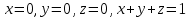 (см. рис. 3): (см. рис. 3):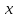 Рис. 3. Тетраэдр. Нетрудно видеть, что в плоскости 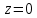 если если 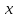 изменяется от нуля до единицы, то изменяется от нуля до единицы, то 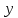 изменяется от нуля до изменяется от нуля до 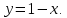 Далее, для любой точки Далее, для любой точки 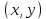 в треугольнике в треугольнике 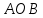 компонента компонента 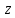 будет изменяться от нуля до будет изменяться от нуля до 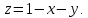 Поэтому Поэтому . . Пример 2. Вычислить интеграл  , где область представляет собой верхнюю половину эллипсоида , где область представляет собой верхнюю половину эллипсоида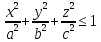 (см. рис. 4): (см. рис. 4):    Рис. 4. Верхняя половина эллипсоида. Нетрудно видеть, что в плоскости 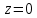 если если 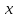 изменяется от изменяется от 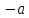 до до  , то , то 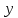 изменяется от изменяется от 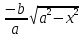 до до   Далее, для любой точки Далее, для любой точки 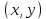 внутри эллипса компонента внутри эллипса компонента 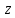 будет изменяться от нуля до будет изменяться от нуля до 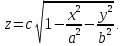 Поэтому Поэтому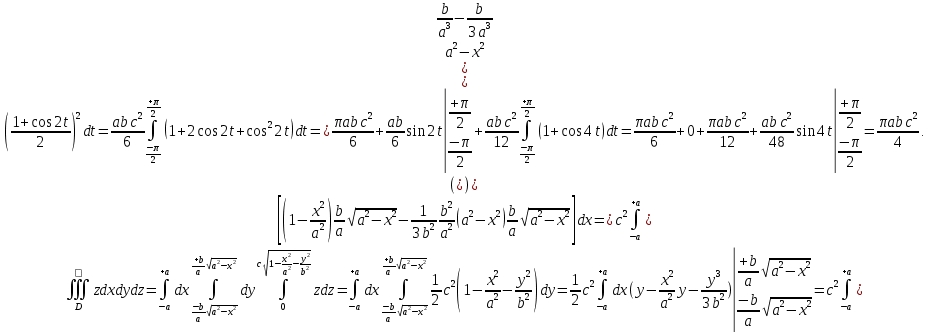 (  Пример 3. Вычислить интеграл  , где область , где область  представляет собой часть конуса, ограниченного поверхностью представляет собой часть конуса, ограниченного поверхностью 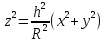 и плоскостью и плоскостью 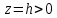 (см. рис. 4): (см. рис. 4):  Рис. 5. Конус высотой 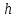 с вершиной в начале координат. с вершиной в начале координат.Нетрудно видеть, что в плоскости 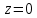 если если 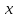 изменяется от изменяется от  до до  , то , то 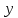 изменяется от изменяется от 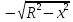 до до   Далее, для любой точки Далее, для любой точки 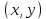 внутри круга внутри круга 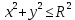 компонента компонента 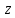 будет изменяться от будет изменяться от 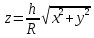 до до 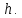 Поэтому Поэтому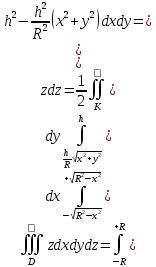 , , (  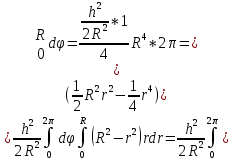 Задания для самостоятельной работы. Вычислить интеграл  , где область , где область  ограничена поверхностями ограничена поверхностями 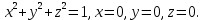 Перейдя к цилиндрическим координатам, вычислить интеграл 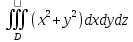 , где область , где область  ограничена поверхностями ограничена поверхностями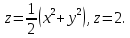 Модуль 3. Ряды. Дифференциальные уравнения. Модульная единица 9. Ряды. Лекция 7. Числовые ряды. Сумма элементов бесконечной числовой последовательности 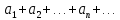 или или (1) (1)называется числовым рядом. Сумма конечного числа элементов числовой последовательности 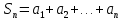 называется ЧАСТИЧНОЙ СУММОЙ ряда. называется ЧАСТИЧНОЙ СУММОЙ ряда.Определение 1. Если существует КОНЕЧНЫЙ предел последовательности частичных сумм 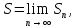 то ряд (1) называется СХОДЯЩИМСЯ, а число то ряд (1) называется СХОДЯЩИМСЯ, а число  СУММОЙ ряда. В противном случае ряд (1) называется РАСХОДЯЩИМСЯ. СУММОЙ ряда. В противном случае ряд (1) называется РАСХОДЯЩИМСЯ.Простейшим примером сходящегося ряда является сумма элементов так называемой бесконечно убывающей прогрессии:  (2) (2)при условии, что  . . Действительно, запишем два равенства для частичной суммы этого ряда: 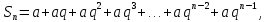  Вычитая из первого равенства второе, получим: 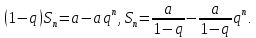 Поскольку, как известно, 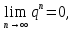 при при  то то 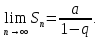 Примером расходящегося ряда является сумма элементов так называемого ГАРМОНИЧЕСКОГО ряда:  (3) (3)Рассмотрим следующую последовательность частичных сумм ряда (3) 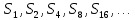 Можно убедиться в том, что каждая следующая частичная сумма больше предыдущей как минимум на  А это значит, что предел этой последовательности равен бесконечности! А это значит, что предел этой последовательности равен бесконечности! Действительно, 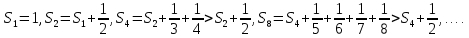 Приведем еще один пример сходящегося ряда: 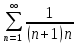 (4) (4)Возьмем частичную сумму и вычислим ее: 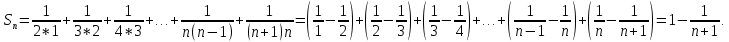 В результате легко получаем, что 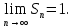 Теорема 1. (Необходимое условие сходимости ряда). Если ряд (1) сходится, то 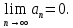 Действительно, так как ряд (1) сходится, то 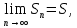 а также а также 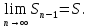 Отсюда следует, что Отсюда следует, что Теорема 2. Исходный ряд  и ряд и ряд 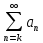 (то есть, начиная не с первого, а с (то есть, начиная не с первого, а с  того элемента) вместе сходятся или расходятся. того элемента) вместе сходятся или расходятся.Знакоположительные ряды. Далее рассмотрим условия сходимости и расходимости рядов с неотрицательными элементами, то есть когда все 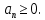 Теорема 3. Пусть даны два ряда 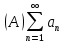 и и 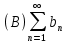 , ,причем, начиная с некоторого номера имеет место неравенство 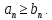 Тогда из сходимости ряда 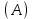 следует сходимость ряда следует сходимость ряда 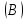 , и наоборот, если расходится ряд , и наоборот, если расходится ряд  , то расходится и ряд , то расходится и ряд 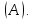 В силу теоремы 2, мы можем без ограничения общности считать, что  выполняется с первого номера. выполняется с первого номера.Далее, для частичных сумм  ряда ряда 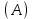 и и 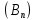 ряда ряда  выполняется неравенство выполняется неравенство 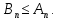 Поскольку ряды знакоположительные, то последовательности частичных сумм Поскольку ряды знакоположительные, то последовательности частичных сумм  и и  монотонно возрастающие. Кроме того, нам дано, что ряд монотонно возрастающие. Кроме того, нам дано, что ряд 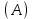 сходится, то есть существует сходится, то есть существует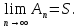 Это значит, что для всех Это значит, что для всех 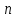 имеет место неравенство имеет место неравенство 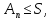 а поэтому и а поэтому и  Но последовательнось монотонно возрастающая и ограниченная сверху всегда имеет предел, то есть ряд Но последовательнось монотонно возрастающая и ограниченная сверху всегда имеет предел, то есть ряд  тоже сходится. тоже сходится.Вторая часть теоремы следует из первой части (доказательство от противного). Для практического применения более удобной является Теорема 4. Если существует предел  то оба ряда вместе сходятся или расходятся. Если 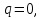 то из сходимости ряда то из сходимости ряда  следует сходимость ряда следует сходимость ряда 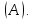 Если Если 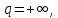 то из сходимости ряда то из сходимости ряда 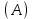 следует сходимость ряда следует сходимость ряда  Примеры. Ряд 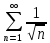 расходится, так как при всех расходится, так как при всех 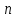 имеет место неравенство имеет место неравенство 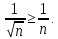 Ряд  сходится, так как при всех сходится, так как при всех 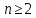 имеет место неравенство имеет место неравенство 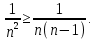 ( (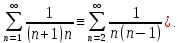 Теорема 5. (Признак сходимости Даламбера). Пусть существует предел 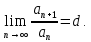 Тогда, если Тогда, если 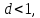 то ряд то ряд  сходится, если сходится, если 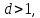 то ряд то ряд  расходится. ( В случае, когда расходится. ( В случае, когда 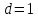 ответ неясен). ответ неясен).Примеры. 1) Ряд 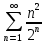 сходится, так как сходится, так как  2)Ряд 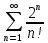 сходится, так как сходится, так как 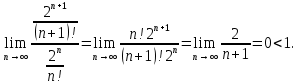 Теорема 6. (Признак сходимости Коши). Пусть существует предел  Тогда, если Тогда, если  то ряд то ряд  сходится, если сходится, если  то ряд то ряд  расходится. ( В случае, когда расходится. ( В случае, когда  ответ неясен). ответ неясен).Примеры. 1) Ряд  сходится, так как сходится, так как 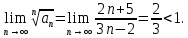 2)Ряд 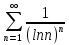 сходится, так как сходится, так как  Задания для самостоятельной работы. Доказать сходимость ряда и найти его сумму. 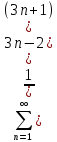 . .2. Исследовать сходимость знакоположительных рядов. a) 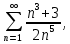 b)  c)  3.Исследовать сходимость знакоположительных рядов. 1) 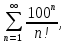 2)  3) 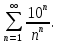 |
