ҮСЗ. лкен сандар задары. Чебышев теоремасы. Бернулли теоремасы Бернулли теоремасы
 Скачать 19.47 Kb.
|
|
Үлкен сандар заңдары. Чебышев теоремасы. Бернулли теоремасы Бернулли теоремасы Тәжірибені шексіз көп жүргізгенде оқиғаның пайда болу жиілігі оның ықтималдығынан тым аз айырмашылықта болатындығын атап өткенбіз. Міне бұл "үлкен сандар заңының" бір көрінісі. Үлкен сандар заңы деп кездейсоқ шамалардың арифметикалық ортасына тұжырымдалатын теоремаларды айтамыз. Чебышев теоремасы. Егер тәуелсіз Х 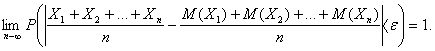 , Х ,..., Хn кездейсоқ шамаларының тұрақты бір С санымен шектелген дисперсиялары бар болса, онда кез-келген ε>0 саны үшін Яғни, кездейсоқ шамалардың арифметикалық ортасы мен олардың математикалық үміттерінің арифметикалық ортасының арасындағы айырмашылық кездейсоқ шамалар саны мейлінше көп болғанда (n  ) өте аз шама болады.Чебышев теоремасы чебышев теңсіздігі арқылы дәлелденеді. Бұл айтылғанның практикалық маңызын әрі қарай түсіну үшін үлкен сандар заңының тағы басқа теоремасын қарастырайық. Бернулли теоремасы. Егер Р әрбір тәжірибе жүргізгендегі А оқиғасының пайда болу ықтималдығы және кездейсоқ шамасы – А оқиғасының n рет тәжірибе жүргізгендегі пайда болу саны m болса, онда кез келген ε >0 саны үшін  Бернулли теоремасы тәжірибе жүргізу шарты тұрақты болғанда жиіліктің орнықты болуын көрсетеді. |