Логические данные и выражения. Операторы разветвления vс. Программная реализация базовых разветвляющиеся структур и типовых алгоритмов студент гр. Бик2104 Косых А. В
 Скачать 348.68 Kb. Скачать 348.68 Kb.
|
|
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Кафедра «Информатика» Лабораторная работа №7-1 ««Разработка проекта, решающего задачу принадлежности или непринадлежности точки с заданными координатами геометрической фигуре» по теме «Логические данные и выражения. Операторы разветвления VС++. Программная реализация базовых разветвляющиеся структур и типовых алгоритмов» Выполнил: студент гр. БИК2104 Косых А.В. Вариант №15 Проверил: Воробейчиков Л.А. 1)Постановка задачи.  2)Формализация задания. Построенная вручную описанная в постановке задачи фигура представлена на рис.1 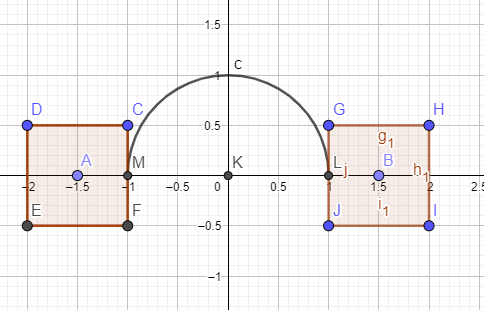 Рис.1-Фигура”Дедушкины очки” Для того,чтобы понять,попадет ли заданная точка в нужную нам область квадратов, следует ограничить координаты х и у следующим образом: В левом квадрате одновременно должны выполняться условия -2<=x<=-1 и -0,5<=y<=0,5 В правом квадрате одновременно должны выполняться условия 1<=x<=2 и -0,5<=y<=0,5 3) Следует учитывать и дугу: Уравнение этой полуокружности x^2+y^2=1,y>0 В виде выражения данные уравнения будут выглядеть так: ( ( y>=-0,5 && y<=0,5 ) && ( (x<=-1 && x>=-2) | | (x<=2 && x>=1) ) ) || ((y >= 0) && (pow(x, 2) + pow(y, 2) == 1)) Разработка схемы алгоритмов Схема алгоритма Resh1 представлена на рис.2. На ней изображено стандартное разветвление и сложное логическое выражение. 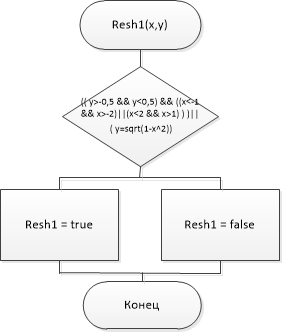 Рис.2- Схема алгоритма Resh1 Схема алгоритма Resh2 представлена на рис.3. На ней изображены вложенные разветвления только с помощью операций отношения, без использования логических операций и сложных логических выражений. 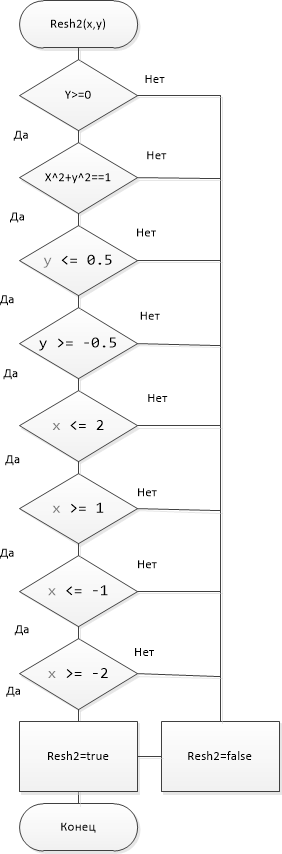 Рис.3-Схема алгоритма Resh2 Рис.3-Схема алгоритма Resh2 ( ( y>=-0,5 && y<=0,5 ) && ( (x<=-1 && x>=-2) | | (x<=2 && x>=1) ) ) || ((y >= 0) && (pow(x, 2) + pow(y, 2) == 1)) Полученное вами выражение представляет собой дизъюнкцию трёх конъюнкций, а схема алгоритма на рис.3 реализует конъюнкцию восьми условий. Схема алгоритма Resh3, использующая только сложное логические выражения,представлена на рис.4. 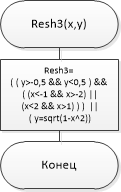 Рис.4-Схема функционального алгоритма Resh3, использующая только сложное логическое выражение. 4)Разработка программного кода. Программный код представлен на рис.5
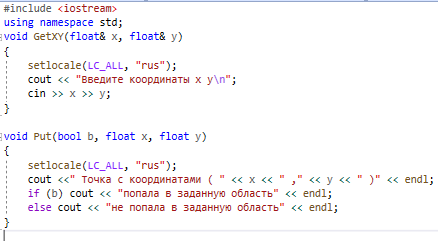
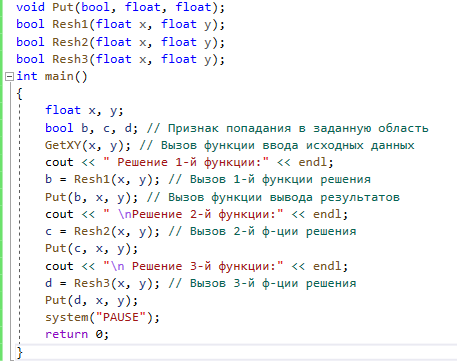
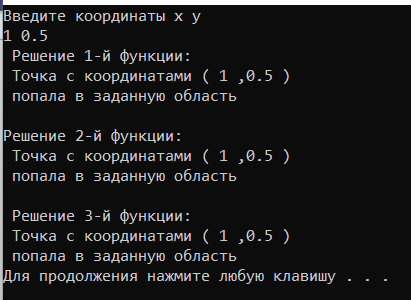
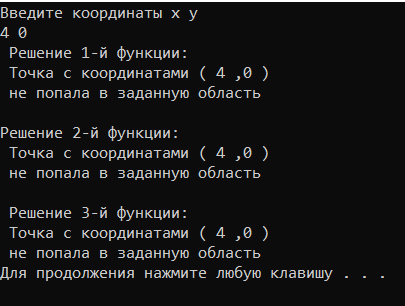
 Рис.5-Программный код проекта. Код функции Resh2 не соответствует схеме алгоритма на рис.3, и это плохо. Но он правильно решает задачу, и это хорошо. 5) Результаты программы. Получены результаты выполнения проекта, приведенные на рисунке 6, для тестовых данных точек, попадающих и не попадающих в заданную область.
Рис.6-Результаты работы программы 6)Доказательство правильности выполнения программы. 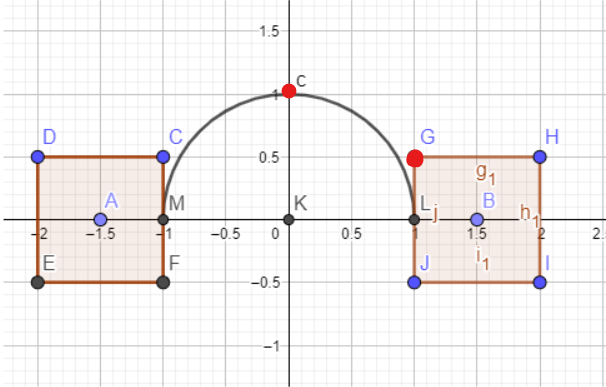 Программа работает верно. |