Логические величины, операции, выражения. Построение логических схем

• Название: Логические величины, операции, выражения. Построение логических схем
• Дата: 20.12.2022
• Размер: 236.62 Kb.
• Имя файла: №9.docx
• Тип: Практическая работа; #853943

Практическая работа №5,6

Тема: Логические величины, операции, выражения. Построение логических схем.

Цель работы: научиться составлять аналитические выражения по табличному значению функции, строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.

Студент должен

знать:

• 
  основной базис логики;
  
• 
  особенности применения логических элементов;
  

уметь:

• 
  производить синтез и анализ аналитических выражений логических функций
  
• 
  строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.
  

Теоретическое обоснование.

1. Логические элементы

Функция отрицание НЕ или инверсия

Таблица истинности функции отрицания имеет вид: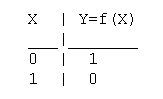



Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)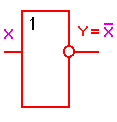

Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2

Таблица истинности логического ИЛИ имеет вид: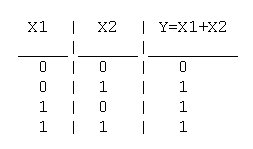



Логический элемент ИЛИ обозначается на схемах следующим образом: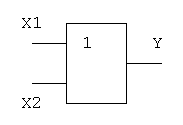

Логическое И (логическое умножение, конъюнкция): Y = X1X2 = X1&X2

Таблица истинности логического И имеет вид: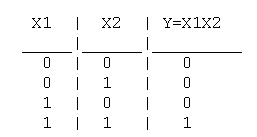



Логический элемент И обозначается на схемах следующим образом: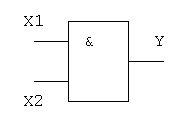

Функция ИЛИ-НЕ: Y = (X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид: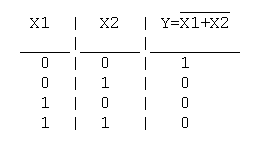



Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом: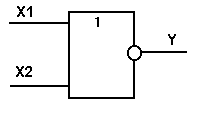

Функция И-НЕ: Y = (X1^X2)

Таблица истинности функции И-НЕ имеет вид: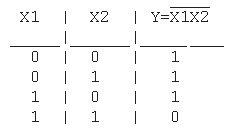



Логический элемент И-НЕ обозначается на схемах следующим образом: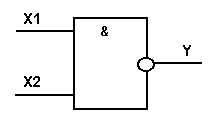

2. Алгоритм построение логических схем.

1. 
   Определить число логических переменных.
   
2. 
   Определить количество базовых логических операций и их порядок.
   
3. 
   Изобразить для каждой логической операции соответствующий ей вентиль.
   
4. 
   Соединить вентили в порядке выполнения логических операций.
   

Пример 1.
Составить логическую схему для логического выражения: F=A v B & A.
Две переменные – А и В.
Две логические операции: 1-&, 2-v.
Строим схему: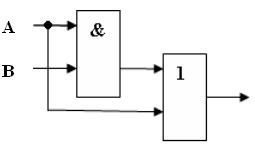


Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0.
Переменных две: А и В;
Логических операций три: & и две v; А&Вv (Вv А).
Схему строим слева направо в соответствии с порядком логических операций: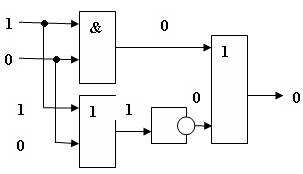


3. Составление аналитического выражения функции и построение логической схемы по табличному заданию функции.

Синтез комбинационных устройств может быть произведен по табличному заданию функции по «0» и «1». Рассмотрим для примера синтез по «1». Для всех значений аргументов х₁, х₂, х₃, где функция задана как «1» берется их конъюнкция, если аргумент равен «1», если же 0 – конъюнкция их инверсий. От полученных конъюнкций берется дизъюнкция.

Например, функция от трех аргументов задана следующей таблицей:

	х1	х2	Х3	у
1	0	0	0	0
2	0	0	1	1
3	0	1	0	0
4	0	1	1	0
5	1	0	0	0
6	1	0	1	0
7	1	1	0	0
8	1	1	1	1

Это значит, что при любых наборах аргументов ч кроме второго и последнего, аргумент у будет равен 0. Составляем для второго набора выражение: .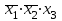

Для последнего набора: х₁ х₂ х₃

Составим аналитическое выражение функции: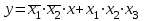


Схема должна содержать инверсию сигналов х₁, х₂, две схемы «И» и одну двухвходовую схему «ИЛИ»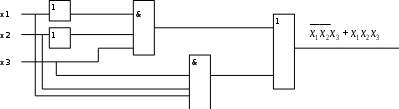



Ход работы:

1. 
   Изучить теоретическое обоснование;
   
2. 
   Выполнить практическое задание по вариантам;
   
3. 
   Оформить отчет.
   
4. 
   Ответить на контрольные вопросы по указанию преподавателя.
   

Практические задания:

Задание 1
Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.

Вариант 1

а)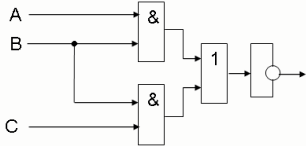


б)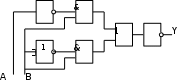

Вариант 2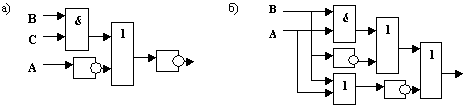



Вариант 3

а)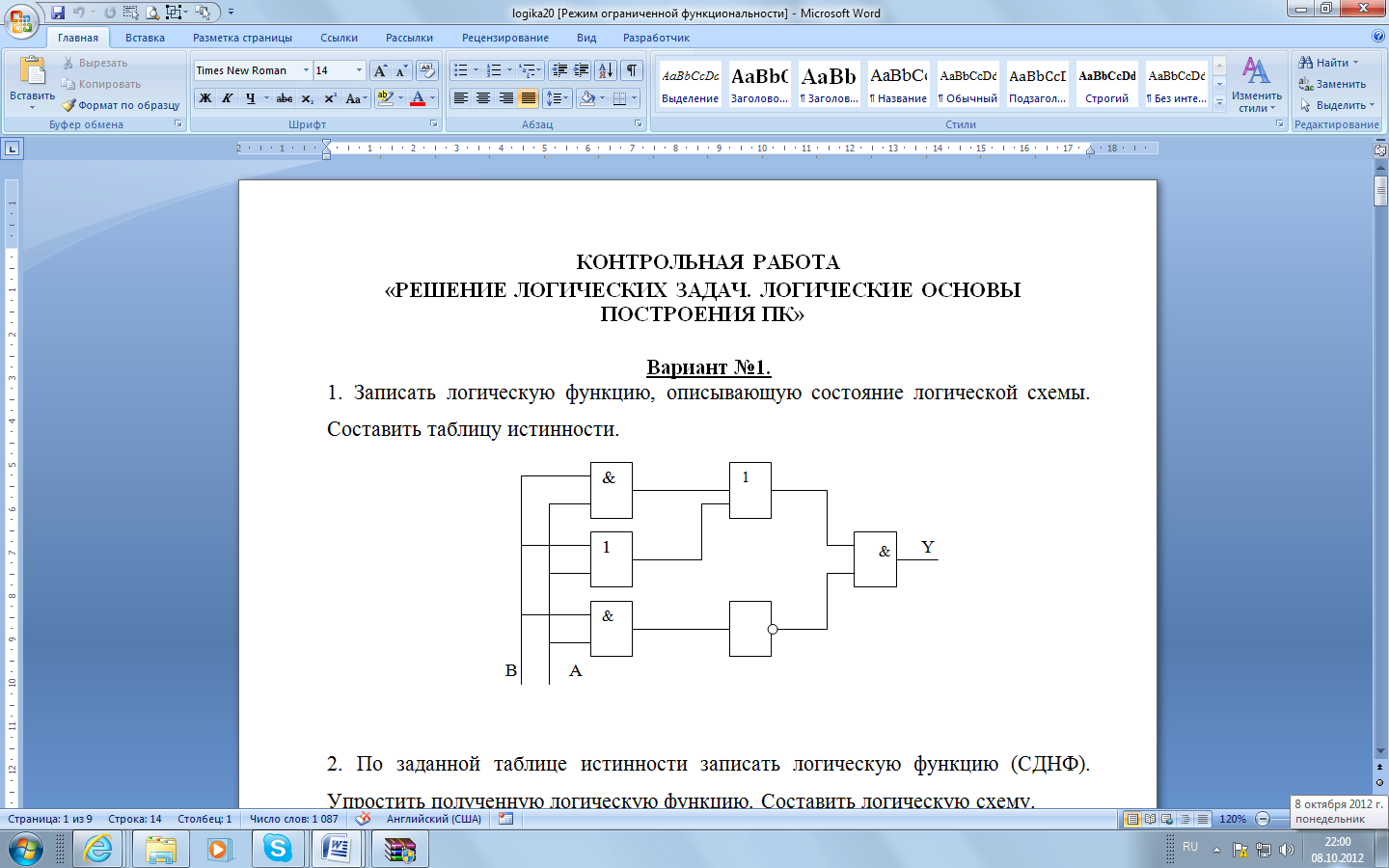



б)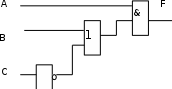

Вариант 4

а)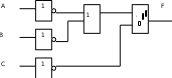


&


б)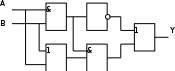

Задание 2

Построить логические схемы по формулам и составить таблицу истинности

Вариант 1

а) F= (AvB)&(Cv`B)

б) F= (A&B&C)

Вариант 2

а) F=(X&`Y)vZ.

б) F=X&Yv`Z.

В ариант 3
а)F= (XvY) & (Yv`X).
б)F= ((XvY) & (`ZvX)) & (ZvY).

Вариант 4

а) F= A&B&C&`D.

б) F= (AvB) &(`AvB).
Задание 3

По табличному заданию функции найти аналитическое выражение функции и построить логическую схему в соответствии со своим вариантом.

				Вариант 1		Вариант 2			Вариант 3			Вариант 4
	х1	х2	Х3	у1	у2		у3	У4		у5	у6		у7	у8
1	0	0	0	1	0		0	0		1	1		0	0
2	0	0	1	0	1		0	0		0	1		0	0
3	0	1	0	1	0		1	0		0	1		0	1
4	0	1	1	0	0		0	1		1	0		0	0
5	1	0	0	0	0		1	0		1	0		0	1
6	1	0	1	0	1		0	0		0	0		1	0
7	1	1	0	1	1		0	0		0	0		1	1
8	1	1	1	0	0		1	1		0	0		1	0

Контрольные вопросы.

1. Что изучает наука логика?

2. Перечислите и опишите известные вам формы мышления.

3. Опишите и составьте таблицы истинности для известных вам логических функций.

4. Нарисуйте условное обозначение и таблицы истинности для известных вам логических элементов.

5. Как производится синтез комбинационных устройств?
Содержание отчета:

1. 
   Название и цель работы.
   
2. 
   Результат выполнения практических заданий.
   
3. 
   Ответы на контрольные вопросы по указанию преподавателя.
   

Литература

1. 
   Бешенков С.А., Ракитина Е.А. Информатика. Учебник 10 кл. – М., 2010.
   
2. 
   Михеева Е.В. Практикум по информации: учеб. пособие. – М., 2014.
   
3. 
   Михеева Е.В., Титова О.И. Информатика: учебник. – М., 2010.
   
4. 
   Угринович Н.Д. Информатика и информационные технологии. Учебник 10–11 кл. – М., 2010.