Лабораторная работа №3. Лр 3 Решение практических задачах путем сведения их к транспортной задаче Лабораторная работа 3 Тема работы Решение практических задачах путем сведения их к транспортной задаче Цель работы

• Название: Лр 3 Решение практических задачах путем сведения их к транспортной задаче Лабораторная работа 3 Тема работы Решение практических задачах путем сведения их к транспортной задаче Цель работы
• Дата: 22.05.2023
• Размер: 84 Kb.
• Имя файла: Лабораторная работа №3.doc
• Тип: Решение; #1151622

Теория принятия решений курс 3, семестр 6

Л/р № 3 «Решение практических задачах путем сведения их к транспортной задаче»

Лабораторная работа № 3
Тема работы: Решение практических задачах путем сведения их к транспортной задаче
Цель работы: Научиться решать практические задачи в терминах транспортной задачи с привлечением MS Excel.

Ключевые понятия, которые необходимо знать: транспортная задача, открытая модель, закрытая модель, фиктивный поставщик, фиктивный потребитель.

Время выполнения лабораторного занятия: 4 часа.

ХОД РАБОТЫ

Необходимо задачи, представленные ниже, решить в терминах транспортной задачи.

Дополнительное условие в транспортной задаче, не рассмотренное ранее

Транспортная задача с фиксированными доплатами. Предположим, что в открытой транспортной задаче имеет место дефицит продукта и для его устранения в пунктах i = п + 1, ..., k возможно создание новых мощностей d_i.

Пусть переменные z_i = 1, если в пункте i (i = п + 1, ..., k) вво­дятся мощности d_i и z_i = 0, если в пункте i мощности не вводятся. Издержки на ввод мощностей d, в пункте i (i = n + 1, ..., k)составляют и_i.

С учетом возможности создания новых мощностей транспорт­ная задача может быть записана в следующем виде: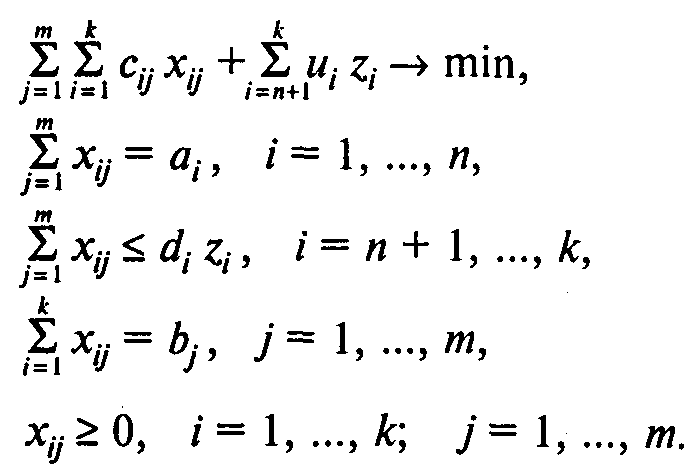



Здесь (5) — целевая функция (минимум затрат на транспортиров­ку и ввод мощностей);

(6) — ограничения по величине предложения в каждом су­ществующем пункте производства;

(7) — ограничения по величине предложения в каждом но­вом пункте производства;

(8) — ограничения по величине спроса в каждом пункте по­требления;

(9) — условия неотрицательности объемов перевозок.

Помимо непрерывных переменных x_ij в модель включены булевы переменные z_i,. Задача (5)—(9) является задачей линейного программирования со «смешанными» переменными.
Задачи для решения

Задача 1. Определение плана перевозок.

Компания, занимающаяся добычей железной руды, имеет четыре карьера. Производительность карьеров соответственно 170, 130, 190 и 200 тыс. т ежемесячно. Железная руда направляется на три принадлежащие этой компании обогатительные фабрики, мощности которых соответственно 250, 150 и 270 тыс. т в месяц.

Транспортные затраты (в тыс. руб.) на перевозку 1 тыс. т руды с карьеров на фабрики указаны в следующей таблице: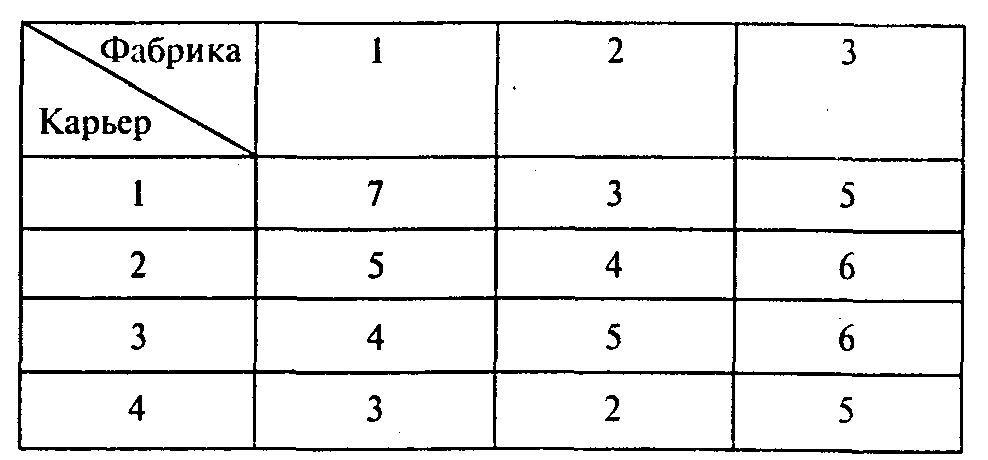



Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транс­портные издержки.

Вопросы:

1. Сколько руды следует перевозить с карьера 1 на обогатительную фабрику 2?

2. Сколько руды следует перевозить с карьера 4 на обогатительную фабрику 1?

3. Какой объем мощностей по добыче руды окажется неис­пользованным?

4. Каковы минимальные совокупные транспортные издержки?
Задача 2. Задача агрегированного планирования.

Компания «Родник» производит и реализует в России концентрат для приготовления фруктового напитка «Солнышко». Производство осуществляется на заводе в Самаре. Отдел сбыта компании «Родник» заключил договоры на поставку концентрата в следующем объеме: апрель — 55 т, май — 70 т, июнь — 75 т. При работе в две смены на собственном оборудовании компания может производить в месяц до 50 т концентрата. Если использовать сверхурочное время, можно увеличить объем производства на 5 т в месяц. В апреле начальный запас концентрата на складе составит 10 т.

Нетрудно видеть, что даже при использовании сверхурочного времени и складских запасов концентрата выполнить договоры не удастся. Поэтому в целях выполнения договорных обязательств принято решение арендовать оборудование акционерного общества «Волжанка». За счет аренды появляется возможность увеличить производство концентрата на 12 т в апреле, на 12 т в мае и на 10 т в июне.

Известно, что производство 1 т концентрата в регулярном режиме двухсменной работы оборудования обходится в 60 тыс. руб. При использовании сверхурочного времени издержки увеличиваются на 20 тыс. руб. за тонну.

Производство 1 т концентрата на арендованном оборудовании обходится в 90 тыс. руб. Издержки хранения 1 т концентрата в течение месяца — 1 тыс. руб.

Договоры предусматривают штрафные санкции в случае несвое­временной поставки концентрата. При задержке поставок на один месяц компания должна будет заплатить штраф в размере 3 тыс. руб. за тонну.

Составьте план использования собственных и арендуемых мощностей для компании «Родник» на каждый месяц второго квартала.

Вопросы:

1. Чему равно значение коэффициента транспортной таблицы, соответствующего регулярному использованию собственных мощностей компании в апреле для удовлетворения спроса на май?

2. Чему равно значение коэффициента транспортной таблицы, соответствующего регулярному использованию собственных мощностей компании в мае для удовлетворения спроса на апрель?

3. При каких минимальных издержках можно выполнить за­ключенные на второй квартал договоры?

4. Какое количество концентрата следует производить в апре­ле на арендуемом оборудовании?

5. Какой размер штрафных санкций за несвоевременную по­ставку концентрата предусмотрен планом?

6. Какая величина запаса концентрата на начало июня преду­смотрена планом?

7. Чему равны издержки выполнения договоров на июнь?
Задача 3. Фирма по прокату автомобилей «Золотое кольцо России» собирает заявки на аренду во всех городах центра России. Клиент имеет возможность получить автомобиль в любом удобном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своем родном городе. Работники фирмы забирают оставленные автомобили и перегоняют их для передачи новым клиентам.

Сейчас 4 автомобиля компании оставлены в Клину, 3 — в Ростове Великом, 6—в Ярославле и 1 — в Серпухове.

Имеются заказы на 5 автомобилей во Владимире, на 3 автомо­биля в Санкт-Петербурге и на 6 автомобилей в Москве.

Расстояния между городами (в км) приведены в следующей таблице: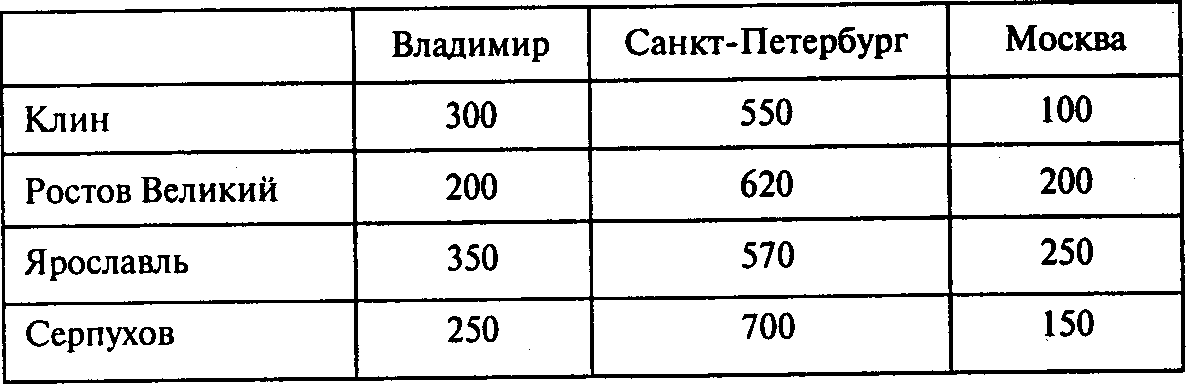



Составьте план, по которому следует перегонять автомобили новым клиентам. Ориентируйтесь на минимизацию расстояния, которое пройдут все перегоняемые автомобили.

Вопросы:

1. Чему равно минимальное расстояние, которое должны прой­ти все автомобили?

2. Сколько автомобилей следует перегнать в Москву из Яро­славля?

3. На сколько увеличится минимальное расстояние, которое должны пройти все автомобили, если дополнительно ста­ло известно, что еще один автомобиль оставлен в Серпухо­ве и еще один клиент появился в Москве?
Задача 4. Компания «Уют» производит пластмассовую мебель для отдыха на открытом воздухе. Основной продукт компании — стулья. Производство находится в Можайске, Наро-Фоминске и Туле. Сейчас на складе в Можайске находятся 7250 стульев, в Наро-Фоминске — 10 150, в Туле — 4350.

Основными потребителями продукции компании «Уют» являются фирмы по оптовой продаже в Москве, Санкт-Петербурге, Минске и Воронеже. Сейчас эти фирмы готовы закупить соответ­ственно 8800, 5800, 2900 и 2100 стульев.

Удельные затраты на перевозку стульев (в руб./шт.) указаны в следующей таблице:



Помогите компании «Уют» составить план транспортировки стульев потребителям.

Вопросы:

1. Чему равны минимальные издержки на перевозку всех стульев?

2. Сколько стульев компания должна перевозить в Москву из Можайска?

3. Какое количество стульев останется на складе в Туле?

4. Стало известно, что для сбыта в Москве не годятся стулья, сделанные в Туле, а для сбыта в Санкт-Петербурге — стулья из Наро-Фоминска. Не подходит цвет стульев. Составьте новый план перевозок с учетом этих условий. На сколько рублей увеличатся при этом совокупные транспортные издержки?
Задача 5. Компания, занимающаяся добычей железной руды, имеет четыре карьера С₁ С₄ (см. пример 1). Производительность карьеров соответственно 170, 150, 190 и 200 тыс. т ежемесячно. Железная руда направляется на три принадлежащие этой компании обогатительные фабрики S₁  S₃, мощности которых соответ­ственно 250, 150 и 270 тыс. т в месяц.

Транспортные затраты (в тыс. руб.) на перевозку 1 тыс. т руды с карьеров на фабрики указаны в следующей таблице: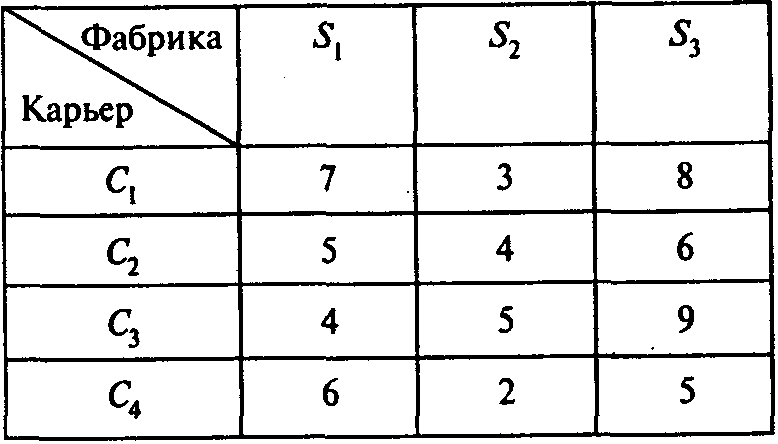



Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транс­портные издержки.

Вопросы:

1. Сколько руды следует перевозить с карьера С₁ на обогатительную фабрику S₂?

2. Сколько руды следует перевозить с карьера С₄ на обогатительную фабрику S₃?

3. Какова общая минимальная стоимость перевозок?

4. Стало известно, что поставки с карьера С₁ на обогатительную фабрику S₂ нужно ограничить объемом 50 тыс. т. К тому же из-за плохого состояния дороги перевозки с карьера С₄на обогатительную фабрику S₃ невозможны. Определите новый план перевозок, учитывающий эти условия. На сколько возрастет стоимость перевозок?

5. Сколько руды следует перевозить с карьера С₄ на обогатительную фабрику S₂ с учетом дополнительной информации?
Задача 6. Фирма «Мойдодыр» оценила спрос на производимый ею лосьон для каждого из четырех следующих месяцев: 100 ящиков в июне, 140 — в июле, 170 — в августе и 90 — в сентябре. Без использования сверхурочного времени фирма может производить до 125 ящиков лосьона в месяц. В сверхурочное время может быть произведено еще 25 ящиков в месяц, но производство каждого ящика обойдется при этом на 1 тыс. руб. дороже. Хранение одного ящика в течение месяца обходится в 100 руб.

Используя модель транспортной задачи, определите, сколько ящиков лосьона следует производить в каждый из этих месяцев, чтобы удовлетворить спрос с минимальными совокупными затратами.

Вопросы:

1. Сколько ящиков лосьона следует произвести в июне?

2. Сколько часов сверхурочного времени следует использовать в сентябре?
Задача 7. Фирма «Время — вперед» хочет разработать план сборки компьютеров. Прогноз спроса на компьютеры для каждо­го квартала следующего года показан в таблице:



При работе в одну смену фирма может каждый квартал собирать 1200 компьютеров. Издержки по сборке одного компьютера составляют 10 тыс. руб. Если ввести вторую смену, то ежеквартально можно собирать еще 800 компьютеров. Однако сборка каждого компьютера во вторую смену обходится дороже — 11 тыс. руб. Компьютер может быть произведен в одном квартале, а сбыт — в любом из последующих кварталов. В этом случае хранение каждого компьютера обходится в 500 руб. за квартал.

Составьте план производства, используя модель транспортной задачи.

Вопросы:

1. Сколько компьютеров следует собрать в первом квартале, чтобы удовлетворить спрос с минимальными совокупными затратами?

2. На сколько процентов следует использовать мощности второй смены в первом квартале?

3. Сколько компьютеров следует собрать во втором квартале?

4. Сколько компьютеров следует собрать во втором квартале во вторую смену для сбыта в третьем квартале?

5. Каковы минимальные издержки?