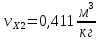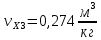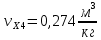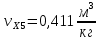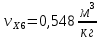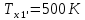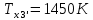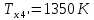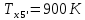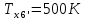Курсовая работа термодинамика. М инистерство науки и высшего образования российской федерации
 Скачать 86.66 Kb. Скачать 86.66 Kb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждение высшего образования «Московский авиационный институт (национальный исследовательский университет)» __________________________________________________________________ Институт «Аэрокосмические наукоемкие технологии и производства» Кафедра «Технология производства и эксплуатации двигателей летательных аппаратов» Курсовая работа по дисциплине «Термодинамика и теплопередача» РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Студент Смирнов Тимур Николаевич Группа Т12О-202Б-18 Руководитель Земляная В.А. Москва – 2019 1. РАСЧЁТ ПАРАМЕТРОВ ВОЗДУХА ( 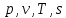 ) ) В УЗЛОВЫХ ТОЧКАХ ЦИКЛА 1.1. Определение начального состояния воздуха в точке 1 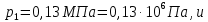 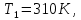 Тогда по уравнению состояния идеального газа удельный объём 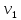 равен: равен: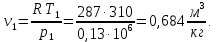 Удельная теплоёмкость идеального газа при постоянном давлении равна: 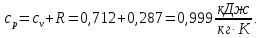 Условно считают, что при нормальных физических условиях ( 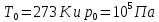 ) энтропия ) энтропия 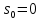 . .Тогда энтропия 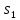 равна изменению энтропии равна изменению энтропии 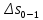 : : 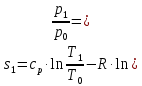 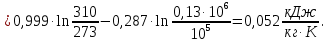 1.2. Определение состояния воздуха в точке 2 Процесс 1-2 изотермический (n = 1), поэтому температура 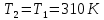 . .Используя соотношение из дополнительных данных 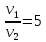 , определим удельный объём , определим удельный объём 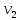 : :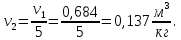 Связь между параметрами газа для изотермического процесса ( 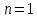 ) имеет следующий вид: ) имеет следующий вид: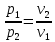 Отсюда давление 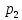 равно: равно: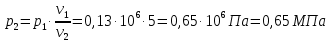 Для изотермического процесса изменение энтропии определяется как: 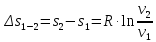 Тогда энтропия 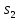 равна: равна: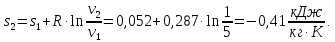 1.3. Определение состояния воздуха в точке 3 Процесс 2-3 изохорный (n = ∞), поэтому объем 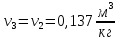 . .Тогда по уравнению связи параметров в изохорном процессе температура 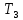 равна: равна: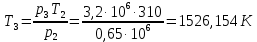 3)Для изохорного процесса изменение энтропии определяется как: 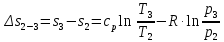 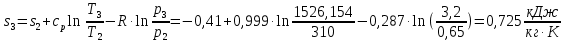 1.4. Определение состояния воздуха в точке 4 Процесс 3-4 политропный ( 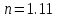 ). ). Так как процесс 4-1 изохорный, 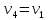 = 0,684 = 0,684 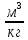 Связь между параметрами газа для адиабатного процесса ( 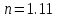 ) имеет вид: ) имеет вид:  Следовательно, давление 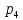 равно: равно: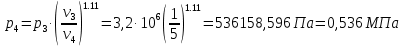 Тогда по уравнению состояния идеального газа температура 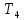 равна: равна: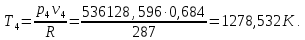 Процесс 3-4 политропный. Для политропного процесса изменение энтропии определяется как: 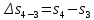 = =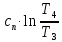 Энтропия 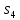 равна: равна: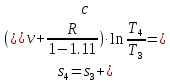  1,061 1,061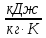 2. РАСЧЁТ ПАРАМЕТРОВ ВОЗДУХА ( 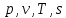 ) ) В ПРОМЕЖУТОЧНЫХ ТОЧКАХ ПРОЦЕССА ЦИКЛА 2.1. Расчёт параметров воздуха ( 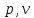 ) для точек ) для точек 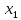 , , 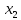 , ,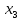 , ,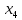 , ,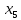 , ,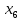  Назначаю промежуточные точки 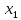 , , 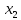 , ,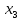 , ,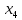 , ,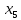 , ,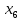 такими, что удельный объём газа в этих точках соответственно равен: такими, что удельный объём газа в этих точках соответственно равен:
Давление газа в точках 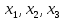 будет определяться по формуле: будет определяться по формуле: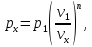 где: 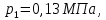 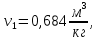 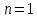 , ,Следовательно: 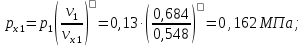 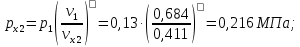 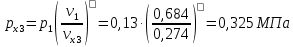 Давление газа в точках 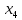 , , 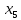 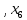 будет определяться по формуле: будет определяться по формуле: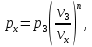 где: 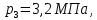 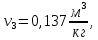 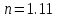 Следовательно:  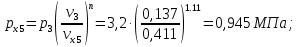 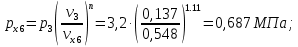 2.2. Расчёт параметров воздуха ( 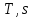 ) для точек ) для точек 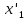 , , 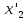 , ,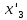 , ,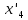 , , , ,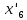  Назначаю промежуточные точки 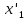 , , 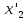 , ,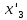 , ,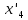 , , , ,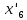 такими, что температура газа в этих точках соответственно равна: такими, что температура газа в этих точках соответственно равна:
Энтропия газа в точках 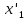 , , 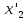 , будет определяться по формуле: , будет определяться по формуле: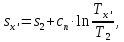 где: 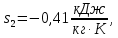 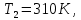 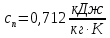 Следовательно: 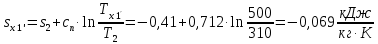 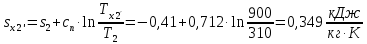 Энтропия газа в точках 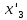 , ,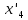 будет определяться по формуле: будет определяться по формуле: 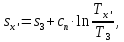 где: 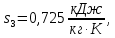 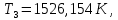 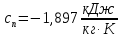 Следовательно: 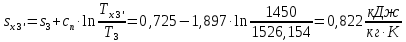 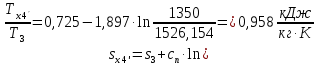 Энтропия газа в точках  , ,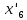 будет определяться по формуле: будет определяться по формуле: 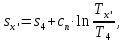 где: 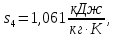 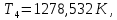 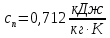 Следовательно: 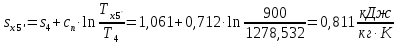 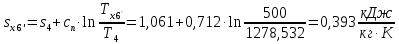 3. ПОСТРОЕНИЕ РАБОЧЕЙ И ТЕПЛОВОЙ ДИАГРАММЫ ЦИКЛА По вычисленным значениям параметров состояния воздуха в узловых и промежуточных точках цикла в масштабе строятся рабочая и тепловая диаграммы цикла. Цикл как в рабочей, так и в тепловой диаграммах, изображается замкнутой кривой, причем направление процессов цикла в этих диаграммах одинаково – по ходу движения часовой стрелки. Все политропные процессы в тепловой диаграмме представляются логарифмическими кривыми, направленными выпуклостью вниз. 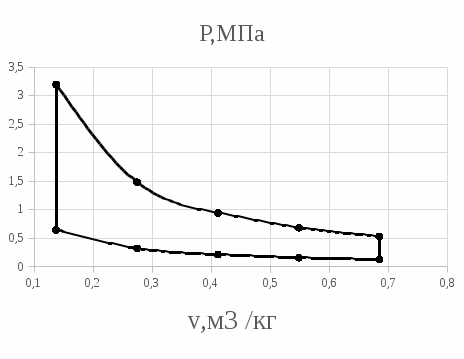 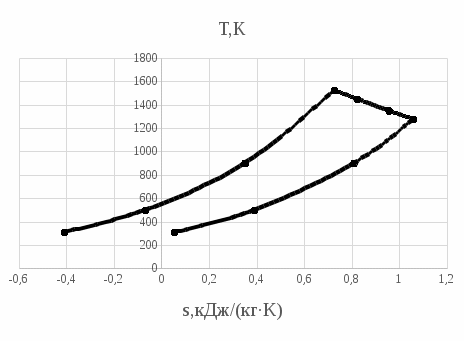 4. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН, ХАРАКТЕРЕЗУЮЩИХ ПРОЦЕССЫ ЦИКЛА 4.1. Определение теплоёмкости воздуха в процессах Теплоёмкость воздуха в рассматриваемом процессе определяется по формуле: 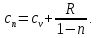 Процесс 1-2 изотермический, 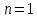 . Тогда: . Тогда: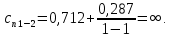 Процесс 2-3 изохорный, 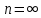 . Тогда: . Тогда: Процесс 3-4 политропный, 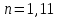 . Тогда: . Тогда: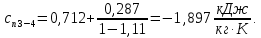 Процесс 4-1 изохорный, 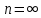 . Тогда: . Тогда: 4.2. Определение работы, производимой воздухом в процессах Работа газа в изотермическом процессе 1-2 равна: 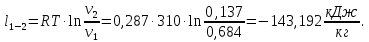 Работа газа в изохорном процессе 2-3 равна: 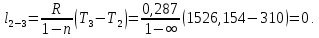 Работа газа в политропном процессе 3-4 равна: 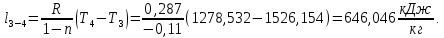 Работа газа в изохорном процессе 4-1 равна:  Полученные величины численно равны площади под кривой соответствующего процесса в рабочей диаграмме. 4.3. Определение изменения внутренней энергии воздуха в процессах Изменение внутренней энергии газа за процесс определяется по формуле:  Изменение внутренней энергии газа за изотермический процесс 1-2 равно: 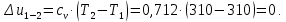 Изменение внутренней энергии газа за изохорный процесс 2-3 равно: 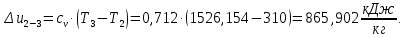 Изменение внутренней энергии газа за политропный процесс 3-4 равно: 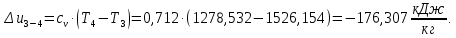 Изменение внутренней энергии газа за изохорный процесс 4-1 равно: 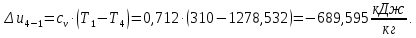 4.4. Определение количества подводимой (отводимой) теплоты в процессах Количество подводимой (отводимой) теплоты за процесс определяется по формуле: 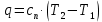 или по первому закону термодинамики. Количество теплоты за изотермический процесс 1-2 равно: 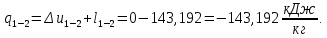 Количество теплоты за изохорный процесс 2-3 равно: 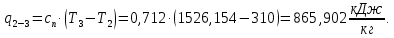 Количество теплоты за политропный процесс 3-4 равно: 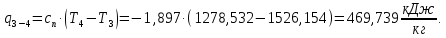 Количество теплоты за изохорный процесс 4-1 равно: 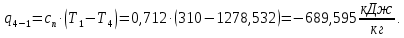 Полученные величины численно равны площади под кривой соответствующего процесса в тепловой диаграмме. 4.5. Определение изменения энтальпии воздуха в процессах Изменение энтальпии газа за процесс определяется по формуле: 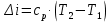 . .Изменение энтальпии газа за изотермический процесс 1-2 равно: 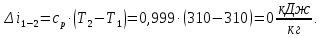 Изменение энтальпии газа за изохорный процесс 2-3 равно:  Изменение энтальпии газа за политропный процесс 3-4 равно: 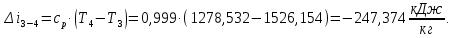 Изменение энтальпии газа за изохорный процесс 4-1 равно: 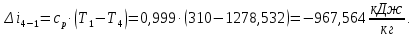 4.6. Определение изменения энтропии воздуха в процессах Изменение энтропии газа за процесс определяется по формуле: 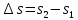 . .Изменение энтропии газа за изотермический процесс 1-2 равно: 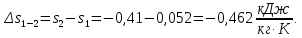 Изменение энтропии газа за изохорный процесс 2-3 равно: 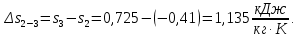 Изменение энтропии газа за политропный процесс 3-4 равно: 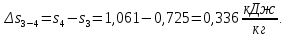 Изменение энтропии газа за изохорный процесс 4-1 равно:  4.7. Определение коэффициента распределения тепла между внутренней энергией и совершаемой работой воздуха в процессах Коэффициент распределения тепла между внутренней энергией и совершаемой работой воздуха за процесс определяется по формуле: 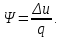 Коэффициент распределения тепла между внутренней энергией и совершаемой работой воздуха за изотермический процесс 1-2 равно: 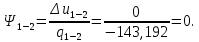 Коэффициент распределения тепла между внутренней энергией и совершаемой работой воздуха за изохорный процесс 2-3 равно: 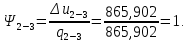 Коэффициент распределения тепла между внутренней энергией и совершаемой работой воздуха за политропный процесс 3-4 равно: 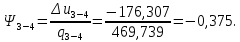 Коэффициент распределения тепла между внутренней энергией и совершаемой работой воздуха за изохорный процесс 4-1 равно: 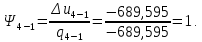 5. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ ЦИКЛ В ЦЕЛОМ 5.1. Определение работы, производимой воздухом за цикл Работа, производимая газом за цикл, определяется алгебраической суммой работ, совершённых газом в отдельных процессах цикла: 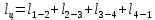 Тогда воздух за один цикл совершает полезную работу, равную: 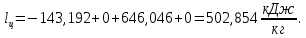 Полученная величина численно равна площади цикла, представленного в рабочей диаграмме. 5.2. Определение количества теплоты, превращённой в работу цикла Количество теплоты, превращённой в работу цикла, определяется алгебраической суммой работ, совершённых газом в отдельных процессах цикла: 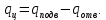  – это теплота, подведённая к газу извне за цикл. Она равна: – это теплота, подведённая к газу извне за цикл. Она равна: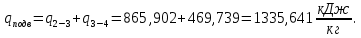 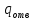 – это теплота, отведённая от газа в охладитель в ходе совершения цикла. Она равна: – это теплота, отведённая от газа в охладитель в ходе совершения цикла. Она равна: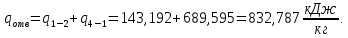 Тогда количества теплоты, превращённой в работу цикла, равно: 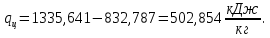 Полученная величина численно равна площади цикла, представленного в тепловой диаграмме. Таким образом, площади цикла в рабочей и тепловой диаграммах имеют одинаковые значения. 5.3. Определение изменения внутренней энергии, энтальпии и энтропии воздуха Изменение внутренней энергии газа за цикл определяется алгебраической суммой изменений внутренней энергии газа за отдельные процессы цикла: 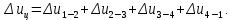 Таким образом, изменение внутренней энергии газа за цикл равно: 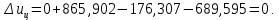 Изменение энтальпии газа за цикл определяется алгебраической суммой изменений энтальпии газа за отдельные процессы цикла: 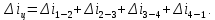 Таким образом, изменение энтальпии газа за цикл равно:  Изменение энтропии газа за цикл определяется алгебраической суммой изменений энтропии газа за отдельные процессы цикла: 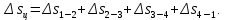 Таким образом, энтропия газа за цикл равно: 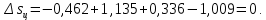 Конечное состояние газа в результате совершения цикла совпадает с начальным состоянием, поэтому изменение внутренней энергии, энтальпии и энтропии воздуха за цикл равно нулю. 5.4. Определение термического КПД цикла Термический КПД цикла определяется отношением полезной работы 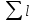 к подведённой теплоте к подведённой теплоте 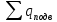 : :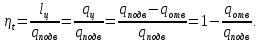 Таким образом, термический КПД цикла равен: 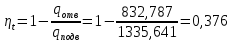 Полученная величина численно равна отношению площади цикла, представленного в тепловой диаграмме, к площади, соответствующей количеству подводимой теплоты. Термический КПД цикла характеризует степень совершенства преобразования теплоты в работу. Совершенство произвольного обратимого цикла оценивается сравнением его термического КПД с термическим КПД обратимого цикла Карно, осуществляемого между крайними ( 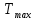 и и  ) температурами рассматриваемого цикла. Цикл Карно имеет максимальный термический КПД для заданного интервала температур и определяется как: ) температурами рассматриваемого цикла. Цикл Карно имеет максимальный термический КПД для заданного интервала температур и определяется как: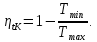 Для данного цикла:  , ,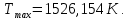 Тогда цикл Карно имеет максимальный термический КПД для заданного интервала температур, равный 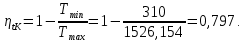 Для того чтобы определить, насколько рассматриваемый цикл приближается к соответствующему циклу Карно, необходимо определить, насколько термический КПД рассматриваемого цикла меньше термического КПД цикла Карно. Это сравнение производится по формуле: 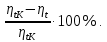 В данном случае рассматриваемый цикл приближается к соответствующему циклу Карно, осуществляемому между крайними ( 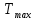 и и  ) температурами рассматриваемого цикла на: ) температурами рассматриваемого цикла на: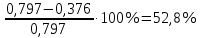 |