прпрапор. Магические квадраты

• Название: Магические квадраты
• Анкор: прпрапор
• Дата: 01.02.2023
• Размер: 16.74 Kb.
• Имя файла: 8.docx
• Тип: Документы; #916378

Магические квадраты

Магическим «n²-квадратом» назовем квадрат, разделенный на n² клеток, заполненных первыми n² натуральными числами так, что суммы чисел, стоящих в любом горизонтальном или вертикальном ряду, а также на любой из диагоналей квадрата, равны одному и тому же числу S_n=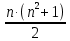

Если одинаковы лишь суммы чисел, стоящих в любом горизонтальном и вертикальном ряду, то квадрат называется полу магическим.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

2	7	6
9	5	1
4	3	8

6	7	2
1	5	9
8	3	4

Магический 4²-квадрат наименованием Дюрера, математика и художника XVI века, изобразившего квадрат на известной картине «Меланхолия».

Кстати, два нижних средних числа этого квадрата образуют число 1514- дату создания картины.

Существует лишь восемь девятиклеточных квадратов. Два из них, являющиеся зеркальным отражением друг друга, приведены на рисунке; остальные шесть могут быть получены из этих квадратов вращением их вокруг центра на 90°, 180°, 270°.

2. Нетрудно полностью исследовать вопрос о магических квадратах при n=3. Действительно, S3 = 15, и существует лишь восемь способов представления числа 15 в виде суммы различных чисел(от единицы до девяти):

15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6.

Заметим, что каждое из чисел 1, 3, 7, 9 входит в две, а каждое из чисел 2, 4, 6, 8 - в три указанные суммы и лишь число 5 входит в четыре суммы. С другой стороны, из восьми трехклеточных рядов: трех горизонтальных, трех вертикальных и двух диагональных - через каждую изугловых клеток квадрата проходит по три, черезцентральную клетку по четыре и черезкаждую из остальных клетокпо дваряда. Следовательно, число 5 должно обязательно стоять вцентральной клетке, числа 2, 4, 6, 8 - в угловых клетках, ачисла 1, 3. 7,9 - в остальных клетках квадрата.