Отработка элтехзника. Магнитные цепи Введение
 Скачать 87.88 Kb. Скачать 87.88 Kb.
|
Магнитные цепиВведениеВ конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т.д.) входят магнитные цепи. Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и, вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты. В конструктивном отношении магнитные цепи выполняют разветвлёнными и неразветвлёнными, причём применение того или иного вида цепи определяется в основном назначением электромагнитного устройства. Основные определенияКак известно из курса физики, вокруг проводника с током появляется магнитное поле. Интенсивность магнитного поля характеризуется векторной величиной: напряженностью магнитного поля где μ0 - абсолютная магнитная проницаемость, Гн/м; μ - относительное значение магнитной проницаемости, безразмерная величина; μ0 = 4π·10-7 Гн/м. В зависимости от величины относительной магнитной проницаемости, все вещества делятся на три группы. К первой группе относятся диамагнетики: вещества, у которых μ< 1. Ко второй группе относятся парамагнетики, вещества с μ >1. К третьей группе относятся ферромагнетики, вещества с μ >> 1. К ферромагнетикам принадлежат железо, никель, кобальт и многие сплавы из неферромагнитных веществ. Магнитной цепью называется совокупность устройств, содержащих ферромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы, магнитного потока. Магнитным потоком называется поток вектора магнитной индукции через поверхность S 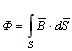 . .Магнитный поток измеряется в веберах (Вб). Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током). Магнитодвижущая сила электромагнита где I - ток, протекающий в катушке; W - число витков катушки. В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности. Свойства ферромагнитных материаловПоместим ферромагнитный материал внутри катушки с током. Сначала, с увеличением напряженности намагничивающего поля, магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. 9.1. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал. 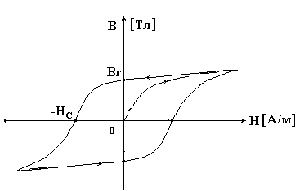 Рис. 9.1 Значение магнитной индукции при напряженности намагничивающего поля, равном нулю, называется остаточной магнитной индукцией Br, или остаточной намагниченностью. Напряженность магнитного поля НС при В = 0 называется коэрцитивной силой. Ферромагнитные материалы с большим значением коэрцитивной силы ( Ферромагнитные материалы с малым значением коэрцитивной силы ( Таким образом, зависимости B = f(H) у ферромагнитных материалов нелинейные. Эти зависимости приводятся в справочниках в табличной форме или в виде кривых, называемых кривыми намагничивания. Переменный магнитный поток в катушке с магнитопроводом. Конструкции магнитопроводов и их функциональные назначения в электротехнических устройствах переменного тока весьма разнообразны. Рассмотрим катушки с неразветвлёнными магнитопроводами из ферромагнитного материала.                            e=U el i ф Рис.1 У катушки с магнитопроводом, подключенной к источнику синусоидального напряжения или: Из этого уравнения найдём закон изменения во времени магнитного потока. Так как: то: Постоянная интегрирования А равна некоторому постоянному магнитному потоку, которого нет в магнитопроводах аппаратов переменного тока в установившемся режиме работы. Следовательно постоянная А = 0 и магнитный поток6 где: т.е. при синусоидальном напряжении между выводами катушки магнитный поток в магнитопроводе также синусоидальный. Так как действующие значения напряжения U между выводами катушки и ЭДС самоиндукции EL (1), то из (4) получим: Последнее соотношение применяют для расчётов ЭДС, индуктируемых в обмотках трансформаторов; поэтому его часто называют уравнением трансформаторной ЭДС. При определении магнитного потока не учитывались активное сопротивление обмотки и наличие магнитных линий поля катушки, которые частично и полностью замыкаются помимо магнитопровода. Для выявления характера изменения магнитного потока в магнитопроводе во времени это не имеет сколько-нибудь существенного значения. Но при других расчётах активное сопротивление обмотки и магнитные линии поля катушки, которые неполностью замыкаются по магнитопроводу, часто надо учитывать. Соотношения (3; 4; 5) можно рассматривать лишь как ориентировочно связывающие действующие значения напряжения U между выводами катушек и ЭДС самоиндукции EL с амплитудой магнитного потока Фм в магнитопроводе и числом витков w катушки. Расчет магнитных цепейОсновным законом, используемым при расчетах магнитных цепей, является закон полного тока. Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда векторное произведение в формуле (6) можно заменить произведением скалярных величин H·dl. В практических расчетах интеграл где l1, l2, …, ln - длины участков магнитной цепи; H1·l1, H2·l2 - магнитные напряжения участков цепи. Магнитным сопротивлением участка магнитной цепи называется отношение магнитного напряжения рассматриваемого участка к магнитному потоку в этом участке где S - площадь поперечного сечения участка магнитной цепи, l - длина участка. Рассмотрим расчет магнитной цепи, изображенной на рис. 2. 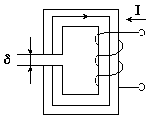 Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S. Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S. lср - длина средней силовой линии магнитного поля в магнитопроводе; δ - толщина воздушного зазора. На магнитопроводе размещена обмотка, по которой протекает ток I. рис. 2. Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Определим магнитную индукцию в магнитопроводе По кривой намагничивания найдем значение напряженности магнитного поля H, соответствующее величине В. Напряженность магнитного поля в воздушном зазоре Магнитодвижущая сила обмотки При обратной задаче расчета магнитной цепи по заданному значению магнитодвижущей силы требуется определить магнитный поток. Расчет такой задачи выполняется с помощью магнитной характеристики цепи F = f(Ф). Для построения такой характеристики необходимо задаться несколькими значениями Ф и найти соответствующие значения F. С помощью магнитной характеристики по заданной магнитодвижущей силе определяется магнитный поток. |
