Мұғалімнің аты-жөні:
|
|
Пән/Сынып:
|
10б сынып, ЖМБ
|
Күні:
|
14.10.
|
Тарау немесе бөлім атауы:
|
10.1С Кері тригонометриялық функциялар
|
Сабақтың тақырыбы:
|
Арксинус, арккосинус, арктангенс және арккотангенс .
|
Оқу мақсаты:
|
10.2.3.3 - арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын білу және олардың мәндерін таба білу;
|
Бағалау критериі:
|
Функциялардың графиктерін түрлендіріп салуды үйренеді;
Қасиеттерін есеп шығаруда қолдана алады;
Функция графиктерін сауатты салуды меңгереді
|
Саралап оқыту тапсырмалары
|
Ұжымдық жұмыс
Жаңа тақырыптың түсіндірілуі
Сабақ мақсаты мен бағалау критерийлерін таныстыру;
Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату
|
Бірлескен жұмыс (1,2 тапсырма)
Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету
Бекітуге арналғантапсырмаларды орындату;
Тапсырмалардың жауаптарын жазу.
|
Жеке жұмыс
Тапсырманы ұсыну, оқушылар өз бетімен орындауы
|
Уақыты
|
Кезең
дері
|
Педагогтің әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
5 минут
|
Ұйымдас тыру
|
Сәлеметсіздерме!
Бүгін, Арксинус, арккосинус, арктангенс және арккотангенс тақырыбын қарастырамыз.
Бүгінгі сабақта меңгеретініңіз:
- арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын білу және олардың мәндерін таба білу;
Ұйымдастыру. Үй жұмысын тексеру.
|
Амандасады.
Үй тапсырмасын айтады.
|
|
Оқулық
|
15 мин
|
Негізгі бөлім
|
Оқушыларды сабақты меңгеруге қажетті материалдарды қайталауға :
тригонометриялық шеңбер;
тригонометриялық функциялардың 0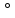 ,30 ,30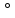 ,45 ,45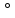 ,60 ,60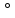 ,90 ,90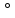 -ғы мәндері; -ғы мәндері;
тригонометриялық функциялардың анықталу облысы мен мәндерінің жиыны.
Сабақтың тақырыбы және мақсатымен таныстыру, күтілетін нәтижені айқындау.
Оқушыларға келесі тапсырмаларды ұсыну арқылы проблемалық ахуал туғызу:
Берілгені:а)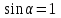 ; б) ; б)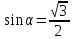 ; в) ; в) 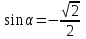 ; г) ; г) 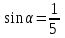 . .
Кері тригонометриялық функциялар (аркфункциялар; лат. arc — доға) — тригонометриялық функцияларға кері функциялар.
Керi тригонометриялық функцияларға алты функция жатады (әр тригонометриялық функцияларға сәйкес)
арксинус (белгіленуі: 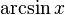 ) )
арккосинус (белгіленуі: 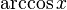 ) )
арктангенс (белгіленуі: 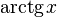 ) )
арккотангенс (белгіленуі: 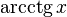
арксеканс (белгіленуі: 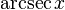 ) )
арккосеканс (белгіленуі: 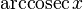 ) )
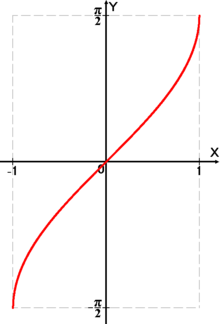
Арксинус у= sin x функциясына кері функцияны у=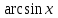 деп белгілеп , «арксинус х» деп оқиды. деп белгілеп , «арксинус х» деп оқиды.
y = sinx функциясы 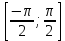 кесіндісінде анықталған, бірсарынды өспелі және -1 –ден 1-ге дейінгі мәндерді қабылдайды. Демек , кесіндісінде анықталған, бірсарынды өспелі және -1 –ден 1-ге дейінгі мәндерді қабылдайды. Демек ,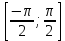 кесіндісінде y = sinx функциясына кері функция бар. у кесіндісінде y = sinx функциясына кері функция бар. у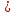 аrcsin х деп белгіленеді. аrcsin х деп белгіленеді.
Арксинус - синуске кepi функция.
Арккосинус y=cos x функциясына кері функцияны y=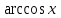 деп белгілеп, «арккосинус х» деп оқиды. деп белгілеп, «арккосинус х» деп оқиды.
y=cosx функциясы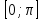 кесіндісінде анықталған, бірсарынды кемімелі және -1 –ден 1-ге дейінгі мәндерді қабылдайды. Демек , кесіндісінде анықталған, бірсарынды кемімелі және -1 –ден 1-ге дейінгі мәндерді қабылдайды. Демек ,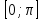 кесіндісінде y = cosx функциясына кері функция бар. у кесіндісінде y = cosx функциясына кері функция бар. у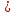 аrccos х деп белгіленеді. аrccos х деп белгіленеді.
Арккосинус - косинуске кepi функция.
Қасиеттері:
1) D ( arccos x) = 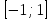 (анықталу облысы), (анықталу облысы),
2) E( arccos x) = 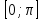 (мәндер облысы). (мәндер облысы).
3) Функция жұп та, тақ та емес
4) Функция 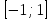 кесіндісінде бірсарынды кемімелі болып табылады. кесіндісінде бірсарынды кемімелі болып табылады.
Кез келген х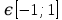 үшін cos(arccos x) =x теңдігі орындалады және arccos x үшін cos(arccos x) =x теңдігі орындалады және arccos x 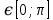
Кез келген х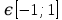 үшін arccos x + arccos (-x) = үшін arccos x + arccos (-x) = 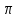 немесе немесе
arccos (-x) =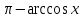
|
Қосымша ақпарат көздерін пайдалана отырып түсінеді
Тақырып бойынша ресурстарды қарап, танысады
Қасиеттері:
1) D ( arcsin x) = 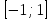 (анықталу облысы), (анықталу облысы),
2) E( arcsin x) = 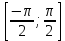 (мәндер облысы). (мәндер облысы).
3)Tақ функция , яғни arcsin(-x) = - arcsinx
4) Функция 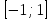 кесіндісінде бірсарынды өспелі болып табылады. кесіндісінде бірсарынды өспелі болып табылады.
Кез келген х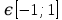 үшін sin(arcsin x) =x теңдігі орындалады және үшін sin(arcsin x) =x теңдігі орындалады және
arcsin x 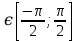
Мысалдар:
arcsin 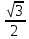 = = 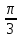 ; Өйткені sin ; Өйткені sin 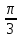 = =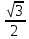 , , 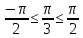
arcsin (-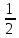 )= - arcsin )= - arcsin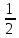 =- =- 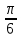 ; Өйткені sin ; Өйткені sin 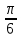 = =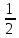 , , 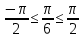
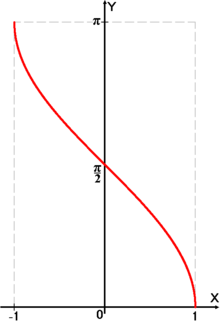
Мысалдар:
arccos 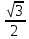 = = 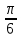 ; Өйткені cos ; Өйткені cos 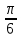 = =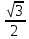 , 0 , 0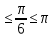
arccos 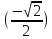 = = 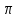 - arccos - arccos 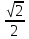 = = 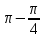 = =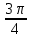 ; Өйткені cos ; Өйткені cos 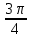 = =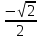 , 0 , 0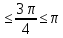
3 2 2
|
«Екі жұлдыз бір ұсыныс»
|
Слайд
Оқулық
|
20 мин
|
Бекіту тапсырма лары
|
Тапсырма. №1. Есептеңіздер
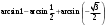 = =
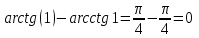
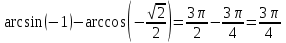
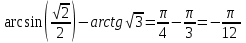
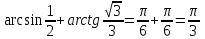
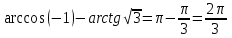
Оқулықтан №15.1, №15.2.
|
Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, топтық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды.
Өз бетімен жұмыс.
Тест тапсырмалары.
№1-№5.
|
Дескриптор:
-Берілген тригонометриялық функцияға кері функця жаза алады.
-Кері тригонометриялық өрнектің мәнін таба алады.

ҚБ «Екi жұлдыз бiр тiлек» әдiсi .Бiрiн-бiрi бағалау
|
Интернет ресурстары
Жалпы білім беретін мектептің 10–сыныбына арналған оқулық.
|
|
Жеке жұмыс
|
№15.6
|
Тапсырмаларды орындайды.
|
|
|
5 минут
|
|
Бүгінгі сабақта:
- арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын біледі және олардың мәндерін таба біледі.
Кері байланыс:
Білдім
|
Білемін
|
Білгім келеді
|
|
|
|
Үйге тапсырма. №15.3.
|
Тақырыпты меңгергенін анықтау
|
Кері байланыс
|
|
 Скачать 88.93 Kb.
Скачать 88.93 Kb.