Курсовая по Машине Тьюринга. ИЗ-12_2020_вариант_19. Машина Тьюринга

• Название: Машина Тьюринга
• Анкор: Курсовая по Машине Тьюринга
• Дата: 22.06.2021
• Размер: 17.85 Kb.
• Имя файла: ИЗ-12_2020_вариант_19.docx
• Тип: Курсовая; #220232

Федеральное агентство морского и речного транспорта
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«государственный университет морского и речного флота
имени адмирала с.о. макарова»

––––––––––––––––––––––––––––––––––––––––––––––––––––––––

ИНСТИТУТ ВОДНОГО ТРАНСПОРТА
КАФЕДРА «КОМПЛЕКСНОЕ ОБЕСПЕЧЕНИЕ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ»


КУРСОВАЯ РАБОТА

по Математической логике и теории алгоритмов
на тему:

Машина Тьюринга

вариант № 19

Выполнил: студент группы ИЗ–12
____Бутятин Иван Витальевич____ _________________

(фамилия, имя, отчество) (подпись)
Руководитель:

_______Нырков Анатолий Павлович ____ _________________

(фамилия, имя, отчество) (подпись)
Представлена на кафедру: «___» _____________ 2020 г.


Санкт – Петербург

2020

Описание Машины Тьюринга

Машина Тьюринга - это абстрактный исполнитель. Предложена Аланом Мэтисоном Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина состоит:

1. 
   Внешний алфавит A={a₀, a₁, a₂, ... , a_n};
   
2. 
   Внутренний алфавит Q={q₁, q₂, q₃, ..., q_m} - множество состояний;
   
3. 
   Множество управляющих символов {R, L, C}
   
4. 
   Бесконечная в обе стороны лента, разделённая на ячейки, в каждую из которых в любой дискретный момент времени может быть записан только один символ алфавита A;
   
5. 
   Управляющее устройство, способное находиться в одном из множеств состояний.
   

Свой вариант задания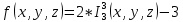



Построить машину Тьюринга, правильно вычисляющую функцию. Аргументы и значение функции представляются в унарном коде, аргументы разделяются пустой ячейкой (символ 0). Если значение функции не является неотрицательным целым числом, то машина Тьюринга не приходит в конечное состояние q₀.

Описание алгоритма машины Тьюринга, реализующей задание

С q₁ по q₈ машина вычисляет 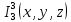доходя до z, машина удаляет все предыдущие числа и возвращается к оставшемуся числу.

С q₉ по q₁₈ машина умножает последние число на 2. Перед умножаемым число ставятся две 1, потом у умножаемого числа убирают с начала одну единицу, до того момента, пока машина не сотрёт первое число. После этого у полученного числа стирают в начале одну единицу.

С q₁₉ по q₂₃ машина вычитает от полученного числа 3. Машина стирает у полученного числа 3 единицы в начале.

Команды машины Тьюринга для выполнения заданного варианта

q₁ 1 → q₂ 1 R

q₂ 0 → q₃ 0 R

q₂ 1 → q₂ 1 R

q₃ 0 → q₄ 0 L

q₃ 1 → q₂ 1 R

q₄ 0 → q₅ 0 L

q₅ 1 → q₅ 1 L

q₅ 0 → q₆ 0 L

q₆ 0 → q₈ 0 R

q₆ 1 → q₇ 0 L

q₇ 1 → q₇ 0 L

q₇ 0 → q₆ 0 L

q₈ 0 → q₈ 0 R

q₈ 1 → q₉ 1 R

q₉ 0 → q₁₀ 0 R

q₉ 1 → q₉ 1 R

q₁₀ 0 → q₁₁ 1 R

q₁₀ 1 → q₁₁ 1 R

q₁₁ 0 → q₁₂ 1 R

q₁₁ 1 → q₁₀ 1 R

q₁₂ 0 → q₁₃ 0 L

q₁₃ 1 → q₁₄ 1 L

q₁₄ 0 → q₁₅ 0 L

q₁₄ 1 → q₁₄ 1 L

q₁₅ 0 → q₁₆ 0 R

q₁₅ 1 → q₁₄ 1 L

q₁₆ 0 → q₁₇ 0 R

q₁₇ 1 → q₁₈ 0 R

q₁₈ 0 → q₁₉ 0 R

q₁₈ 1 → q₉ 1 R

q₁₉ 1 → q₂₀ 0 R

q₂₀ 1 → q₂₁ 0 R

q₂₁ 1 → q₂₂ 0 R

q₂₂ 1 → q₂₃ 0 R

q₂₂ 0 → q₀ 0 C

Литература для подготовки

1. Нырков А.П., Нырков А.А. Введение в общую теорию алгоритмов. – СПб.: ГУМРФ имени адмирала С.О. Макарова, 2013. – 43 c.

2. Нырков А.П., Нырков А.А. Математическая логика: алгебра и исчисление высказываний. – СПб.: ГУМРФ имени адмирала С.О. Макарова, 2013. – 70 c.

3. Нырков А.П., Нырков А.А., Соколов С.С. Алгебра и исчисление высказываний. – СПб.: СПГУВК, 2008. – 112 с.

4. Гаврилов Г.П., Сапожников А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2004. – 416 с.