Типовик по математической статистике. Математическая статистика
 Скачать 294.11 Kb. Скачать 294.11 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Омский государственный технический университет» Кафедра «Высшая математика» Типовой расчет по дисциплине «Высшая математика» Тема: «Математическая статистика» Выполнил: ст-т группы ХТ-172 Слободян В.А. Проверила: старший преподаватель, Евсеева С.И. Оценка, замечания: ______________________________________________________________________________ (лата, подпись) Омск 2018 ЛАБОРАТОРНАЯ РАБОТА 1 «Основы статистического описания» 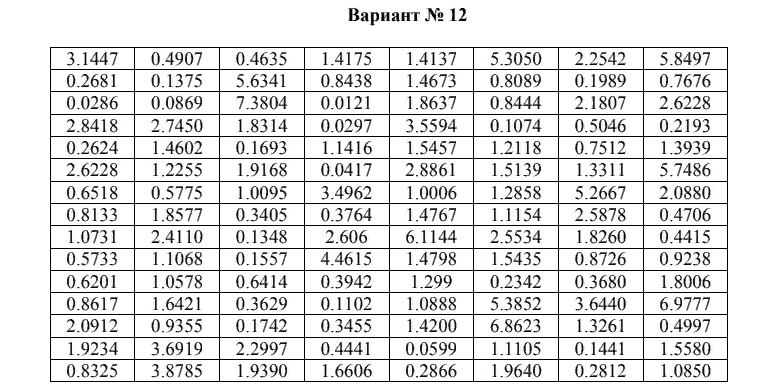 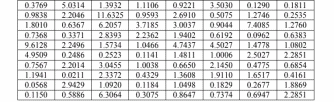 Дана выборка, содержащая 200 элементов. Упорядочим выборку. Наименьшее число равно 0,0121, наибольшее число равно 11,6325. Интервал (0; 12) разделим на 20 равных частей. Границы интервалов занесем в графу 2 расчетной таблицы. Число элементов, попавших в i –й интервал, занесем в графу 3. Два числа – 7.4085 7.4085, 11.6325, резко отличающиеся от других и полученные, видимо, за счет грубых ошибок опыта, можно отбросить. Таким образом, n =198. Объединим интервалы так, чтобы новые интервалы содержали не менее 8-10 элементов. Новые границы интервалов, а также число элементов, попавших в уточненные интервалы, поместим в графы 4 и 5. В графу 6 поместим частоты попаданий в каждый интервал. В графу 7 поместим середины каждого интервала. Далее расчетная таблица заполняется в соответствии с описанием работы. По полученным данным строится график эмпирической функции распределения и гистограмма. По формулам (4), (6), (7) вычисляются выборочные среднее значение выборки, дисперсия, коэффициент асимметрии и эксцесс. Предварительно удобно вычислить следующие суммы: 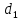 = =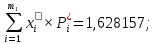 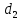 = =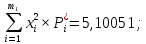 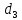 = =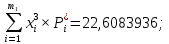 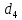 = =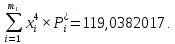 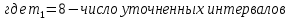 . .Тогда 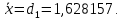 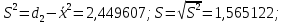 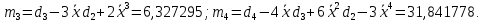 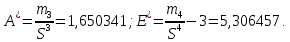 Выборочную медиану 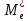 определим по всей упорядоченной выборке следующим образом: определим по всей упорядоченной выборке следующим образом: 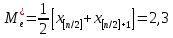 Расчетная таблица 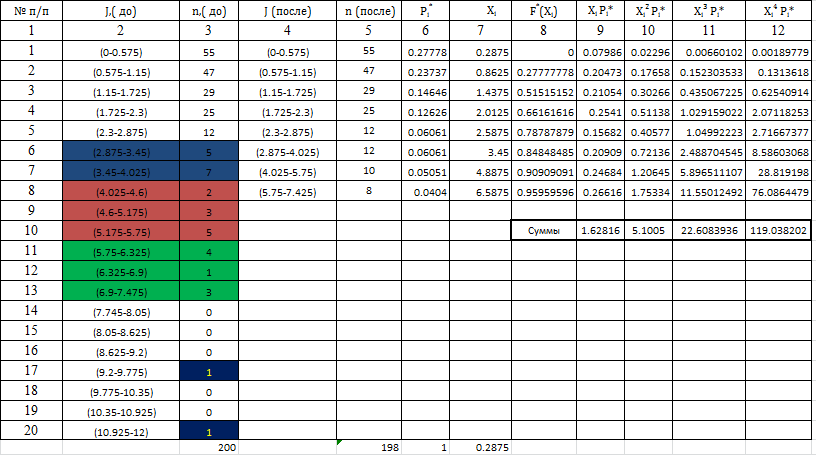 График эмпирической функции 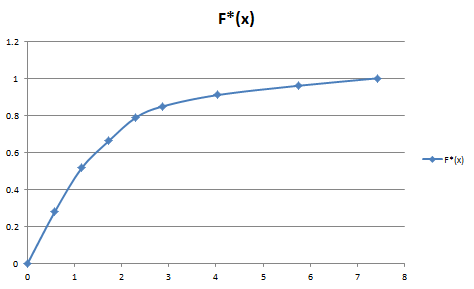 ЛАБОРАТОРНАЯ РАБОТА 2 ЛАБОРАТОРНАЯ РАБОТА 2«Проверка статистической гипотезы о законе распределения генеральной совокупности по выборке» Дана выборка, содержащая 200 элементов. Упорядочим выборку. Наименьшее число равно 0,3624, наибольшее число равно 11,2085. Интервал (0,362; 11,210) разделим на 20 равных частей. Границы интервалов занесем в графу 2 расчетной таблицы. Число элементов, попавших в i –й интервал, занесем в графу 3. Два числа – 10,1891, 11,2085, резко отличающиеся от других и полученные, видимо, за счет грубых ошибок опыта, можно отбросить. Таким образом, n =198. Объединим интервалы так, чтобы новые интервалы содержали не менее 8-10 элементов. Новые границы интервалов, а также число элементов, попавших в уточненные интервалы, поместим в графы 4 и 5. В графу 6 поместим частоты попаданий в каждый интервал. По полученным данным построим гистограмму. В графу 7 поместим середины каждого интервала. Вид гистограммы дает право выдвинуть гипотезу о нормальном законе распределения генеральной совокупности с параметрами a и 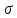 . .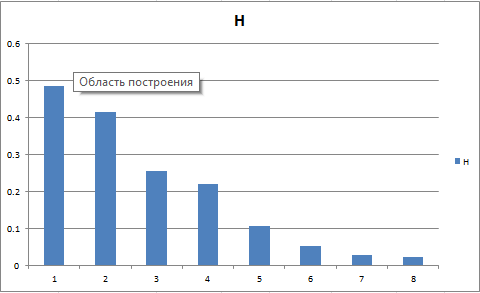 Для удобства значения 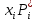 поместим в графу 8, значения поместим в графу 8, значения 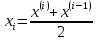 предварительно были помещены в графу 7. Оценка математического ожидания предварительно были помещены в графу 7. Оценка математического ожидания 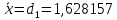 . Для вычисления величины . Для вычисления величины 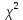 - меры расхождения теоретического и статистического распределений - вычислим теоретические вероятности попаданий значений случайной величины в i – ый интервал по формуле - меры расхождения теоретического и статистического распределений - вычислим теоретические вероятности попаданий значений случайной величины в i – ый интервал по формуле 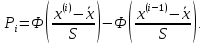 Значения Значения 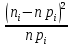 для каждого i занесем в графу 11. Вычисленное хначение для каждого i занесем в графу 11. Вычисленное хначение 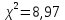 . .В данном примере по выборке определен 1 параметр. Следовательно, r = 1 и число степеней свободы распределения k = 8 − 1 −1 = 6. Зададимся уровнями значимости 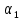 = 0,01 и = 0,01 и 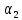 = 0,05. По таблице квантилей распределения Пирсона находим = 0,05. По таблице квантилей распределения Пирсона находим 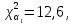 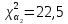 . Вычисленное значение . Вычисленное значение 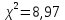 меньше меньше 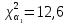 и и 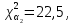 следовательно, гипотеза не отвергается уровнями значимости следовательно, гипотеза не отвергается уровнями значимости 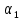 = 0,01 и = 0,01 и 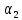 = 0,05. = 0,05.Расчетная таблица 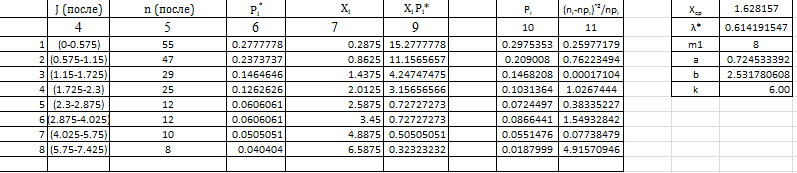 |
