Математические методы в экономике и управлении
 Скачать 1.41 Mb. Скачать 1.41 Mb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт промышленного менеджмента, экономики и торговли Высшая школа управления и бизнеса КУРСОВая работа Применение моделей линейной оптимизации по дисциплине «Математические методы в экономике и управлении» Выполнил студент гр. 237331/0002 Тулубаев Р.И. Руководитель доцент, к.ф.-м.н. А.Л. Кутузов «__» ______2019 г. Санкт-Петербург 2019
Требуется определить план выпуска четырех видов продукции, обеспечивающий максимальную прибыль от ее реализации. На изготовление этой продукции расходуются трудовые ресурсы, сырье и финансы. С учетом рыночного спроса и производственно-технологических возможностей заданы предельные границы выпуска каждого вида продукции. Эти границы, наличие и нормы расхода ресурсов, а также маржинальная прибыль (разность между выручкой и переменными издержками) на единицу продукции приведены в таблице: A)
3≤ 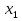 ≤59, ≤59,1≤ 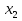 , ,1≤ 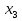 ≤57, ≤57,2≤ 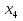 ≤58, ≤58,Обозначив количество выпускаемых изделий через 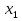 , , 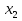 , , 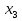 , , 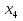 , соответственно, а целевую функцию – валовую маржинальную прибыль – через F, построим математическую модель задачи: , соответственно, а целевую функцию – валовую маржинальную прибыль – через F, построим математическую модель задачи:F=70 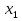 +60 +60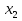 +110 +110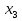 +140 +140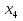 →max →max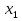 +2 +2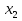 + +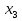 +2 +2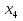 ≤73, ≤73,7 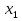 +4 +4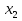 +5 +5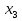 +4 +4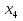 ≤134, ≤134,5 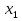 +7 +7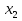 +9 +9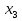 +8 +8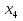 ≤154, ≤154,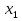 , , 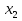 , , 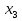 , , 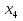 ≥0. ≥0.B) Табличная модель: 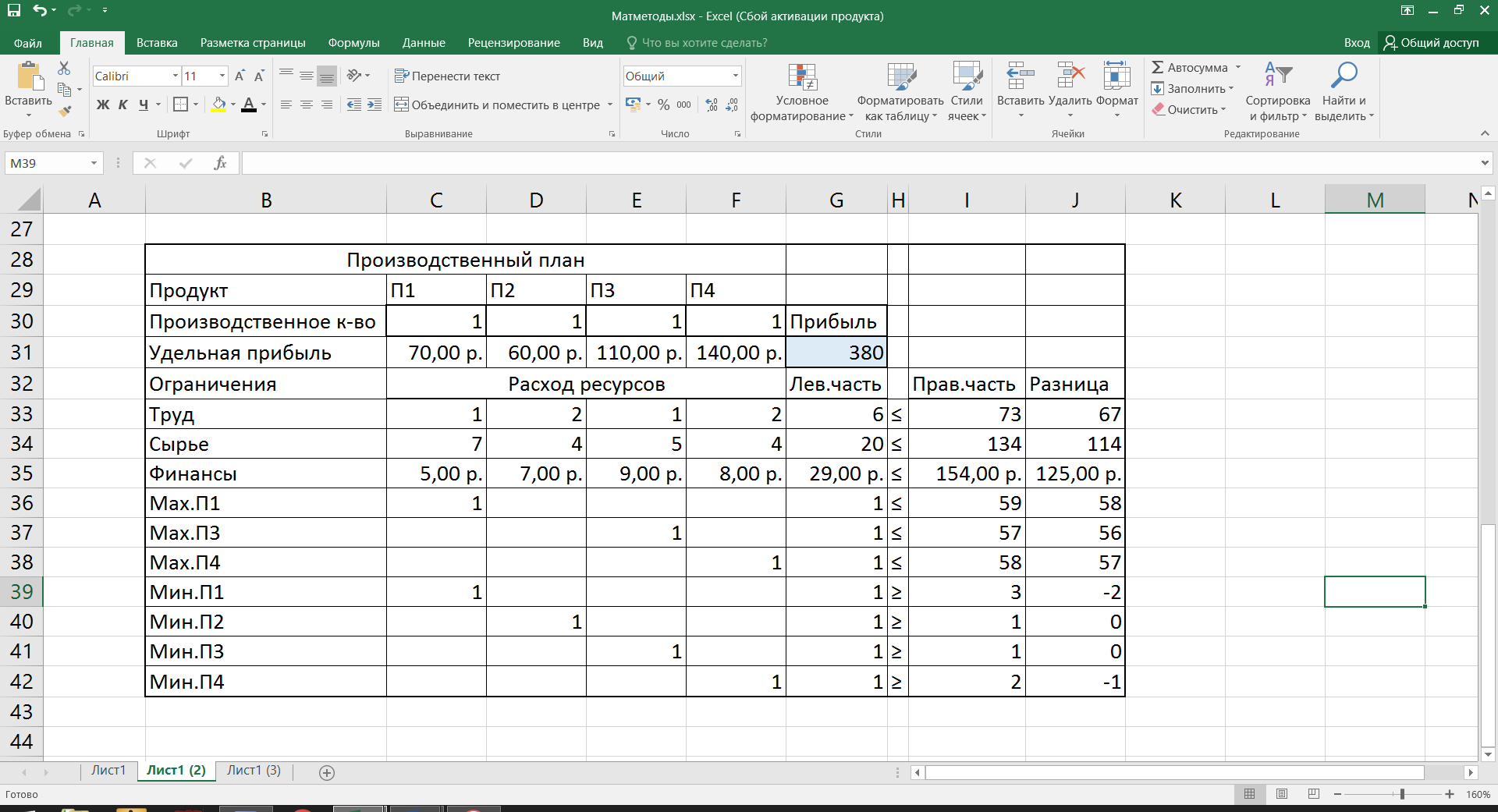 Рис. 1. Модель с введенными формулами. 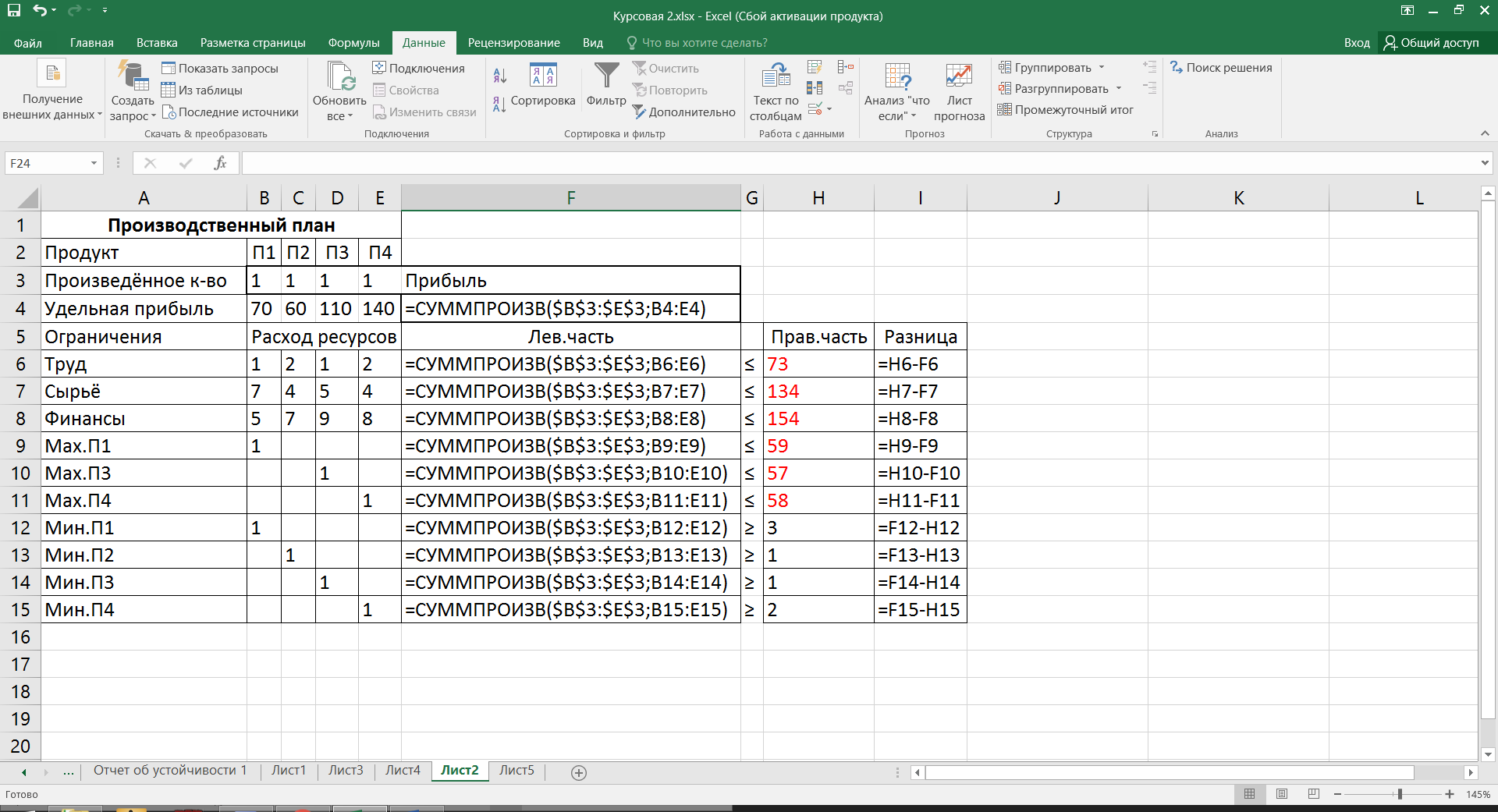 Рис 2. Модель с отображением формул. 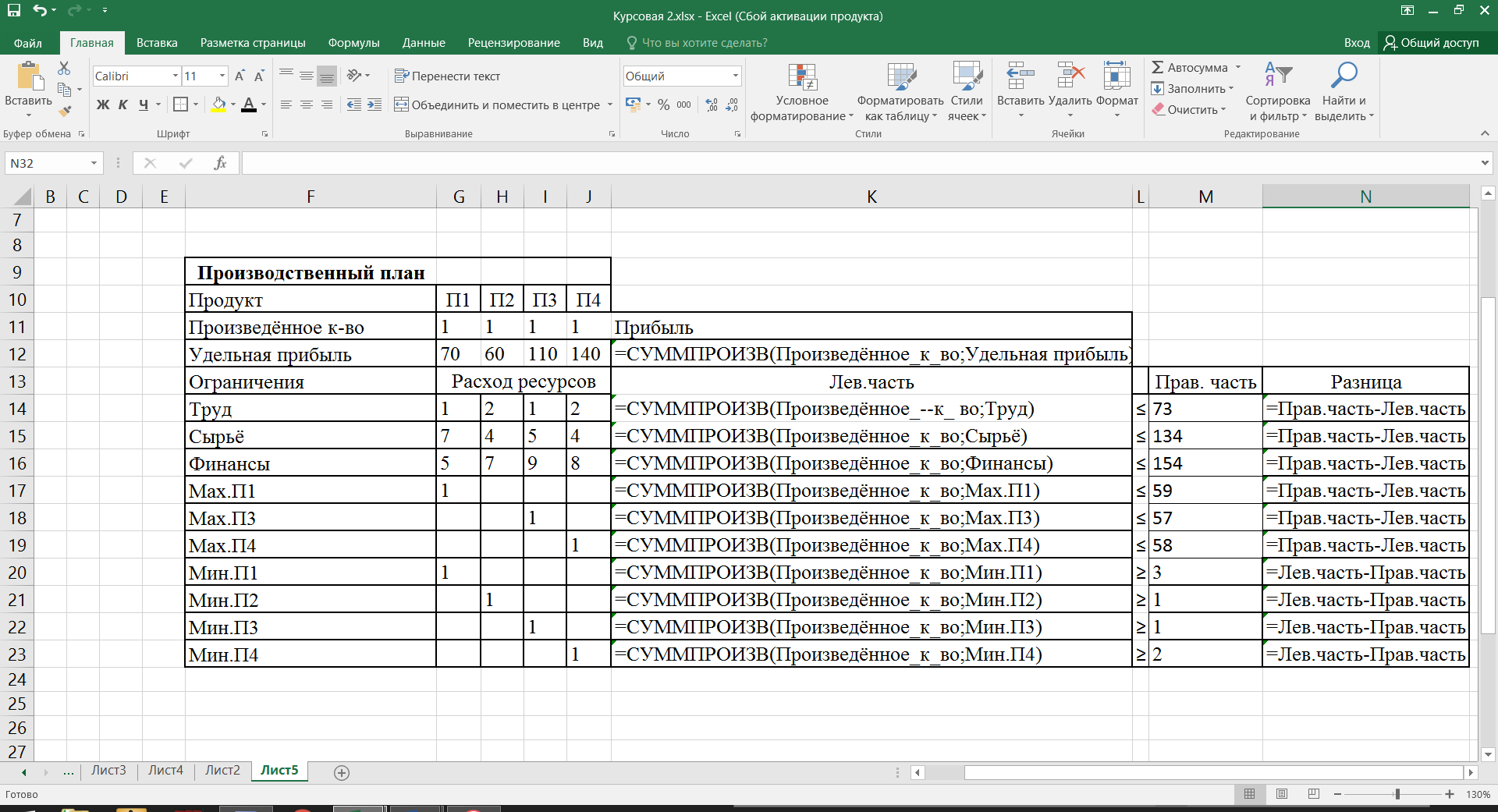 Рис 3. Использование имен диапазонов. 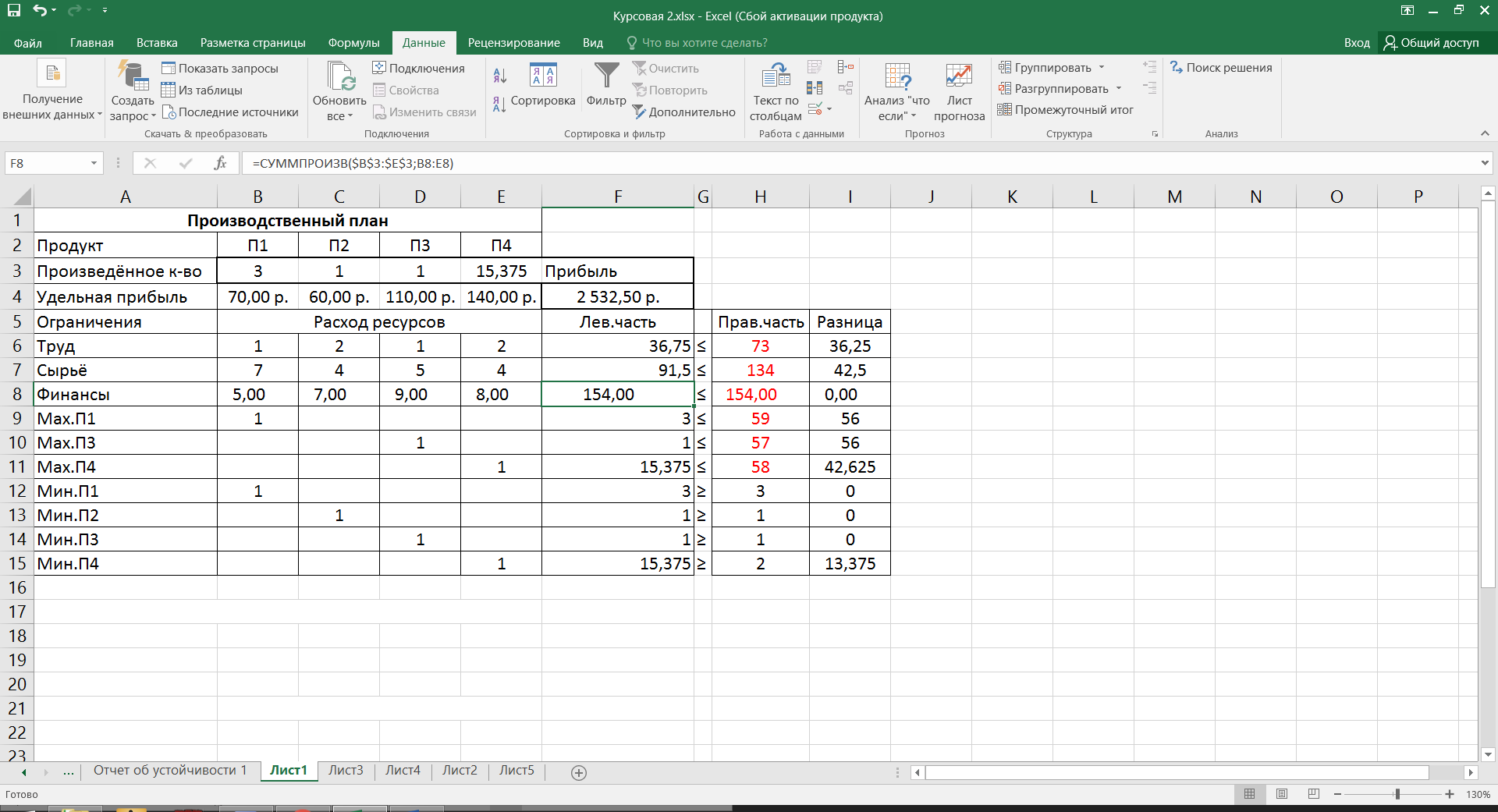 Рис 4. Результаты решения задачи линейного программирования. С) Окно «Поиска решения»:  Рис 4. Окно «Поиска решений»  Рис 5. Окно средства «Поиск решения» Отчёт об устойчивости: 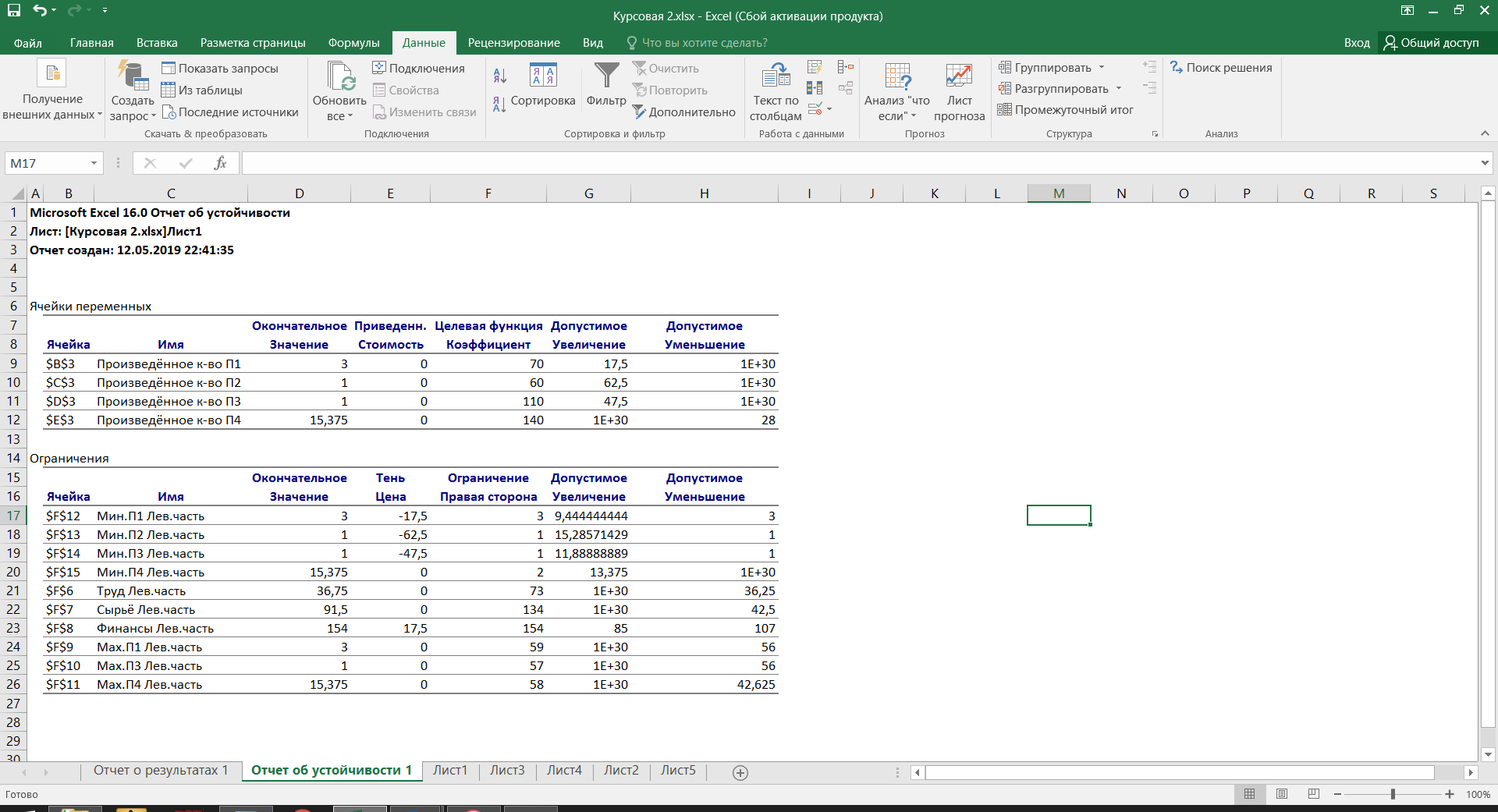 Рис 6. Отчёт об устойчивости Отчёт о результатах: 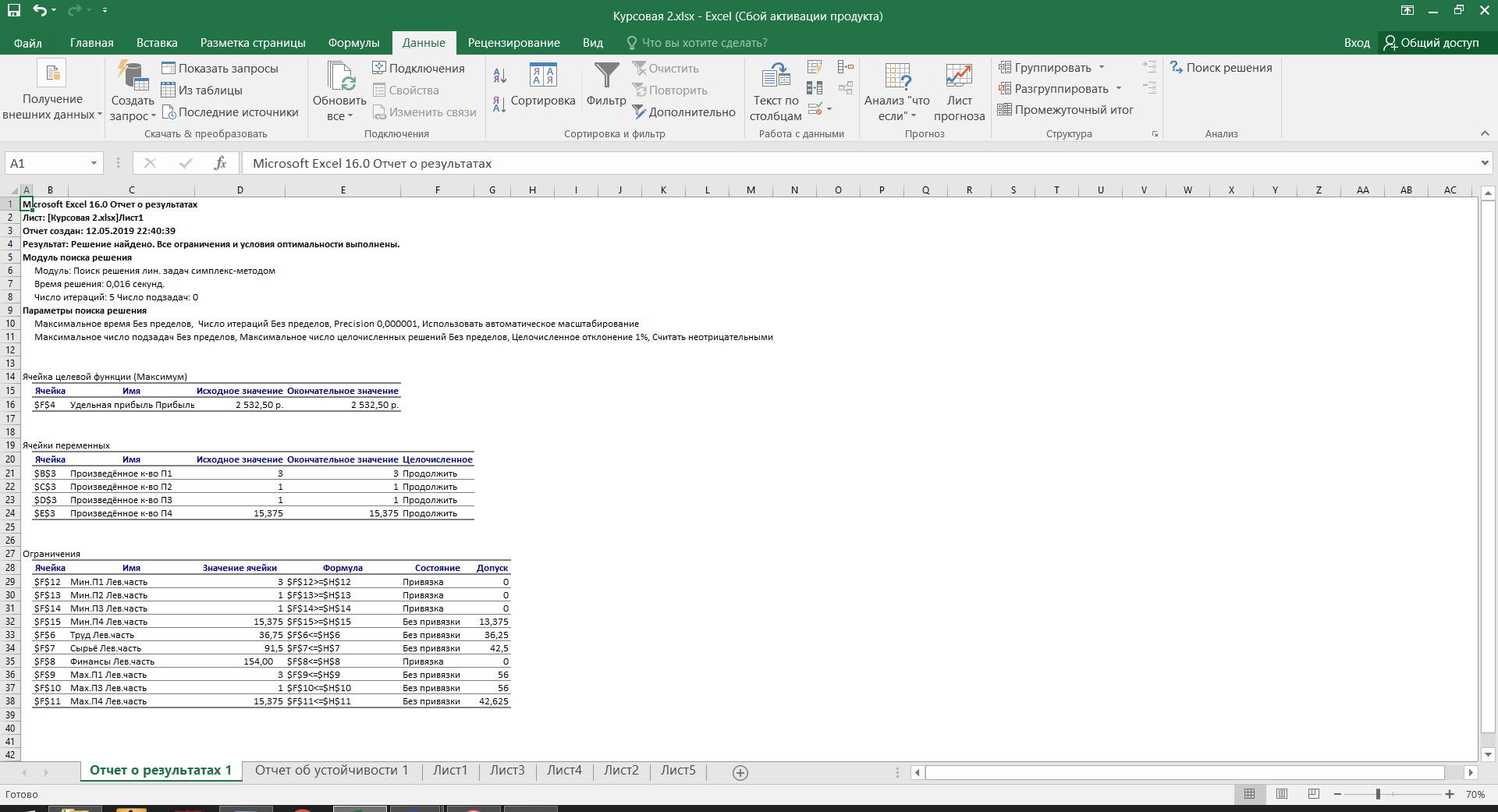 Рис 7. Отчёт о результатах Ответы на вопросы по модели линейного программирования:
Оптимальный производственный план предполагает производство 3 единиц Продукта 1, 1 единицы Продукта 2, 1 единицы Продукта 3, 15,375 единиц Продукта 4. Данный производственный план обеспечит прибыль в размере 2532,50 руб.
Интервалом оптимальности для Продукта 1 является (3,9; 444], для Продукта 2 - (1; 15,285], для Продукта 3 - (1; 11,888], для Продукта 4 – [13,375; 1Е+30).
Дефицитным ресурсом являются финансы, так как их теневая цена отлична от 0.
Финансы можно купить (занять) по цене 17,5 руб. за 1 руб. полученных финансов. Можно приобрести дополнительно 107 руб. финансов. Транспортная задача А) Описание ситуации, обозначения переменных и алгебраическая формулировка: На трех складах завода «Калашников» имеется однородный груз – автоматы АК-12 в количестве 179, 279 и 479 ед., которые необходимо доставить в четыре воинские части в количестве, соответственно 200, 100, 150 и 250 ед. Затраты на безопасную транспортировку 1 автомата АК-12 заданы матрицей, в которой номер строки соответствует номеру склада, а номер столбца – номеру воинской части: 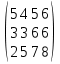 Необходимо составить такой план перевозок, чтобы транспортные расходы завода «Калашников» оказались минимальны. Обозначим объем перевозок с i-го склада в j-ую воинскую часть через 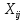 , а целевую функцию (общие затраты) – через F, построим математическую модель задачи: , а целевую функцию (общие затраты) – через F, построим математическую модель задачи:F=5 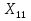 +4 +4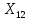 +5 +5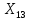 +6 +6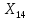 +3 +3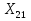 +3 +3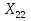 +6 +6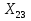 +6 +6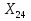 +2 +2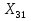 +5 +5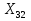 +7 +7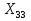 +8 +8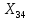 →min →min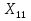 + +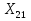 + +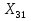 ≥200, ≥200,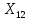 + +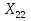 + +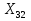 ≥100, ≥100,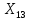 + +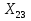 + +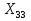 ≥150, ≥150,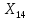 + +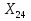 + +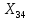 ≥250, ≥250,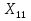 + +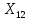 + +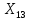 + +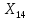 ≤179, ≤179,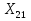 + +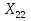 + +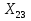 + +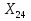 ≤279, ≤279,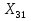 + +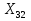 + +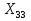 + +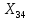 ≤479, ≤479,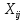 ≥0, где i ≥0, где i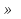 [1;3], j [1;3], j [1;4]. [1;4].B) Табличная модель: 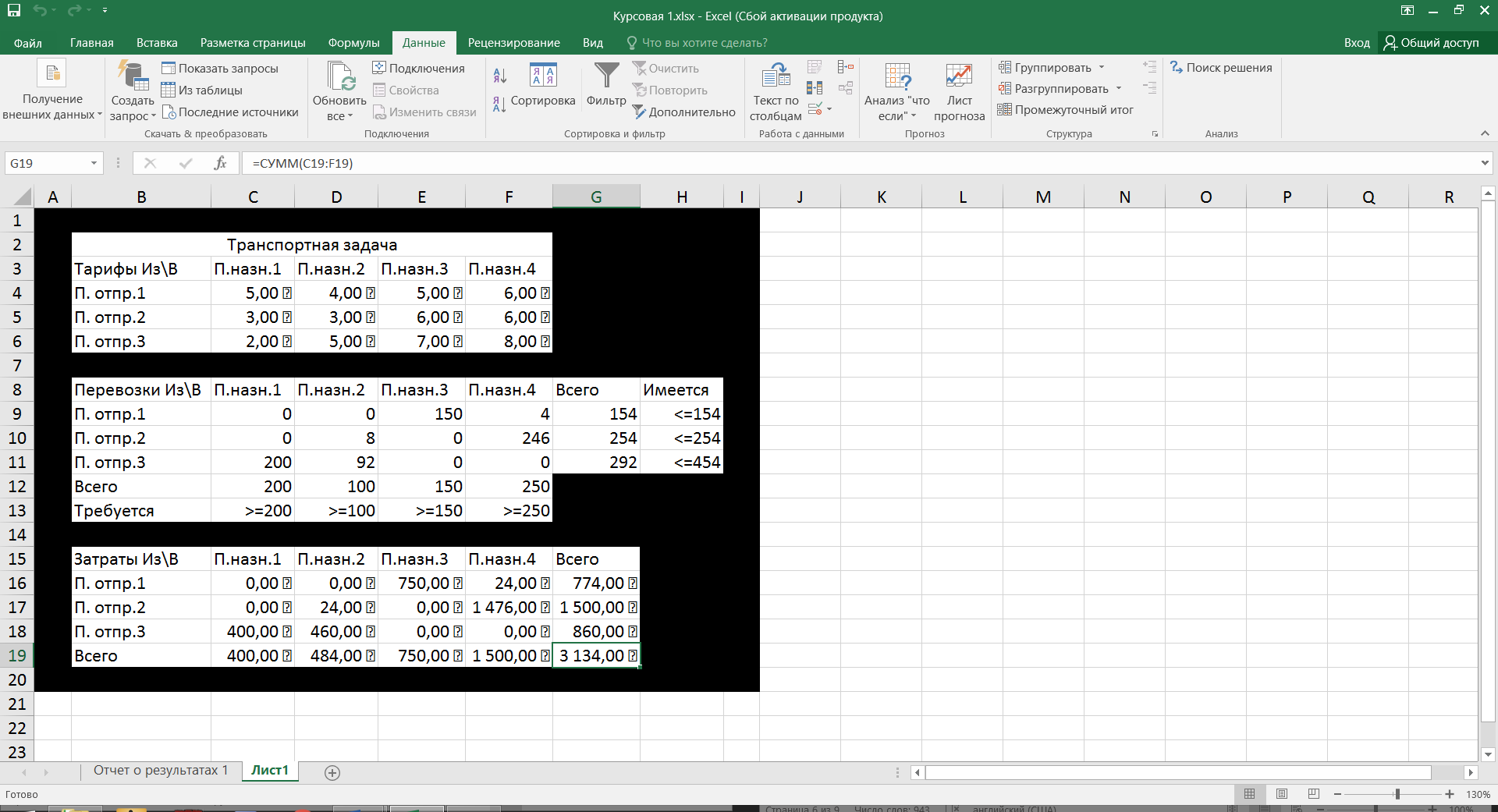 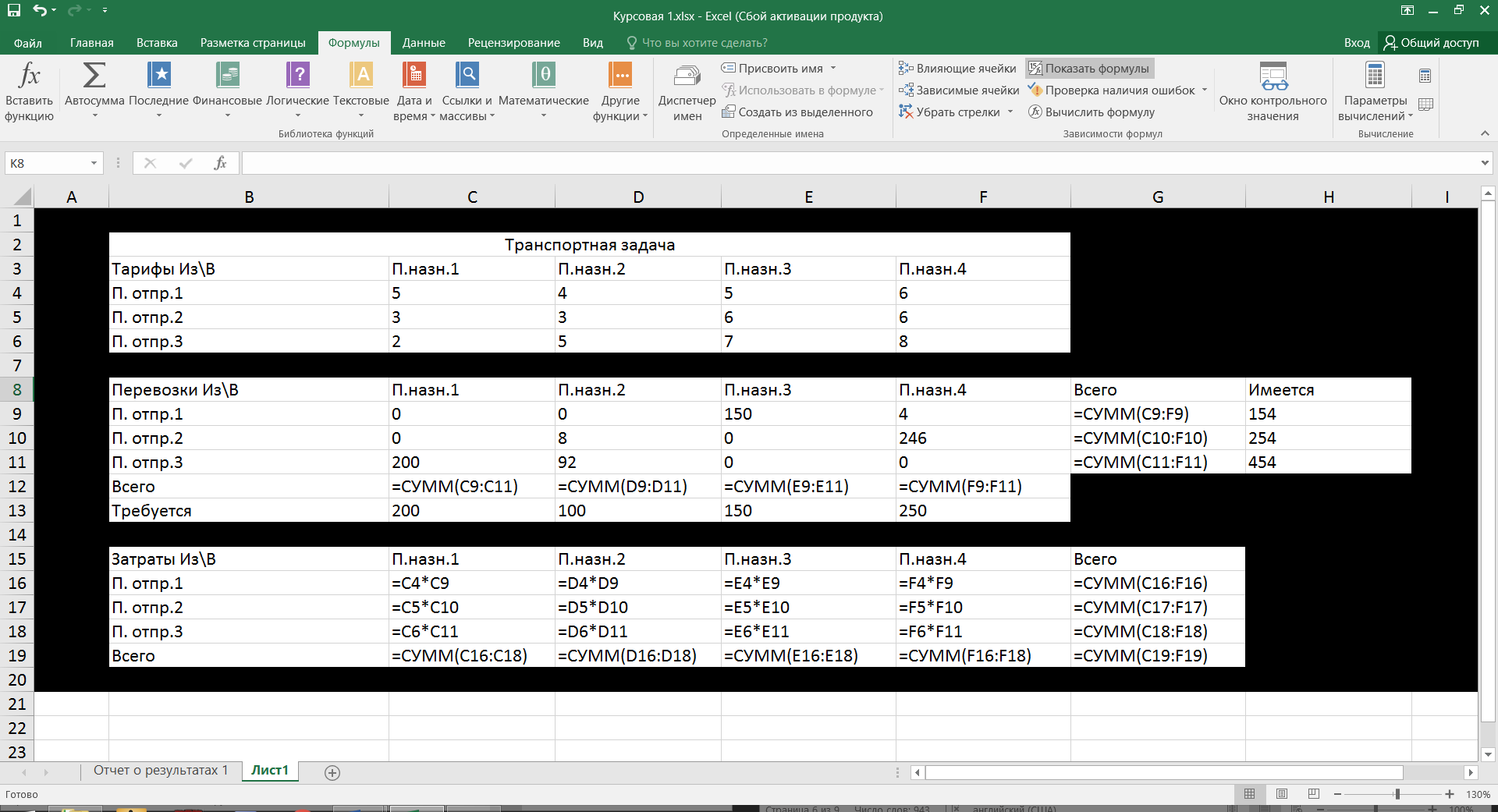 Рис. 7. Транспортная задача на листе Excel C) Окно «Поиска решения»: 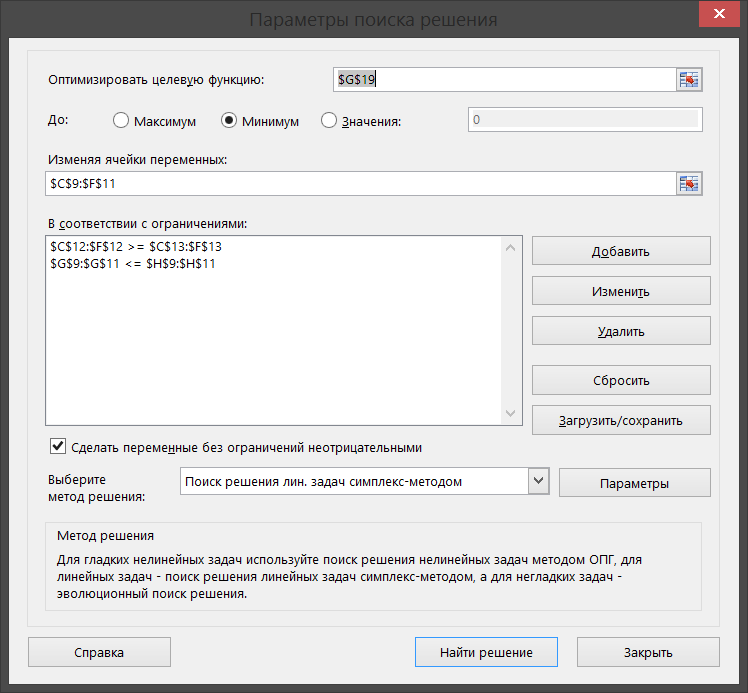 Рис.8. Задание данных для поиска решения транспортной задачи D) Отчет об устойчивости: 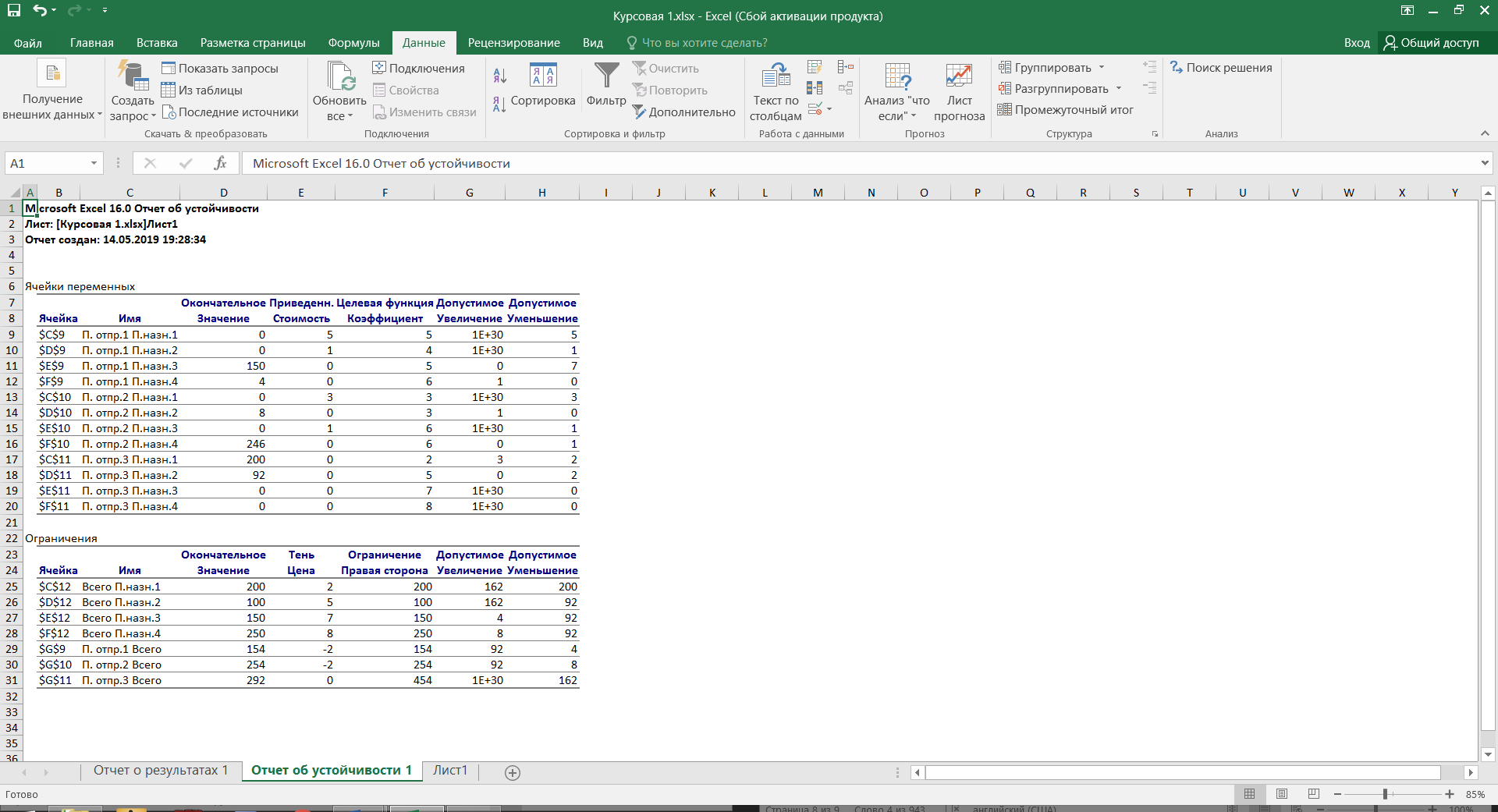
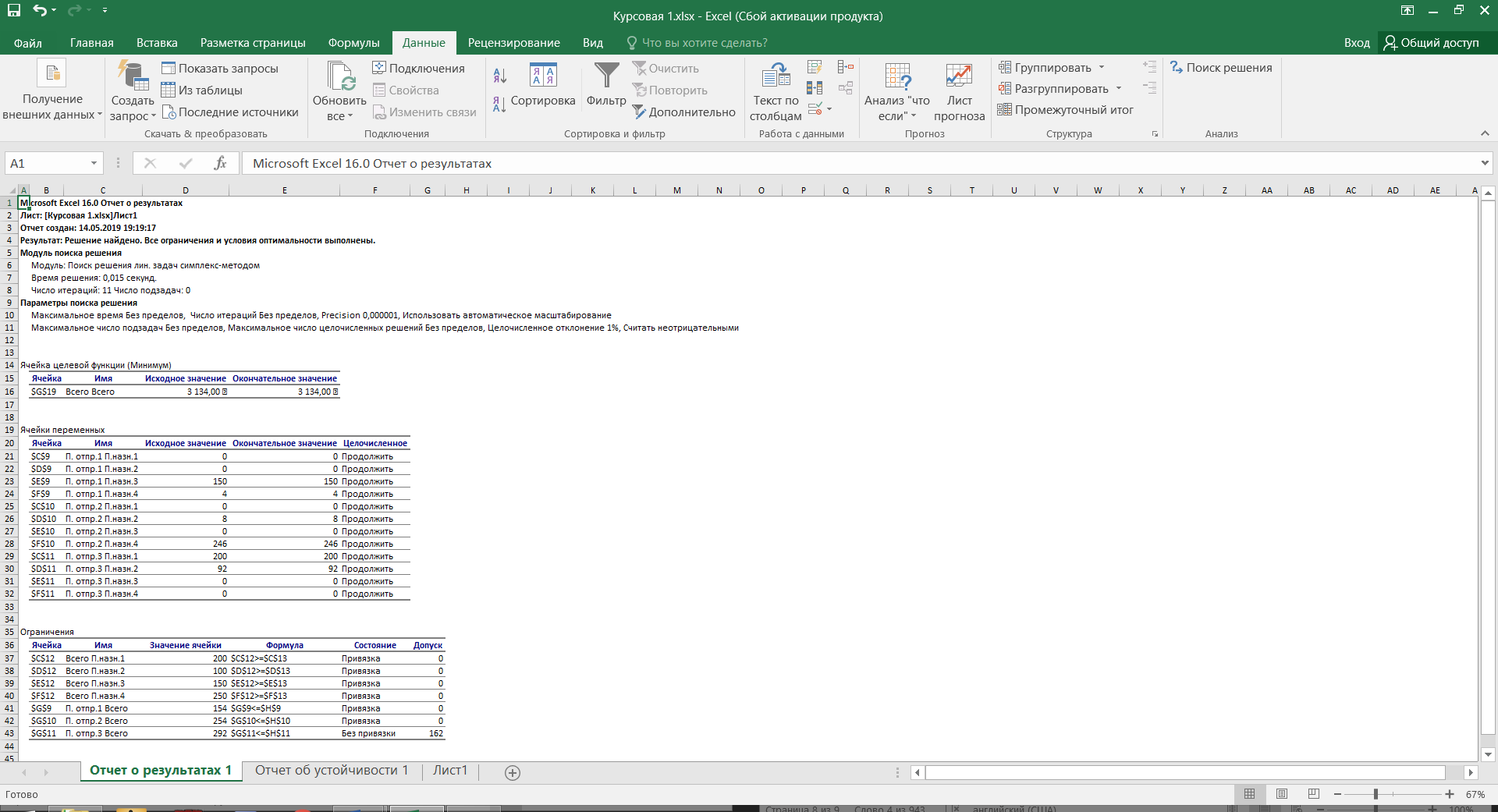 |
