|
|
КР1. Математические основы теории систем, 2002 г
Министерство науки и высшего образования
Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерных систем в управлении и проектировании (КСУП)
Контрольная работа №1
по дисциплине «Математические основы теории систем»
выполнена по методике Карпов А.Г. «Математические основы теории систем, 2002 г.»
Выполнил студент
Группа!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!
25 September 2022 г.
Руководитель работы
_________________/Должность/
_________________Ф.И.О.
_________________/Подпись/
_________________/Дата/
ТОМСК 2022 г
ВОПРОСЫ ПЕРВОЙ ГРУППЫ
Классификация абстрактных моделей
В моделировании есть два различных подхода. Модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Например, это игрушечный кораблик, домик из кубиков, деревянная модель самолета в натуральную величину, используемая в авиаконструировании и др. Модели такого рода называют натурными.
Модель может, однако, отображать реальность более абстрактно – словесным описанием в свободной форме, описанием, формализованным по каким-то правилам, математическими соотношениями и т.п. Будем называть такие модели абстрактными.
Классификация абстрактных моделей:
1. Вербальные(текстовые) модели. Эти модели используют последовательности предложений на формализованных диалектах естественного языка для описания той или иной области действительности (примерами такого рода моделей являются милицейский протокол, правила дорожного движения).
2. Математические модели – очень широкий класс знаковых моделей (основанных на формальных языках над конечными алфавитами), использующих те или иные математические методы. Например, математическая модель звезды будет представлять собой сложную систему уравнений, описывающих физические процессы, происходящие в недрах звезды. Другой математической моделью являются, например, математические соотношения, позволяющие рассчитать оптимальный (наилучший с экономической точки зрения) план работы какого-либо предприятия.
3. Информационные модели – класс знаковых моделей, описывающих информационные процессы (получение, передачу, обработку, хранение и использование информации) в системах самой разнообразной природы. Примерами таких моделей могут служить OSI– семиуровневая модель взаимодействия открытых систем в компьютерных сетях, или машина Тьюринга – универсальная алгоритмическая модель.
Подчеркнем, что граница между вербальными, математическими и информационными моделями может быть проведена весьма условно. Так, информационные модели иногда считают подклассом математических моделей. Однако, в рамках информатики как самостоятельной науки, отделенной от математики, физики, лингвистики и других наук, выделение информационных моделей в отдельный класс является целесообразным.
Отметим, что существуют и иные подходы к классификации абстрактных моделей; общепринятая точка зрения здесь еще не установилась.
В прикладных науках различают следующие виды абстрактных моделей:
1) чисто аналитические математические модели, не использующие компьютерных средств;
2) информационные модели, имеющие приложения в информационных системах;
3) вербальные языковые модели;
4) компьютерные модели, которые могут использоваться для:
• численного математического моделирования;
• визуализации явлений и процессов (как для аналитических, так и для численных моделей);
• специализированных прикладных технологий, использующих компьютер (как правило, в режиме реального времени) в сочетании с измерительной аппаратурой, датчиками и т.п.
Модель состава системы.
Приведите пример:
моделей, имеющих одинаковый элементный состав, но различающихся делением на подсистемы;
моделей, имеющих одинаковые подсистемы, но различающиеся элементным составом;
При рассмотрении модели “чёрного ящика”, мы не касались вопросов внутреннего устройства системы. Для этого нужны более детальные и развитые модели. При внимательном рассмотрении системы можно обнаружить, что она неоднородна и включает в себя множество составных частей. При ещё более внимательном рассмотрении оказывается, что эти составные части также не элементарны и могут быть представлены как набор элементов, и т.д. Части, которые мы считаем неделимыми, называются элементами. Части, состоящие более чем из одного элемента, называются подсистемами. В результате получается модель состава системы, описывающая из каких подсистем и элементов она состоит.
Процесс построения модели состава системы неоднозначен. Этому способствуют следующие факторы:
Понятие элементарности можно определить по разному, в зависимости от цели.
Систему можно разбить на части множеством различных способов. В зависимости от цели, можно получить различные модели состава.
Деление целого на части в определённой степени условно. Границы между подсистемами относительны, это же относится и границам самой системы с окружающей средой.
Приведём примеры двух моделей состава.
Модель A моделирует операционную систему компьютера. Модель B – телевизор. И в той и другой модели можно выделить следующие три подсистемы: подсистема ввода, вывода и преобразования. В операционной системе происходит постоянный процесс ввода информации, при помощи клавиатуры, мыши, и т.д. После получения информация перерабатывается, и передаётся на устройства вывода: монитор, принтер, и т.д. Телевизор также можно представить, как систему трёх подсистем: при помощи панели управления принимаются команды на отображение того или иного канала. Затем эти команды обрабатываются, и нужная программа отображается при помощи кинескопа. Во всех этих случаях функции системы осуществлялись при помощи подсистемы ввода, подсистемы вывода и подсистемы преобразования. Однако элементный состав этих подсистем различен. В первом случае, это: драйвера клавиатуры и мыши, которые принимают поступившие из вне команды; ядро подсистемы ввода-вывода, которое отвечает за преобразование поступивших команд и вывод результата на соответствующие устройства (используя соответствующие драйверы). В модели телевизора, это – интегральные микросхемы, кнопки, транзисторы, резисторы, конденсаторы, лампы и другие радио - элементы. Таким образом, мы получили одинаковые подсистемы, но разный элементный состав.
Теперь рассмотрим модели двух интегральных микросхем. Допустим, в первой из них существуют следующие подсистемы: конвертор, модулятор, усилитель. Другая модель содержит следующие подсистемы: демодулятор, дешифровщик и преобразователь. Ясно, что несмотря на различное деление системы на подсистемы, элементный состав обоих одинаков, в том и другом случае это радио - элементы.
Второе определение системы.
В самом первом приближении систему можно рассмотреть как средство достижения цели. Однако это определение довольно расплывчато и может служить скорее пояснением, чем определением. Второе, более корректное и чёткое определение системы можно дать после рассмотрения трёх видов моделей: “чёрного ящика”, состава и структуры. Объединяя все качественные признаки и свойства этих моделей, можно сказать что система – это совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как единое целое. Графическое изображение такой модели, объединяющей и модель “чёрного ящика”, и модель состава, и модель структуры, называется структурной схемой системы. На структурной схеме указаны все элементы, все связи между элементами и связи определённых элементов с окружающей средой.
Классификация систем по происхождению.
Чтобы иметь возможность сравнивать и различать системы, необходимо иметь их некоторую классификацию. Всякая классификация есть модель реальности, поэтому, в зависимости от цели и задачи, можно строить различные классификации.
Наиболее простой является классификация по происхождению, в соответствии с которой все системы можно подразделить на естественные, искусственные (созданные человеком) и смешанные. Следующий уровень иерархии для всех трёх введённых классов трудно сформулировать чётко. Поэтому, классификация на втором уровне обладает свойством неполноты. Тем не менее, можно выделить следующие подклассы систем:
Искусственные: машины, роботы, инструменты.
Естественные: живые, неживые, социальные, экологические.
Смешанные: биотехнические (живые организмы и технические устройства), эргономические (человек-оператор, машина), автоматизированные, организационные.
5. Виды систем в соответствии с ресурсным обеспечением. Приведите пример системы:
малой и сложной
большой и простой
большой и сложной
Для функционирования системы и её корректного управления, необходимы различные виды ресурсов: материальные, информационные, энергетические. В соответствии со степенью обладания этими ресурсами можно выделить различные классы систем:
Обычные и энергокритичные системы.
Если количество энергии, необходимое для управления объектом мало, по сравнению с энергетическими затратами самого объекта управления, то такие системы называются обычными. Но в некоторых случаях, управляемая и управляющая части могут потреблять соизмеримое количество энергии и питаться от одного источника. В этом случае возникает нетривиальная задача перераспределения ограниченной энергии между этими частями, и мы получаем класс энергокритичных систем.
Большие и малые.
Различные материальные ограничения также порождают два класса систем. Например, в случае управления ЦВМ объектом большой размерности, возникает проблема дефицита оперативной памяти и низкой скорости быстродействия. В соответствии с этим, большие системы можно определить как системы, моделирование которых затруднено в силу их большой размерности. Переход системы из класса больших в класс малых можно осуществить путём наращивания вычислительной базы или декомпозицией многомерной задачи на совокупность задач, меньшей размерности.
3) Простые и сложные.
В зависимости от количества имеющейся информации о системе, можно говорить о её сложности. Если для управления системой достаточно информации, т.е. процесс управления протекает ожидаемым и корректным образом, то систему можно назвать простой. Однако, если в модели системы имеющейся информации недостаточно для успешного управления, то такую систему относят к классу сложных. Для перевода системы из подкласса сложных в подкласс простых можно использовать два различных метода. Первый метод предписывает выяснить и определить причину сложности, получить недостающую информацию и включить её в модель. Второй способ подразумевает смену цели, что неэффективно в технических системах, однако в отношениях между людьми часто является единственным выходом.
Поскольку перечисленные виды ресурсов более или менее не зависимы, то возможны самые различные сочетания между подклассами этой классификации.
Приведём примеры различных систем.
Малая и сложная система.
Рассмотрим систему “Автомобиль” c точки зрения начинающего водителя. Мы получим модель небольшой размерности, так как число управляющих элементов невелико (руль, педали, кнопки). Поэтому данная система принадлежит к классу малых. Однако, если мы забудем включить в эту модель руководство по вождению, т.е. предположим, что водитель не успел научиться искусству авто вождения, то навряд ли он сможет достойным образом использовать эту систему по назначению. Таким образом, отсутствие информации по авто вождению переводит систему “Автомобиль” в класс сложных.
Большая и простая система.
Рассмотрим мост через реку. Допустим, нас интересуют прочностные характеристики этого моста. Построив для этой системы математическую модель в виде разностной схемы, мы получим, в итоге, систему линейных уравнений. Однако, в зависимости от той точности, которую мы хотим достичь, можно получить систему уравнений как средней, так и очень большой размерности. При решении этой системы на ЭВМ можно столкнуться с существенными трудностями, связанными с количеством оперативной памяти и быстродействием компьютера. При всём этом, однако, модель системы содержит всю необходимую информацию для определения однозначного решения, т.е. система относится к классу простых. В то же время, большая размерность получаемой модели, определяет эту систему как большую.
Большая и сложная система.
Если в предыдущем примере предположить, что исследователь недостаточно хорошо знает теорию упругости или теорию пластичности, но тем не менее построил математическую модель моста и пытается что-то определить, то ясно, что для него система будет большой и сложной. Так как недостаток теоретических сведений и исключение из виду важных факторов рано или поздно даст о себе знать.
ВОПРОСЫ ВТОРОЙ ГРУППЫ
Алфавитное и автоматное отображение. Их различие.
Пусть X={x1,…,xm} и Y={y1,…yk} – два произвольных множества, называемые алфавитами. Их элементы будем называть буквами алфавита. Конечную упорядоченную последовательность букв назовём словом в данном алфавите. Обозначим X* и Y* - множества всех слов в алфавитах X и Y соответственно. Тогда произвольное преобразование дискретной информации можно задать как однозначное отображение S множества слов X* в множество Y*. Отображение S называется алфавитным отображением или алфавитным оператором, а алфавиты X и Y – входным и выходным алфавитами оператора S. Каждому входному слову x оператор S сопоставляет выходное слово y. Поэтому для каждого xÎX* существует своё yÎY* такое, что y = S(x). То есть S есть функция, область определения которой X*, а область значений - Y*.
Любой абстрактный автомат реализует некоторый оператор S или индуцирует некоторое отображение S. При появлении на входе автомата некоторого входного слова x на основании функции перехода d: Q ´ X®Q
и функции выхода l: Q ´ X® Y будет сгенерировано выходное слово y. Соотнося каждому входному слову соответствующее ему выходное, получим искомое отображение, которое и является автоматным отображением или автоматным оператором. Если результатом применения оператора к слову x будет выходное слово y, то это обозначается так: S(q1,x) = y или S(x) = y.
Автоматное отображение можно определить индуктивно, для этого нужно определить расширенные функции перехода и выхода, распространив их область определения на всё множество входных слов X*:
d(qi, xj) задано первоначально,
d(qi, x, xj) = d(d(qi, x), xj),
l(qi, x, xj) = l(d(qi, x), xj).
Тогда, автоматное отображение S можно определить следующим образом:
a) S(qi, xj) = l(qi, xj)
b) S(qi, x, xj) = S(qi, x) l(d(qi, x), xj)
Различие между алфавитным и автоматным отображением заключается в том, что во втором случае для определения выходного слова необходимо знать текущее состояние автомата qi. Причём генерация выходного слова происходит при помощи двух функций автомата: перехода d и выхода l. Таким образом, автоматный оператор является отображением: Q ´ X®Y.
Понятие изоморфизма и эквивалентности автоматов.
Пусть S = S, QS, YS, dS, lS> и T = T, QT, YT, dT, lT> есть два автомата. Три отображения f: XS®XT, g: QS®QT и h: YS®YT называются гомоморфизмом автомата S в автомат T, если для любых xÎXS, qÎQS, и yÎYS выполняются условия:
dT(g(q) ,f(x)) = g(dS(q, x)),
lT(g(q), f(x)) = h(lS(q, x)).
В этом случае автомат T называется гомоморфным автомату S. Если все три отображения сюрьективны, то эта тройка называется гомоморфизмом S на T. Если, кроме того, эти отображения взаимно однозначны, то они называются изоморфизмом S на T. Автоматы, для которых существует изоморфизм, называются изоморфными. Этот факт обозначается так: ST.
Пусть оба автомата S и T имеют одинаковые входные и выходные алфавиты. Состояние q автомата S и состояние r автомата T называют неотличимыми, если для любого входного слова S(q,x) = T(r,x). Автоматы S и T называют неотличимыми, если для любого состояния q автомата S найдётся неотличимое от него состояние r автомата T и наоборот. Отношение неотличимости между состояниями (и автоматами) рефлексивно, симметрично и транзитивно, а, следовательно, является отношением эквивалентности. Это и явилось основанием называть неотличимость эквивалентностью и говорить об эквивалентных состояниях или эквивалентных автоматах, имея ввиду отношение неотличимости. Переход от автомата S к эквивалентному ему автомату называется эквивалентны преобразованием автомата S.
Представление событий автоматами.
Пусть X={x1,…,xm} произвольный входной алфавит, а X* - множество всех слов в этом алфавите. Тогда любое подмножество EÍX* называется событием в алфавите X. Далее будем рассматривать автоматы без выходов.
Событие E называется представимым в автомате S = 1, F>, если d(q1, x)ÎF тогда и только тогда, когда xÎE. Всякому автомату при данных q1 и F однозначно соответствует представимое в нём событие: на графе автомата оно соответствует множеству путей, ведущих из q1 в вершины, принадлежащие множеству заключительных состояний F. Событие называется представимым, если существует конечный автомат, в котором оно представимо. Синонимом этого понятия является: множество определимое или допустимое, или распознаваемое автоматом. Другими словами представимое в автомате событие можно назвать множеством, разрешимым автоматом.
Оказывается, что не все события представимы в автоматах. Об этом говорит следующая
Теорема. Существуют события, не представимые в автоматах, а именно: никакая непериодическая бесконечная последовательность не распознаваема конечным автоматом.
Из этой теоремы следует, что класс множеств, распознаваемых автоматом, есть лишь часть (собственное подмножество) класса разрешимых множеств. Отсюда и из теоремы Райса вытекает, что свойство множества “быть представимым в конечном автомате” алгоритмически неразрешимо.
Понятие регулярного события
Определим три операции над событиями R и S в алфавите X.
Объединением (дизъюнкцией) событий R и S называется событие P, обозначаемое P = RÈS, которое образуется обычным теоретико-множественным объединением множеств R и S.
Умножением (конкатенацией) событий R и S будет событие U =R×S, состоящее из слов вида: u = r×s, где uÎU, rÎR, sÎS, то есть слова события U образуются приписыванием справа любого слова события S к любому слову события R.
Итерацией события R называется событие R* = eÈRÈRRÈRRRÈ…ÈRn… = 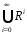 . .
Одноэлементные события, т.е. события {xi}, где xiÎX, называются элементарными и обозначаются буквами xi. Событие e, образованное пустым словом e, состоит из одного слова нулевой длины и также относится к элементарным.
Событие называется регулярным, если оно может быть получено из элементарных событий путём конечного применения операций: объединение, умножение и итерация, которые также называются регулярными.
Понятие источника
Источник (переходный граф сигналов, сигнальный граф) – это ориентированный граф, в котором выделены начальные и заключительные вершины, и на каждом ребре написана буква из алфавита X, либо e – пустое ребро. Каждый источник H однозначно определяет некоторое событие E в алфавите X, порождаемое множеством путей из начальных вершин в заключительные. Источники, представляющие одно и то же событие, называются эквивалентными. Частный случай источника – автомат без выхода.
Для любого источника H можно построить эквивалентный источник H0 с двумя полюсами (с одной начальной вершиной и одной заключительной). Для такого построения нужно в H0 ввести новую вершину q0 (единственная начальная вершина) и соединить её пустыми рёбрами с прежними начальными вершинами в H, а также новую вершину qz (единственную заключительную) и соединить с ней все заключительные вершины в H пустыми рёбрами. В остальном H0 совпадает с H. |
|
|
 Скачать 37.79 Kb.
Скачать 37.79 Kb.
 .
.