108. Материальная точка движется в плоскости хусогласно уравнениям х=A1+B1t+C1t2и y=A2+B2t+C2t2, где B1=7 м/с, С1=– 2м/с2, B2= – 1м/с, С2 =0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t = 5с.
х=A1+B1t+C1t2
y=A2+B2t+C2t2
B1=7 м/с
С1=– 2м/с2
B2= – 1м/с
С2 =0,2 м/с2
t = 5с
|
Запишем радиус-вектор. Он равен 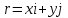 , где i – орт оси X, а j – орт оси Y. Поэтому получаем , где i – орт оси X, а j – орт оси Y. Поэтому получаем 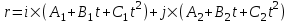 . .
Скорость есть производная перемещения по времени. Поэтому 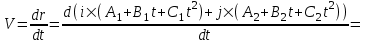
= 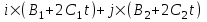 . .
Эта величина является вектором. Проекция скорости V на ось X равна Vx=B1+2C1t, на ось Y равна Vy= B2+2C2t. Тогда модуль скорости равен
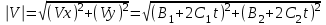 . .
Подставляем числа.
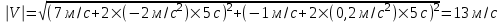 . .
По определению ускорение это производная скорости по времени. Поэтому 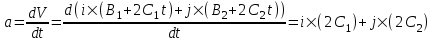 . .
Проекция ускорения a на ось X равна ax=2C1, на ось Y равна ay= 2C2.
Поэтому 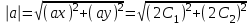 . .
Подставляем числа.
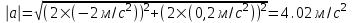 . .
|
V(t) = ?
a(t) = ?
|
129. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью V1 = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью V2 = 580 м/с. С какой скоростью откатилось при этом орудие?
V1= 600 м/с
V2= 580 м/с
|
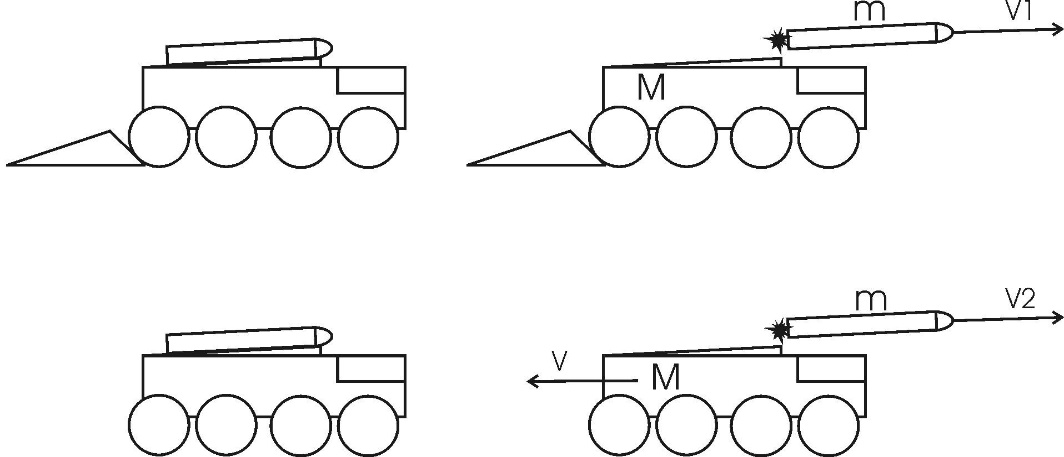
Из закона сохранения импульса получаем, что импульс снаряда во втором случае равен импульсу установки: 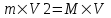 . Откуда искомая скорость равна . Откуда искомая скорость равна 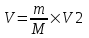 . .
Из закона сохранения энергии получаем, что кинетическая энергия установки равна разности кинетических энергий снаряда в первом и втором случае: 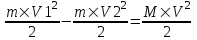 . Откуда . Откуда 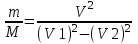 . Подставляем в . Подставляем в 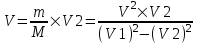 . Откуда . Откуда 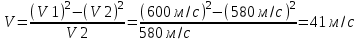 . .
|
V = ?
|
132. Из шахты глубиной H=600 м поднимают клеть массой m1 = 3,0 т на канате, каждый метр которого имеет массу m2= 1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия η подъемного устройства?
H=600 м
m1 = 3,0 т
m2= 1,5 кг
L = 1м
|
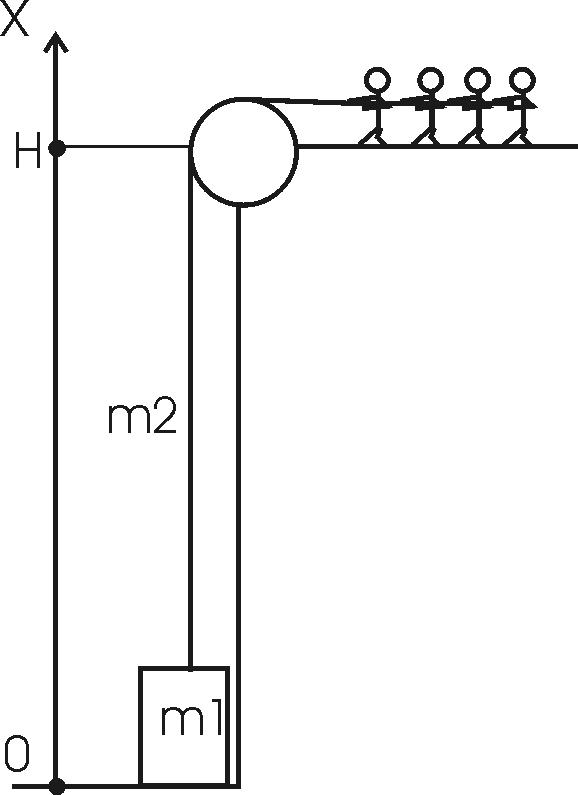
Работа, по определению равна 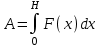 , где F(x) – сила. , где F(x) – сила.
В нашем случае 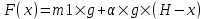 , где m1×g – вес клети, , где m1×g – вес клети, 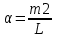 - линейная плотность каната. (При поднимании длина троса уменьшается по закону H–x и, поэтому масса, которая свисает, равна α×(H–x)). - линейная плотность каната. (При поднимании длина троса уменьшается по закону H–x и, поэтому масса, которая свисает, равна α×(H–x)). Тогда 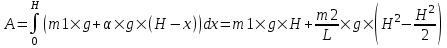 . . Упрощаем 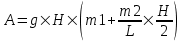 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ). 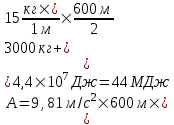 . .
Это совершенная работа, а полезная равна энергии необходимой только на поднятие одной клети: E=m1×g×H.
Поэтому кпд равно 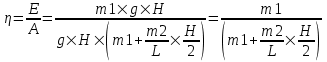 . .
Подставляем числа. 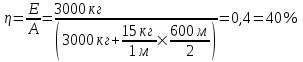 . .
|
A = ?
η = ?
|
150. К концам легкой и нерастяжимой нити, перекинутой через блок, подвешены грузы массами m1 = = 0,2 кг и m2 = 0,3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0,4 кг, а его ось движется вертикально вверх с ускорением а’ = 2 м/с2? Силами трения и проскальзывания нити по блоку пренебречь.
m1=0,2кг
m2=0,3кг
m = 0,4 кг
а’= 2 м/с2
|
В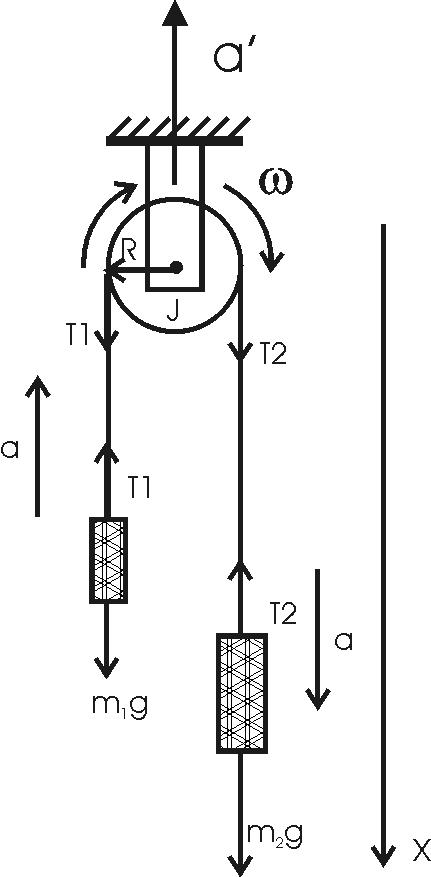 еса первой и второй гири равны P1=m1×g и P2=m2×g соответственно. еса первой и второй гири равны P1=m1×g и P2=m2×g соответственно.
Ввиду того, что масса нити пренебрежимо мала, изменения натяжений T1 и T2 вдоль нити можно не учитывать. Используем второй закон Ньютона и, одновременно проецируем силы на ось X. Тогда уравнения движения грузов и блока будут:
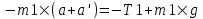 (1) (1)
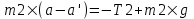 (2) (2)
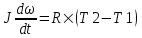 (3) , где J – момент инерции блока. Известно, что для однородного диска массой m и радиусом R момент инерции равен: (3) , где J – момент инерции блока. Известно, что для однородного диска массой m и радиусом R момент инерции равен: 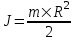 . .
Если проскальзывания нити по блоку нет, то 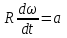 , где a – ускорение грузов, , где a – ускорение грузов, 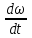 - угловое ускорение блока. Тогда - угловое ускорение блока. Тогда 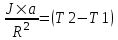 . Из (1) и (2) уравнений находим . Из (1) и (2) уравнений находим
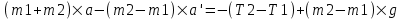 . Подставляем . Подставляем 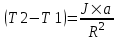 и получаем и получаем 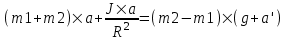 , откуда ускорение равно , откуда ускорение равно 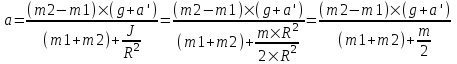 . .
Подставляем ускорение в (1) и находим T1:
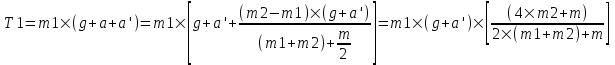 . .
Подставляем ускорение в (2) и находим T2:
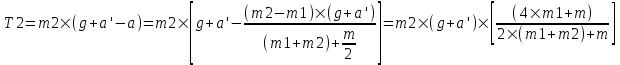 . .
Отношение 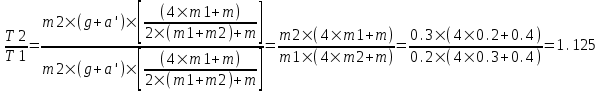 . .
|
T2/T1 = ?
|
152. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω = 4 рад/с. С какой угловой скоростью ω1 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J=5 кг×м2. Длина стержня L=1.8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
ω = 4 рад/с
J = 5 кг×м2
L = 1.8 м
m = 6 кг
|
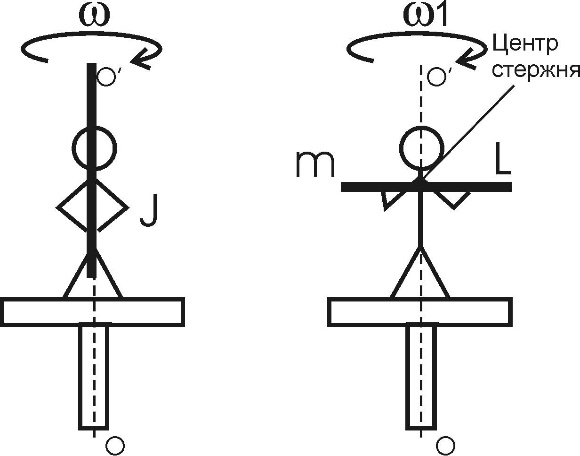
Воспользуемся законом сохранения момента импульса: 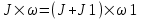 где J – момент импульса человека и скамьи, J1 – момент инерции стержня относительно оси OO’, ω1 – искомая частота вращения. где J – момент импульса человека и скамьи, J1 – момент инерции стержня относительно оси OO’, ω1 – искомая частота вращения.
Момент инерции тонкого стержня массой m и длинной L относительно его центра равен 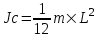 . .
Тогда 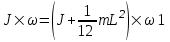 , откуда искомая частота , откуда искомая частота 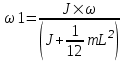 . Подставляем числа. . Подставляем числа. 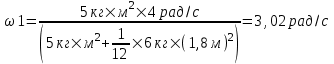 . .
|
ω1 = ?
|
162. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m = 2 кг: 1) с высоты h = 1000 км; 2) из бесконечности?
h1=R=1000км
h2 = ∞
m=2кг
M=6×1024 кг
|
На тело действует сила всемирного тяготения со стороны Земли, равная 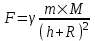 , где , где 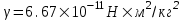 - гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли. - гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли.
Рассмотрим первый случай: h=1000км. Работа по определению равна 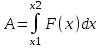 , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), 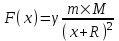 , а x – это положение (высота) тела. Тогда , а x – это положение (высота) тела. Тогда
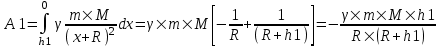 . Подставляем числа. . Подставляем числа. 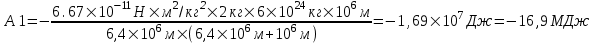 . .
Рассмотрим второй случай: h=∞.
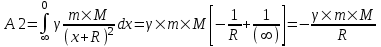 . .
Подставляем числа.
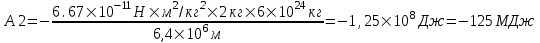 . .
|
A1 = ?
A2 = ?
|
172. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A1×sinω1×t и у=А2×cosω2×t, где A1 = 8 см, A2=4 см, ω1 = ω2=2с-1. Написать уравнение траектории и построить ее. Показать направление движения точки.
x=8sin2t см
y=4cos2t см
|
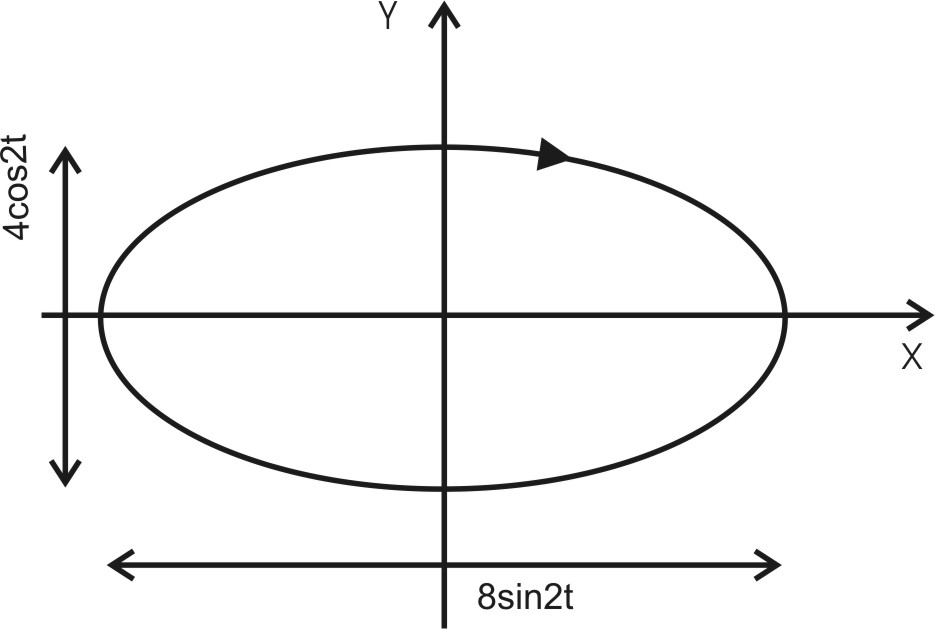
Видно, что 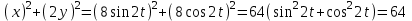 . .
Уравнение 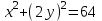 - это эллипс. По другому его записывают в виде - это эллипс. По другому его записывают в виде 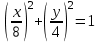 . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем: . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем:
x(t=0)=0см, а y(t=0)=4см. То есть точка находится на оси Y.
В момент t=π/2 получаем:
x(t= π/4)=8см, а y(t= π/4)=0см. То есть точка находится на оси X. Из этого делаем вывод, что точка движется от оси Y к оси X, то есть по часовой стрелке.
|
Траектория - ?
| |
 Скачать 272.81 Kb.
Скачать 272.81 Kb.
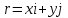 , где i – орт оси X, а j – орт оси Y. Поэтому получаем
, где i – орт оси X, а j – орт оси Y. Поэтому получаем 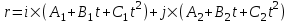 .
.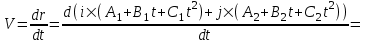
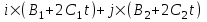 .
.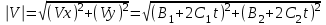 .
.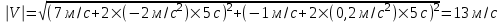 .
.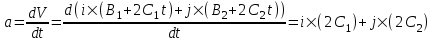 .
. 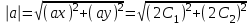 .
. 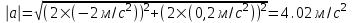 .
.
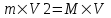 . Откуда искомая скорость равна
. Откуда искомая скорость равна 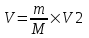 .
.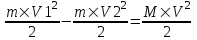 . Откуда
. Откуда 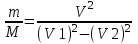 . Подставляем в
. Подставляем в 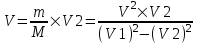 . Откуда
. Откуда 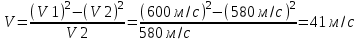 .
.
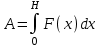 , где F(x) – сила.
, где F(x) – сила.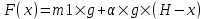 , где m1×g – вес клети,
, где m1×g – вес клети, 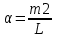 - линейная плотность каната. (При поднимании длина троса уменьшается по закону H–x и, поэтому масса, которая свисает, равна α×(H–x)).
- линейная плотность каната. (При поднимании длина троса уменьшается по закону H–x и, поэтому масса, которая свисает, равна α×(H–x)). 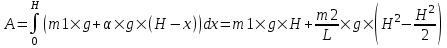 .
.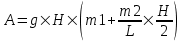 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ). 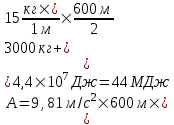 .
. 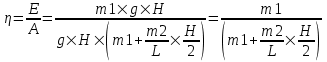 .
.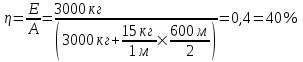 .
. еса первой и второй гири равны P1=m1×g и P2=m2×g соответственно.
еса первой и второй гири равны P1=m1×g и P2=m2×g соответственно. 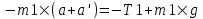 (1)
(1)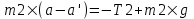 (2)
(2)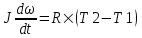 (3) , где J – момент инерции блока. Известно, что для однородного диска массой m и радиусом R момент инерции равен:
(3) , где J – момент инерции блока. Известно, что для однородного диска массой m и радиусом R момент инерции равен: 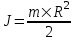 .
.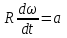 , где a – ускорение грузов,
, где a – ускорение грузов, 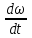 - угловое ускорение блока. Тогда
- угловое ускорение блока. Тогда 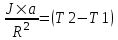 . Из (1) и (2) уравнений находим
. Из (1) и (2) уравнений находим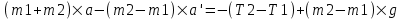 . Подставляем
. Подставляем 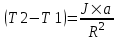 и получаем
и получаем 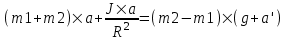 , откуда ускорение равно
, откуда ускорение равно 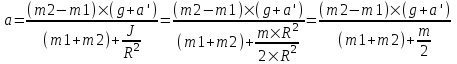 .
. 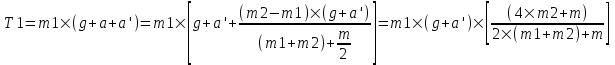 .
. 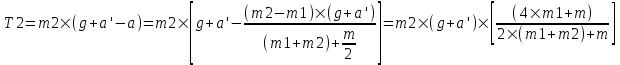 .
.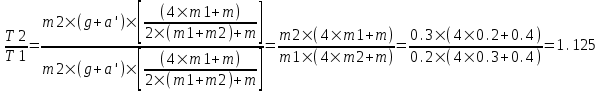 .
.
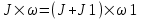 где J – момент импульса человека и скамьи, J1 – момент инерции стержня относительно оси OO’, ω1 – искомая частота вращения.
где J – момент импульса человека и скамьи, J1 – момент инерции стержня относительно оси OO’, ω1 – искомая частота вращения. 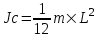 .
. 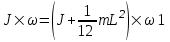 , откуда искомая частота
, откуда искомая частота 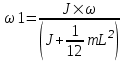 . Подставляем числа.
. Подставляем числа. 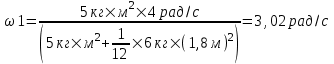 .
.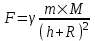 , где
, где 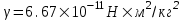 - гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли.
- гравитационная постоянная, M – масса Земли, R – это радиус Земли, h – расстояние от тела до поверхности Земли.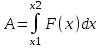 , где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0),
, где x1 – начальное положение тела (x1=R), x2 – конечное (x2=0), 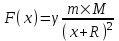 , а x – это положение (высота) тела. Тогда
, а x – это положение (высота) тела. Тогда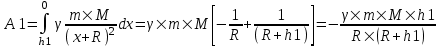 . Подставляем числа.
. Подставляем числа. 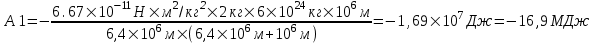 .
.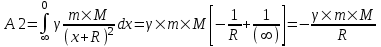 .
.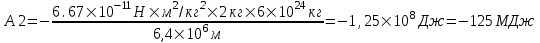 .
.
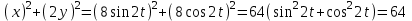 .
.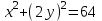 - это эллипс. По другому его записывают в виде
- это эллипс. По другому его записывают в виде 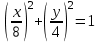 . Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем:
. Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория – эллипс. Теперь найдем направление движения. В момент t=0 получаем: