физика. коллоквиум ФОМТ. Механические характеристики современной бормашины
 Скачать 0.99 Mb.
|
Механические характеристики современной бормашины.
2. Кинематика точки. Скорость и ускорение точки, их направление. См. документ. 3. Вращательное движение. Кинематические уравнения равномерного и равнопеременного вращательного движения. См.документ. Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими at и an. Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек2). Закон вращательного движения тела выражается уравнением φ = f (t). Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени ω = dφ/dt = f' (t). Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости ε = dω/dt = f'' (t). Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φоб. Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот. Так как один полный оборот соответствует 2π рад, то φ = 2πφоб и φоб = φ/(2π). Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин. Переход от одних единиц угловой скорости к другим производится по формулам ω = πn/30 и n = 30ω/π. Рис. 205. Вращательное движение тела При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, at и an, характеризующими движение различных точек этого тела (рис 205). Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так: s = φR. Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством v = ωR. Касательное ускорение точки зависит от углового ускорения и определяется формулой at = εR. Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью an = ω2R. При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение. Равномерное вращательное движение Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения имеет вид φ = φ0 + ωt. В частном случае, когда начальный угол поворота φ0=0, φ = ωt. Угловую скорость равномерно вращающегося тела ω = φ/t можно выразить и так: ω = 2π/T, где T – период вращения тела; φ=2π – угол поворота за один период. Равнопеременное вращательное движение Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения. Уравнение равнопеременного вращения (1)φ = φ0 + ω0t + εt2/2 и уравнение, выражающее угловую скорость тела в любой момент времени, (2)ω = ω0 + εt представляют совокупность основных формул вращательного равнопеременного движения тела. В эти формулы входят всего шесть величин: три постоянных для данной задачи φ0, ω0 и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин. Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы. Исключим из (1) и (2) угловое ускорение ε: (3)φ = φ0 + (ω + ω0)t/2. Исключим из (1) и (2) время t: (4)φ = φ0 + (ω2 - ω02)/(2ε). В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ0=0 и ω0=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид: (5)φ = εt2/2; (6)ω = εt; (7)φ = ωt/2; (8)φ = ω2/(2ε). 4. Вращательное движение, момент инерции твердого тела, теорема Гюйгенса – Штейнера https://zaochnik.ru/blog/moment-inercii-dlya-chajnikov-opredelenie-formuly-primery-resheniya-zadach/ Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси. При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения. Момент инерции твердого тела - это величина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении. Формула момента инерции: Единица момента инерции - килограмм-метр в квадрате. Теорема Штейнера: Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями. Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции телаотносительно некоторой оси.  5. Дайте определение момента силы относительно неподвижной оси z , кинетической энергии вращения. Сформулируйте основной закон (уравнение динамики ) вращательного движения. См. презентацию 6. Дайте определение момента импульса относительно неподвижной оси z. Сформулируйте закон сохранения момента импульса. См. документ 7. Центрифугирование. Центростремительная сила при центрифугировании. См. ответы 8. Что называется силой сухого трения? Какими видами сил представлена сила сухого трения? Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения: трение скольжения, трение покоя, трение качения. 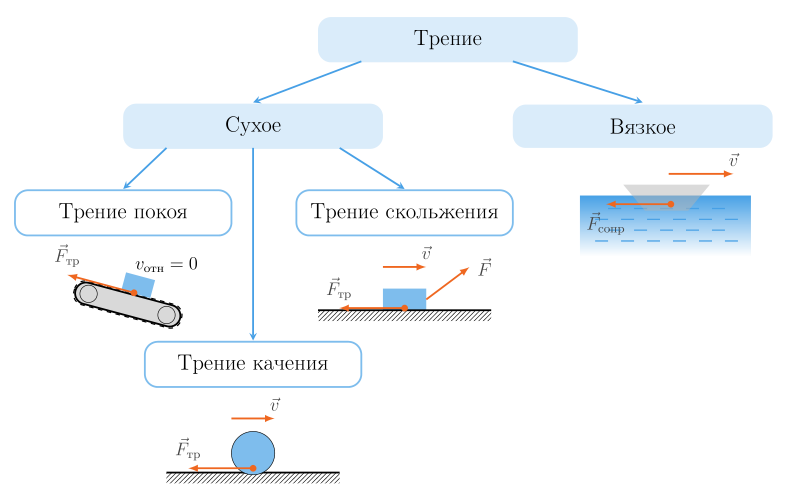 https://externat.foxford.ru/polezno-znat/wiki-fizika-sily-treniya 9. Нарисуйте схемы действия сил на движущиеся тела в которых присутствуют силы сухого трения. https://uchitel.pro/трение-покоя-и-трение-скольжения/#::text=Сила%20трения%20скольжения%20возникает%20при,опоры%3B%20μ%20–%20коэффициент%20трения 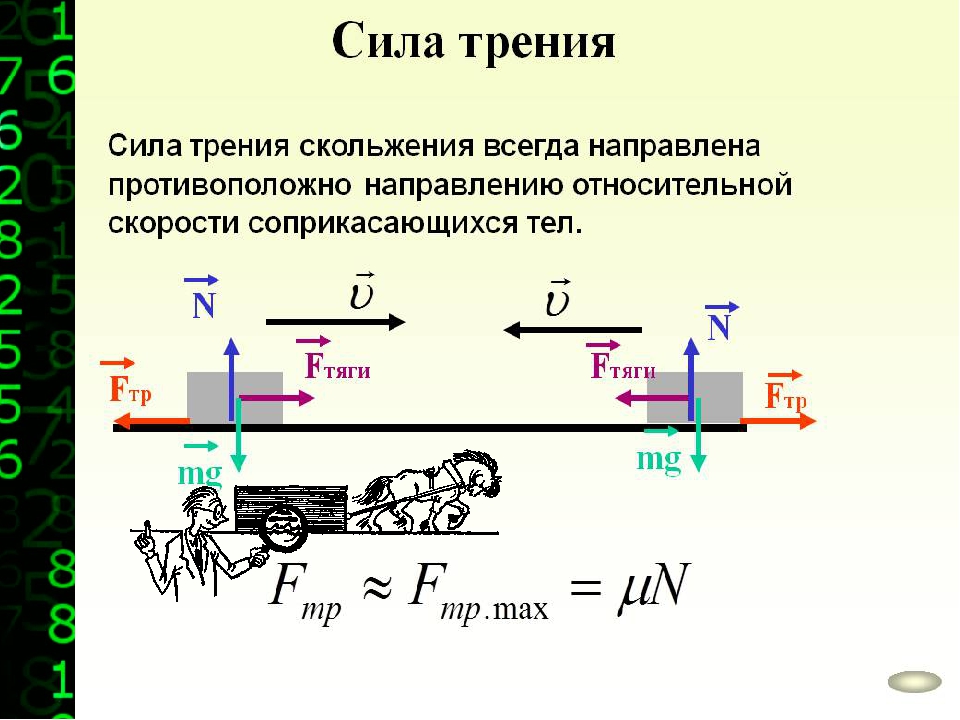 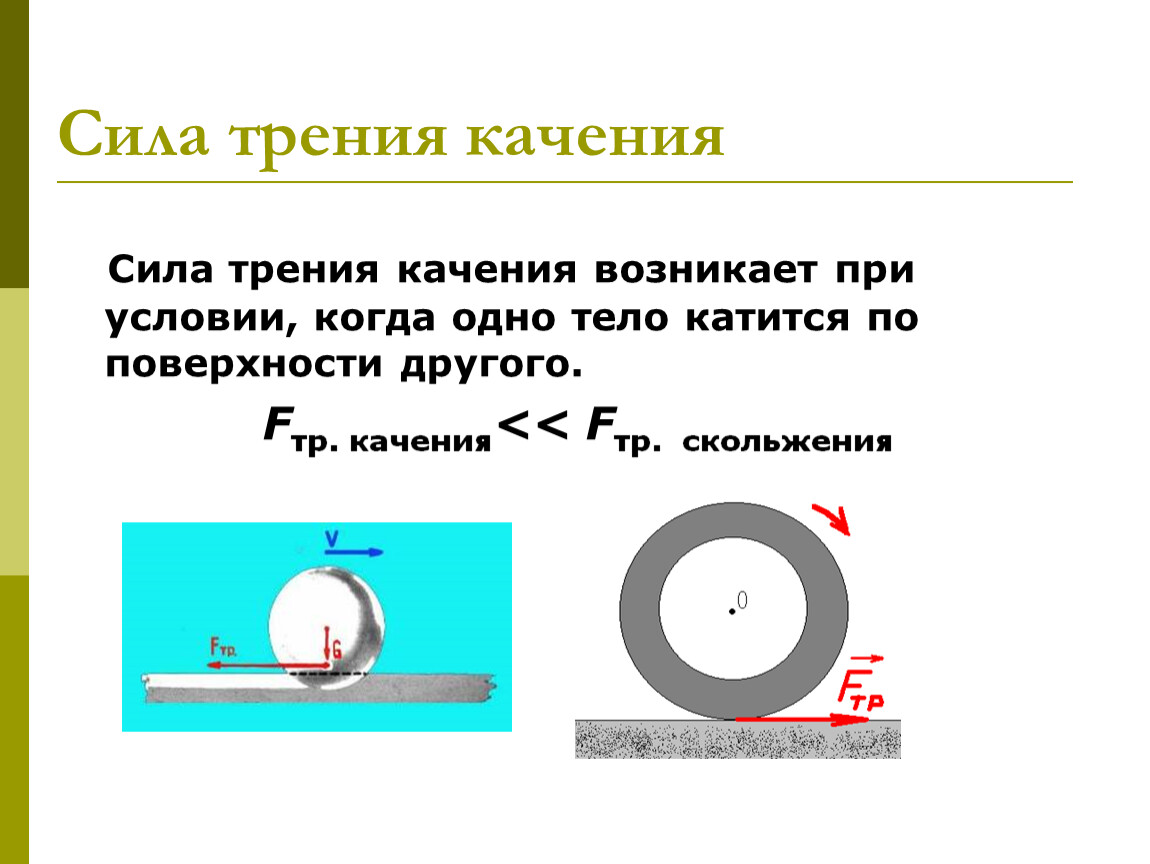 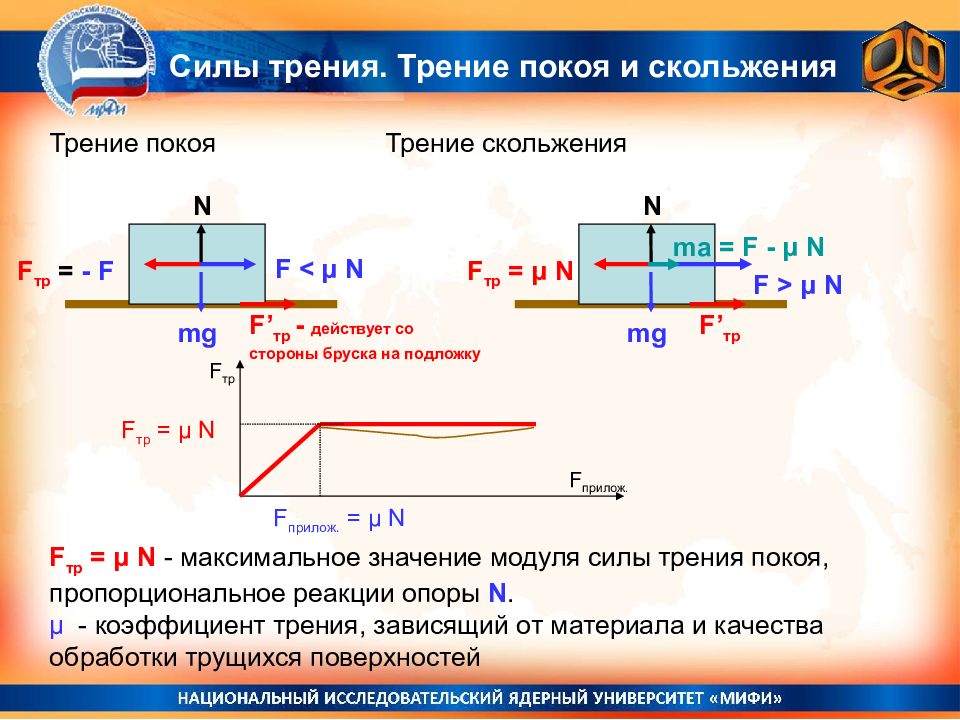 10. Напишите выражение для определения силы трения скольжения.    11. Перечислите факторы, влияющие на размер коэффициента трения скольжения. https://studfile.net/preview/3845244/page:17/ https://studref.com/366768/stroitelstvo/faktory_vliyayuschie_trenie_skolzheniya 12. Выведите формулу для определения предельного угла наклона плоскости к горизонту при котором начинает соскальзывать тело с наклонной плоскости.  13. трение качения https://obrazovaka.ru/fizika/sila-treniya-kacheniya-formula.html + см документ 14. В чем заключается различия свободных и вынужденных колебаний? Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Ярким примером свободных колебания является колебания груза, прикреплённого к пружине, или груза, подвешенного на нити Свободные колебания происходят "сами по себе", без воздействия внешних периодически изменяющихся сил. Движение качелей, которые кто-то периодически подталкивает, это вынужденные колебания. https://studopedia.ru/14_52166_kolebaniya-svobodnie-vinuzhdennie-avtokolebaniya-parametricheskie-kolebaniya.html 15. В чем заключается явление резонанса? Чем определяется величина максимально возможной амплитуды колебаний при резонансе? https://wika.tutoronline.ru/fizika/class/9/opredelenie-yavleniya-rezonansa--v-chem-zaklyuchaetsya Быстрый ответ Амплитуды колебаний при резонансе определяются из условия равенства работ возмущающих сил и сил сопротивлений за каждый цикл колебаний. Расчет выполняется в основном для резонансных режимов, так как они наиболее опасны. Приравнивая работу возбуждающих крутящих моментов работе моментов сопротивлений за период одного колебания, находят резонансные амплитуды всех масс системы. https://cyberleninka.ru/article/n/amplitudy-kolebaniy-pri-rezonanse/viewer 16. Каким образом можно увеличить/уменьшить добротность колебательной системы? https://zetlab.com/podderzhka/vibratsionnyie-ispyitaniya/teoriya-vibroispyitaniy/udarnyiy-spektr-i-dobrotnost-kolebatelnoy-sistemyi/ https://studopedia.ru/9_89398_dobrotnost.html 17. Приведите примеры механического резонанса в известных вам системах. Различные примеры механического резонанса включают: Музыкальные инструменты ( акустический резонанс ) Большинство часов отсчитывают время за счет механического резонанса в колесе баланса , маятнике или кристалле кварца Приливные резонанс в заливе Фанди Орбитальный резонанс , как в некоторых спутниках из Солнечной системы «s газовых гигантов Резонанс базилярной мембраны в ухе Бокал разбивается, когда кто-то громко поет с нужной тональностью 18. Какие колебания называют установившимися и почему? Установившиеся колебания (вибрация) – периодические или почти периодические колебания (вибрация) системы, которые устанавливаются в системе по прошествии некоторого времени после начала колебаний. найдено на slovaronline.com Если значение вынуждающей силы увеличивать, то можно получить резкое возрастание амплитуды колебаний — явление резонанса колебаний. Для установления постоянных амплитуды и частоты вынужденных колебаний необходимо время. Установившимися вынужденными колебаниями называют гармонические колебания с частотой вынуждающей силы. Перемешивая ложкой напитки в чашке, мы заставляем частицы жидкости совершать колебания с частотой вращения ложки. Если суммарная работа сил трения и внешних сил за каждый период равна нулю, то механическая энергия колебательной системы за время, разное периоду колебании не изменяется. В этом случае амплитуда колебаний остается постоянной. Такие колебания называют установившимися вынужденными колебаниями. В случае, если работа внешних сил компенсирует потери энергии колебательной системы, обусловленные [рением, колебания называют установившимися.  19. Что такое звук? Укажите объективные характеристики звукового тона. https://blog.fenix.help/zalipatelnaya-nauka/osnovnyye-ponyatiya-fizicheskiy-smysl-zvuka Объективные характеристики — это частота и интенсивность звука. Второй подход базируется на восприятии звука слуховым аппаратом человека — ухом (субъективные характеристики). Количество энергии, которая переносится за одну секунду через площадку в один квадратный метр, размещенную перпендикулярно направлению распространения волны, называют интенсивностью звука или силой звука. | |||||||||
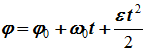,,) Ине́рция — явление сохранения скорости. Момент инерции твердого тела - относительно оси равен сумме моментов инерции всех материальных точек, составляющих это тело, теорема Гюйгенса – Штейнера 
), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: .
, действующий на вращательное тело, равен изменению его момента импульса 
” ( 
) Закон сохранения момента импульса. - момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени ( 
.)