Реферат по Диагностике и надёжности. Реферат. Метод кратчайших путей и минимальных сечений
 Скачать 47.03 Kb. Скачать 47.03 Kb.
|
|
Министерство образования и науки Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ДИЗАЙНА» ВЫСШАЯ ШКОЛА ТЕХНОЛОГИИ И ЭНЕРГЕТИКИ Институт безотрывных форм обучения Кафедра информационно-измерительных технологий и систем управления РЕФЕРАТпо дисциплине «Диагностика и надёжность автоматизированных систем» на тему: Метод кратчайших путей и минимальных сечений
Санкт-Петербург 2019 Содержание
1 Введение Часто бывает полезно и наглядно изображать некоторую ситуацию в виде рисунка, который состоит из точек (вершин), изображающие основные элементы ситуации, и линий (ребер), которые соединяют определенные пары этих вершин и изображают связи между ними. Такие рисунки известны под общим названием – графы. Графы встречаются во многих областях под разными названиями: «структуры» в гражданском строительстве, «сеть» в электротехнике, «социограммы» в социологии и экономике, «молекулярные структуры» в химии, «дорожные карты» и другие. Бурное развитие вычислительной техники позволяет решать все более сложные теоретические и прикладные задачи, в свою очередь требует совершенствования методов их решения. Широкое распространение технологии параллельных и распределенных вычислений позволяет по-новому взглянуть на решение многих задач, а также на методы и алгоритмы, раньше казались бесперспективными из-за высокой вычислительной сложности. В задачи высокой вычислительной сложности относятся частности задачи оптимизации. Одной из таких задач является задача поиска кратчайшего пути на графе. Задача имеет много практических применений, в их число можно отнести поиск кратчайшего пути между городами, поиск пути передачи информации, который обеспечивает минимальную стоимость и минимальное количество времени передачи или максимальную надежность при распространении информации в разветвленной сети. 2 Общие сведения Проблема поиска кратчайших путей в графе является общеизвестной и важной для различных приложений. Существует ряд алгоритмов для решения этой задачи. В последнее время эта проблема интенсивно изучается для графов сложной многоуровневой структуры. Граф – это совокупность объектов со связями между ними. Объекты рассматриваются как вершины, или узлы графа, а связи – как дуги, или ребра. Для различных областей использования виды графов могут отличаться ориентируемостью, ограничениями на количество связей и дополнительными данными о вершинах или ребра. Большое количество структур, которые имеют практическую ценность в математике и информатике, могут быть представлены графами. Граф G – это упорядоченная пара G = (V; E), для которой выполняются следующие условия: V – множество вершин или узлов E – множество пар (в случае неориентированного графа – неупорядоченных) вершин, которые называют ребрами V и E обычно считаются конечными множествами. Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф. Неориентированный граф – это граф (рисунок 1), для каждого ребра которого несуществен порядок двух его конечных вершин. 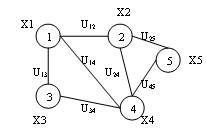 Рисунок 1 – Пример помеченного неориентированного графа Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин (рисунок 2). 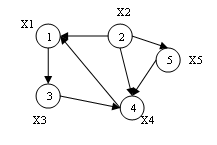 Рисунок 2 – Пример ориентированного графа Смешанный граф (рисунок 3) – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой из перечисленных видов графа может содержать одно или несколько ребер, у которых оба конца сходятся в одной вершине, такие ребра называются петлями (рисунок 4). 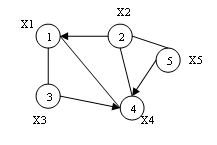 Рисунок 3 – Пример смешанного графа 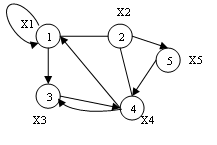 Рисунок 4 – Пример смешанного графа с петлями Если пара вершин соединяется несколькими ребрами или дугами одного направления, то ребра (дуги) называют кратными (параллельными). Дуга или ребро, соединяющий вершину саму с собой, называется петлей. Граф без кратных дуг и петель называется простым. Степень вершины – количество ребер графа G, инцидентных вершине x. Вес ребра – значение, поставлены в соответствие данному ребру взвешенного графа. Обычно вес – действительное число, в таком случае его можно интерпретировать как «длину» ребра. Граф, в котором каждому ребру (каждой дуге) поставлено в соответствие определенное неотрицательное число, которое называют весом или длиной ребра (дуги), называют взвешенным графом. Путем в графе называют конечную последовательность вершин, в которой каждая вершина соединена ребром с последующей в последовательности вершин. Дуги, имеющие общие конечные вершины, называются смежными. Путь (или цикл) называют простым, если ребра в нем не повторяются; элементарным, если он простой и вершины в нем не повторяются. Ориентированным путем в орграф называют конечную последовательность вершин V i, для которой все пары (Vi, V i + 1) есть (ориентированными) ребрами. Длиной пути (маршрут) во взвешенном графе называют сумму длин звеньев этого пути (маршрут). Количество k ребер в пути называется длиной пути. Говорят, что этот путь соединяет вершины v1 и vk +1 или ведет с вершины v1 в вершину vk +1.Путем длины 0 считается последовательность, состоящая из единственной вершины. Путь, в котором все ребра попарно различны, называется цепью. Путь, в котором все промежуточные вершины попарно различны, называется простой цепью. Путь называют циклом, если в нем первая и последняя вершины совпадают. 3 Обзор алгоритмов для поиска кратчайших путей Проблема поиска оптимальных решений является базовой в различных областях науки и техники и требует разработки средств эффективного решения. Часто оптимизационные задачи можно свести к задачам формализованного вида и взаимосвязь составных частей математической модели представить в виде графа. Такой подход позволяет использовать алгоритмы и средства теории графов в процессе поиска оптимальных решений и минимизации аналитических моделей критериев оптимальности. Решение задачи тогда сводится к поиску кратчайших путей между вершинами графа. Широкий круг оптимизационных задача сводится к описанию математической модели системы с помощью средств теории графов с определением физического смысла массива вершин и дуг, которые соединяют. Оптимальное решение тогда может быть найдено по определенному алгоритму теории графов с помощью автоматизированной системы поиска оптимальных решений: – для поиска кратчайшего пути между двумя вершинами графа используется алгоритм Дейкстры, который требует меньше временных затрат по сравнению с подобными алгоритмами; – поиск кратчайших путей между всеми вершинами графа осуществляется с помощью алгоритма Флойда; – найти минимальный путь в графе с ребрами единичной длины позволяет волновой алгоритм. Список использованной литературы Ногина Н.В. Синтез регулярного выражения языка, порожденного помеченным графом, методом его локальной редукции / Н.В. Ногина, И.С. Грунский // Искусственный интеллект. – 2012. – №3. – с. 348-353. Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с. Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с. Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с. | ||||||||||||||||||||||
