лр. Метод локализации корня графически
 Скачать 108.76 Kb. Скачать 108.76 Kb.
|
|
Пусть задана непрерывная функция 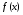 , и требуется найти все или некоторые корни уравнения , и требуется найти все или некоторые корни уравнения 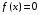 . Для решения задачи необходимо: . Для решения задачи необходимо: исследовать количество, характер и расположение корней (простые или кратные, действительные или комплексные); найти приближенные значения для корней; провести вычисления приближенных значений с заданной точностью. Теорема 1: Если непрерывная функция 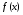 принимает значения разных знаков на концах отрезка принимает значения разных знаков на концах отрезка 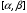 , то есть , то есть 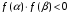 , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения 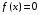 , то есть найдется хотя бы одно число , то есть найдется хотя бы одно число 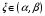 такое, что такое, что 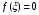 . .Метод локализации корня графически Действительные корни уравнений 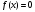 приближенно можно определить как абсциссы точек пересечения графика функции приближенно можно определить как абсциссы точек пересечения графика функции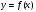 с осью с осью 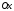 . Таким способом можно легко определить корни данного уравнения, если они находятся на достаточном расстоянии друг от друга. На практике часто бывает выгодно заменить . Таким способом можно легко определить корни данного уравнения, если они находятся на достаточном расстоянии друг от друга. На практике часто бывает выгодно заменить 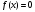 равносильным ему уравнением: равносильным ему уравнением: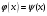 где функции 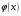 и и 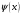 – более простые, чем функция – более простые, чем функция 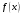 . .Построив графики функций 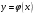 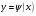 , искомые корни получим как абсциссы точек пересечения этих графиков. , искомые корни получим как абсциссы точек пересечения этих графиков.Метод дихотомии Для нахождения корня уравнения 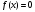 , принадлежащего отрезку , принадлежащего отрезку 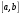 , делим этот отрезок пополам. Если , делим этот отрезок пополам. Если 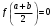 , то , то 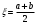 является корнем уравнения. Если является корнем уравнения. Если 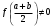 , то выбираем ту из половин , то выбираем ту из половин 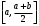 или или 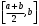 , на концах которой функция , на концах которой функция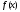 имеет противоположные знаки. Новый отрезок имеет противоположные знаки. Новый отрезок 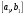 снова делим пополам и проводим то же рассмотрение и т.д. В результате получаем на каком-то этапе искомый корень уравнения. снова делим пополам и проводим то же рассмотрение и т.д. В результате получаем на каком-то этапе искомый корень уравнения.Метод секущих Данный метод применяется при решении уравнений вида 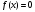 , если корень уравнения отделен. , если корень уравнения отделен. Первое приближение корня находится по формуле: 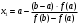 Для следующего приближения из отрезков 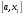 и и 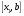 выбирается тот, на концах которого функция выбирается тот, на концах которого функция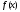 имеет значения разных знаков. имеет значения разных знаков.Тогда второе приближение вычисляется по формуле: 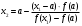 , если , если 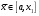 Или 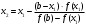 , если , если 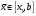 Метод простых итераций Другим важным методом нахождения корней уравнения является метод итераций. Сущность этого метода заключается в следующем: Пусть дано уравнение 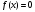 , где , где 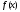 – непрерывная функция, и требуется определить его вещественные корни. Заменим данное уравнение равносильным уравнением – непрерывная функция, и требуется определить его вещественные корни. Заменим данное уравнение равносильным уравнением 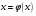 . .Допустим, что для искомого корня уравнения 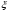 указано начальное приближение, дальнейшие приближения строятся по формуле указано начальное приближение, дальнейшие приближения строятся по формуле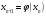 , ,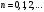 Для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса, для этого воспользуемся следующей теоремой. Теорема 2: Пусть функция 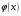 определена и дифференцируема на отрезке определена и дифференцируема на отрезке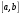 , причем все ее значения , причем все ее значения 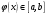 ,тогда, если существует правильная дробь ,тогда, если существует правильная дробь 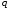 такая, что такая, что 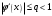 при при 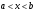 , то , то1) процесс итерации 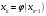 , ,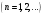 Сходится независимо от начального значения 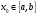 ; ;2) предельное значение 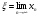 является единственным корнем уравнения является единственным корнем уравнения 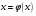 на отрезке на отрезке 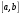 . .Метод Ньютона Данный метод применяется, если уравнение 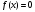 имеет корень имеет корень 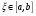 и выполняются условия: и выполняются условия: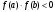 Производные 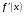 и и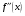 сохраняют знак на отрезке сохраняют знак на отрезке 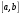 . .На отрезке 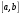 выбирается такое число выбирается такое число 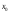 , при котором выполняется условие , при котором выполняется условие 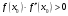 . .Первое приближение корня определяется по формуле: 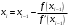 , где , где 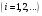 |
