Метод поиска Хука – Дживса - MathCad. Метод поиска Хука Дживса
 Скачать 94.5 Kb.
|
Метод поиска Хука – ДживсаПроцедура Хука и Дживса представляет собой комбинацию двух типов поиска: исследующий поиск и поиск по образцу. Исследующий поиск ориентирован на выявление характера локального поведения целевой функции и определение направлений вдоль “оврагов”.  Рис Первые 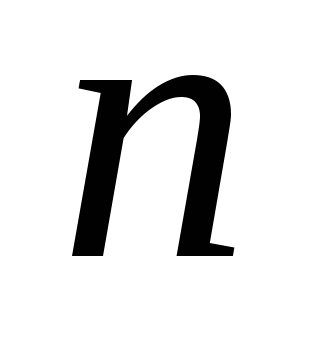 шагов исследующего поиска осуществляются аналогично первым 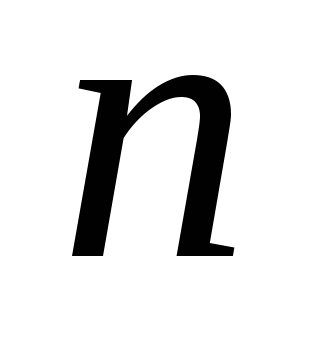шагам покоординатного спуска. Для проведения исследующего поиска необходимо задать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значения функции в исходной точке, то шаг поиска рассматривается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех 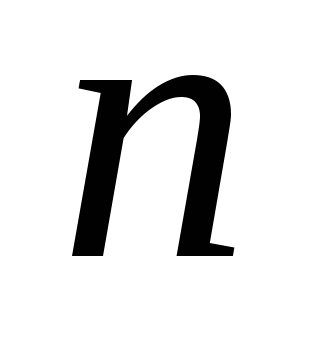координатных направлений исследующий поиск завершается. Полученную в результате точку называют базисной точкой.Поиск по образцу заключается в реализации единственного шага из полученной базисной точки вдоль прямой, соединяющей эту точку с предыдущей базисной точкой. Новая точка образца определяется в соответствии с формулой 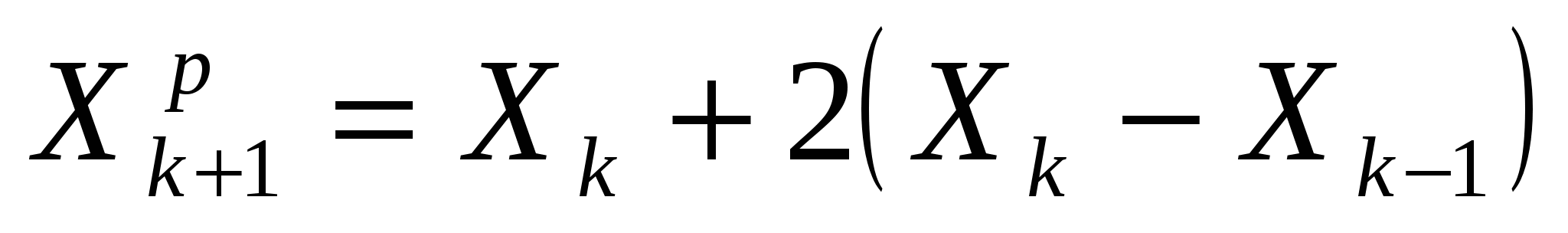 .Движение по образцу считается успешным, если исследующий поиск, проведенный из точки 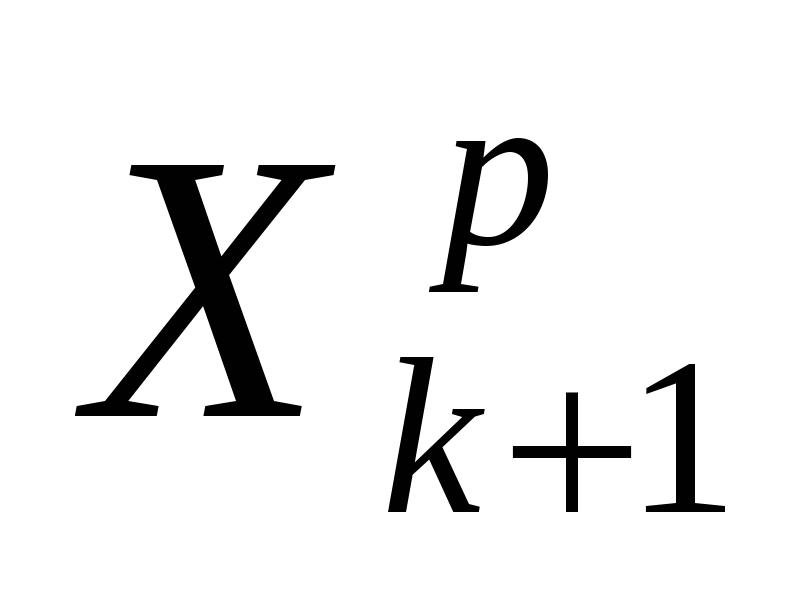 , приводит к уменьшению целевой функции. В этом случае полученная точка рассматривается как новая базисная точка 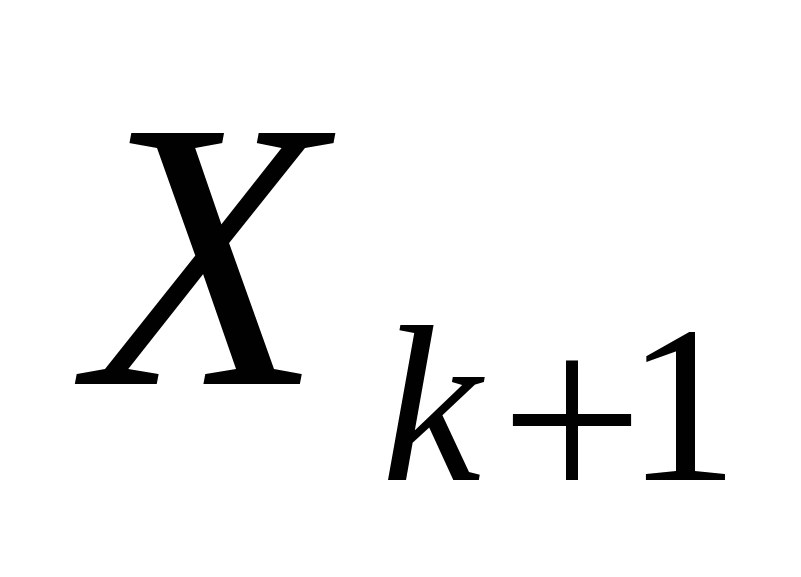 . Если исследующий поиск, проведенный после поиска по образцу, неудачен, то необходимо вернуться в точку  и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете, возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага при исследующем поиске (например в 10 раз) и возобновить исследующий поиск. Поиск завершается, когда величина исследующего шага становится достаточно малой. |