|
|
Изучите выдержки из представленных в прил. 1–9 нормативных документов и назовите статьи законодательных актов, устанавливающие о. Кратко о методах. Метод половинного деления|
|
 Скачать 54.26 Kb. | Название | Метод половинного деления | | Анкор | Изучите выдержки из представленных в прил. 1–9 нормативных документов и назовите статьи законодательных актов, устанавливающие о | | Дата | 22.11.2021 | | Размер | 54.26 Kb. | | Формат файла |  | | Имя файла | Кратко о методах.docx | | Тип | Документы
#278732 |
|
Методы приближенного решения уравнений вида f(x)=0
Метод половинного деления
Если 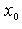 и и 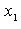 таковы, что таковы, что 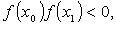 то полагаем то полагаем 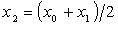 и вычисляем и вычисляем 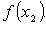 Если Если 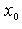 то корень найден. В противном случае из отрезков то корень найден. В противном случае из отрезков 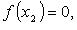 и и 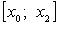 выбираем тот, на концах которого f принимает значения разных знаков, и проделываем аналогичную операция. Процесс продолжаем до получения требуемой точности. выбираем тот, на концах которого f принимает значения разных знаков, и проделываем аналогичную операция. Процесс продолжаем до получения требуемой точности.
Метод простых итераций
Уравнение f(x) = 0 преобразуем к виду 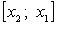 Выбираем некоторое приближение Выбираем некоторое приближение 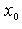 искомого корня, последующие приближения вычисляем по формуле искомого корня, последующие приближения вычисляем по формуле
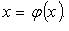
При выполнении определенных условий последовательность 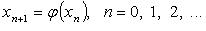 сходится к сходится к 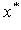 - корню уравнения f(x) = 0. - корню уравнения f(x) = 0.
Метод Ньютона (метод касательных)
Если 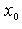 - начальное приближение корня уравнения f(x) = 0, то последовательные приближения находят по формуле - начальное приближение корня уравнения f(x) = 0, то последовательные приближения находят по формуле
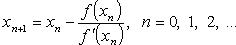
Если f' и f'' непрерывны и сохраняют определенные знаки на отрезке 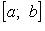 , а f(a)f(b) < 0 , то, исходя из начального приближения , а f(a)f(b) < 0 , то, исходя из начального приближения 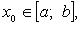 удовлетворяющего условию удовлетворяющего условию 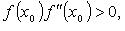 можно вычислить с любой точностью единственный корень уравнения f(x) = 0. можно вычислить с любой точностью единственный корень уравнения f(x) = 0.
Метод секущих (метод хорд)
Если 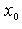 , , 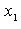 - приближенные значения корня уравнения f(x) = 0 , а - приближенные значения корня уравнения f(x) = 0 , а 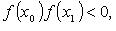 то последующие приближения находят по формуле то последующие приближения находят по формуле
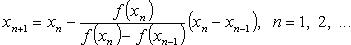
Методом хорд называют также метод, при котором один из концов отрезка 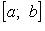 закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по формулам: закреплен, т. е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:
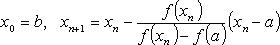
либо
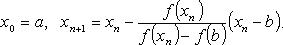
При этом предполагается, что корень уравнения находится на отрезке 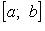 , а f''(x) сохраняет знак на , а f''(x) сохраняет знак на 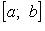 . . |
|
|
 Скачать 54.26 Kb.
Скачать 54.26 Kb.