Вычислить определенный интеграл методами прямоугольников. Егоров Богдан. Метод прямоугольников
 Скачать 118.86 Kb.
|
|
3. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при   Метод прямоугольников Это самая простая квадратурная формула вычисления интеграла, в которой используется одно значение функции:   h = b - a = 2.66-0.5 = 2.16  f(c) = 21.29  Остаточный член квадратурной формулы:   Найдем максимальное значение второй производной функции на интервале [0.5;2.66].   Формула трапеций аналогична формулам прямоугольников, но функция y=f(x) заменяется на каждом отрезке [xi, xi+1] отрезком прямой Δx. Формула трапеций:  
= 0.216*240.97 =  Остаточный член квадратурной формулы:  Найдем максимальное значение второй производной функции на интервале [0.5;2.66].  Таким образом, I = 52.05 ± 0.1238 Формула Симпсона основана на замене подынтегральной функции f(x) на отрезке [a, b] дугой параболы, т.е. функция f(x) аппроксимируется параболой вида: P(x)=αx2 + βx + γ. Разобъем отрезок [a, b] на четное число равных отрезков n = 2m, при этом точки x0, x2, x4, ... , xn-2, xn - точки деления (x0 = a, xn = b). Обозначим через x1, x3, x5, ... середины отрезков [x0, x2], [x2, x4], [x4, x6] и т.д. Применив для каждого отрезка разбиения элементарную формулу Симпсона, получим формулу парабол. Формула Симпсона: 
Остаточный член квадратурной формулы:  Найдем максимальное значение четвертой производной функции на интервале [0.5;2.66].  Таким образом, I = 51.93 ± 3.1E-5 Функция задана таблично
Построить аппроксимирующую прямую  , используя метод наименьших квадратов (решить сначала вручную, затем в Excel).Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: an + b∑x = ∑y a∑x + b∑x2 = ∑y*x
Для наших данных система уравнений имеет вид: 7a + 16.5b = 34.15 16.5a + 48.75b = 100.14 Из первого уравнения выражаем a и подставим во второе уравнение Получаем a = 0.181, b = 1.993 Уравнение тренда: y = 1.993 x + 0.181 Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Коэффициент тренда b = 1.993 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени x на единицу его измерения. В данном примере с увеличением x на 1 единицу, y изменится в среднем на 1.993. Изучена временная зависимость Y от времени x. На этапе спецификации был выбран линейный тренд. Оценены его параметры методом наименьших квадратов. Возможна экономическая интерпретация параметров модели - с каждым периодом времени x значение Y в среднем увеличивается на 1.993 ед.изм. Дана задача Коши для обыкновенного дифференциального уравнения I порядка: 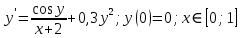 Найти численное решение задачи методами Эйлера и Рунге-Кутта при .
|
