Аддадад. Метод золотого сечения
 Скачать 89.3 Kb.
|
|
Метод золотого сечения Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения и эффективен при n-2, что и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции. Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3). 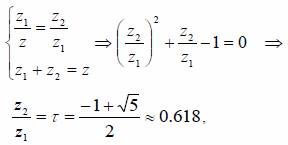 где τ - «золотое сечение» 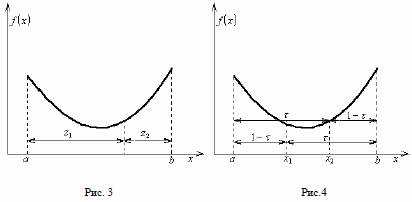 На каждом шаге этой итеративной процедуры, кроме первого, вычисляется только одно значение функции. Однако Химмельблау рекомендовал вычислять на каждом шаге две точки, для того чтобы не накапливалась погрешность, так как τ имеет приближенное значение (рис 4). Если длина конечного интервала неопределенности равна δ, то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию   ПРИМЕР. Методом золотого сечения найти точку минимума x* функции f(x) на отрезке [a;b] с точностью ε и значение целевой функции в этой точке: f(x)=x4+2x2+4x+1=0, [-1;0], ε=0.1 Решение. Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 - a1), μ1 = a1 + 0.618(b1 - a1). Вычислим f(λ1) = -0.5623, f(μ2) = -0.2149 Итерация №1. Поскольку f(λ1) < f(μ1), то b2 = -0.382, a2 = a1, μ2 = -0.618 μ2 = a2 + 0.618(b2 - a2) = -1 + 0.618(-0.382 +1), f(μ2) = f(-0.618) = -0.2149 Итерация №2. Поскольку f(λ2) > f(μ2), то a3 = -0.7639, b3 = b2, λ3 = -0.618 μ3 = a3 + 0.618(b3 - a3) = -0.7639 + 0.618(-0.382 +0.7639), f(μ3) = f(-0.5279) = -0.5623 Итерация №3. Поскольку f(λ3) < f(μ3), то b4 = -0.5279, a4 = a3, μ4 = -0.618 μ4 = a4 + 0.618(b4 - a4) = -0.7639 + 0.618(-0.5279 +0.7639), f(μ4) = f(-0.618) = -0.4766 Итерация №4. Поскольку f(λ4) < f(μ4), то b5 = -0.618, a5 = a4, μ5 = -0.6738 μ5 = a5 + 0.618(b5 - a5) = -0.7639 + 0.618(-0.618 +0.7639), f(μ5) = f(-0.6738) = -0.5623 Остальные расчеты сведем в таблицу.
Находим x как середину интервала [a,b]: x=(-0.618-0.70818104)/2 = -0.66309052. Ответ: x = -0.66309052; F(x) = -0.57965758 Метод Фибоначчи Описание метода Пусть задана функция 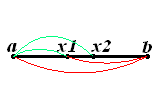 Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки  и  таки, что: Иллюстрация выбора промежуточных точек метода золотого сечения. Иллюстрация выбора промежуточных точек метода золотого сечения. Реклама 08  , где  — пропорция золотого сечения.Таким образом: 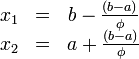 То есть точка делит отрезок  в отношении золотого сечения. Аналогично делит отрезок  в той же пропорции. Это свойство и используется для построения итеративного процесса.Алгоритм На первой итерации заданный отрезок делится двумя симметричными относительно его центра, точками и рассчитываются значения в этих точках. После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают. На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку. Процедура продолжается до тех пор, пока не будет достигнута заданная точность. Формализация Шаг 1. Задаются начальные границы отрезка  и точность  , рассчитывают начальные точки деления:  и значения в них целевой функции:  .Шаг 2. Если  , то  .Иначе  .Шаг 3. Если  , то  и останов.Иначе возврат к шагу 2. |