ЛПР 10. Методы одномерной оптимизации
 Скачать 2 Mb.
|
|
ТИПОВЫЕ ЗАДАЧИ Задача 1. Определить отрезок, содержащий точку максимума функции  ;  ;  .Решение.  ; ; . Поскольку  , ,  . Далее  ,  , . , . , . .Задача 2. Найти точку максимума функции  на отрезке  методом дихотомическиого поиска.  ;  . Решение. Итерация 1.  , ; ;  ; ; ,  ;  .Итерация 2.  , ; ;  ; ; ,  ;  .Итерация 3.  , ; ;  ; ; ,  .Итерация 4.  ;  .Задача 3. Найти точку максимума функции  на отрезке методом золотого сечения,  . Решение.  ;  ;  . . . ;  . Итерация 1. Так как , то  ;  . ;  ; ; ; . Итерация 2. Так как , то  ;  . ;  ; ; ; . Итерация 3. Так как , то  ;  . ;  ; ; ; .Итерация 4. Так как , то  ;  . ;  ; ; ; , следовательно,  .Задача 4. Найти точку максимума функции  на отрезке  методом средней точки,  . Решение.  . Итерация 1.  ;  ;  .Итерация 2.  ;  ;  .Итерация 3.  ;  ;  .Итерация 4.  ;  ;  .Итерация 5.  ;  ;  .Итерация 6.  ;  ;  .Итерация 7.  ;  ;  ,  .Задача 5. Найти точку максимума функции  на отрезке  методом Ньютона-Рафсона,  ;  . Решение. Итерация 1.  ;  ; ;  Итерация 2.  ; ;   Построение графика функции при помощи табличного процессора Microsoft Excel. Пример 1. Дана функция  и отрезок  . Вычислить значения этой функции на заданном отрезке с шагом h. Построить график этой функции на заданном отрезке.Пусть  ;  ;  ;  .Решение Первый этап 1. Открываем новый рабочий лист. 2. Заносим в ячейки А1 и В1 название столбцов -  и  .3. Заносим в ячейки D1, D2 – начальное значение интервала, т.е. точку  , в ячейки Е1, Е2 – конечное значение интервала, т.е. точку  , в ячейки F1, F2 – значение шага табуляции, т.е.  .4. В ячейку А2 вводим формулу  , т.е в ячейку А2 помещаем начальное значение интервала, стоящее в ячейке D2 (абсолютная ссылка ставится нажатием клавиши F4).5. В ячейку А3 вводим формулу изменения аргумента функции на шаг табуляции , т.е. формулу .6. Подводим курсор в правый нижний угол ячейки А3 до появления маленького черного крестика и протяжкой мыши распространяем полученную формулу до ячейки A202, т.е. до получения значения  .7. В ячейку В2 вводим формулу вычисления значения функции в точке , значение которого находится в ячейке А2.8. Подводим курсор в правый нижний угол ячейки В2 до появления маленького черного крестика и протяжкой мыши распространяем полученную формулу до ячейки В202, т.е. до получения значения функции в точке .9. Таким образом, получаем следующую таблицу: 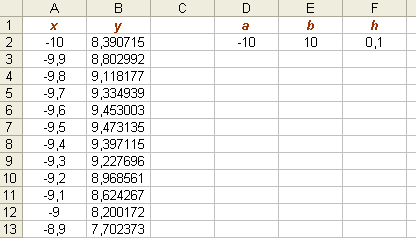 .10. Выделяем ячейки А2:А202 и вызываем Мастер диаграмм кнопкой . Выбираем тип диаграммы – График, вид – График с маркерами, помечающими точки данных, и нажимаем по 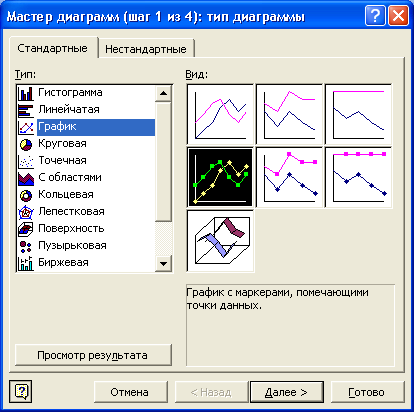 кнопке Далее (рис. 1).11. Устанавливаем Диапазон данных, расположение рядов в столбцах (рис. 2), и нажимаем по кнопке Далее. 12. На третьем шаге построения графика функции вводим Название диаграммы, названия осей x и y (рис. 3). 1 Рис. 1. 3. Указываем расположение диаграммы – На имеющимся листе. 1 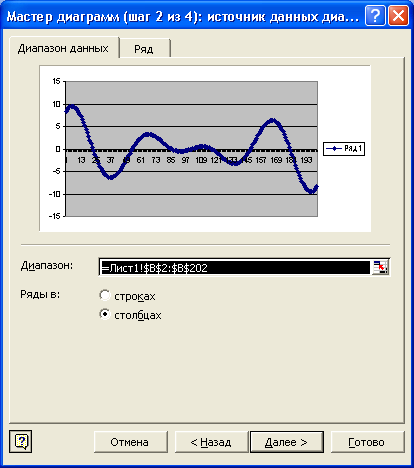 Рис. 2. 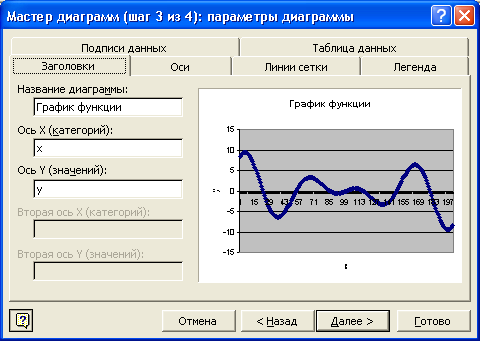 Рис. 3. 4. В результате получает график исходной функции (рис. 4). 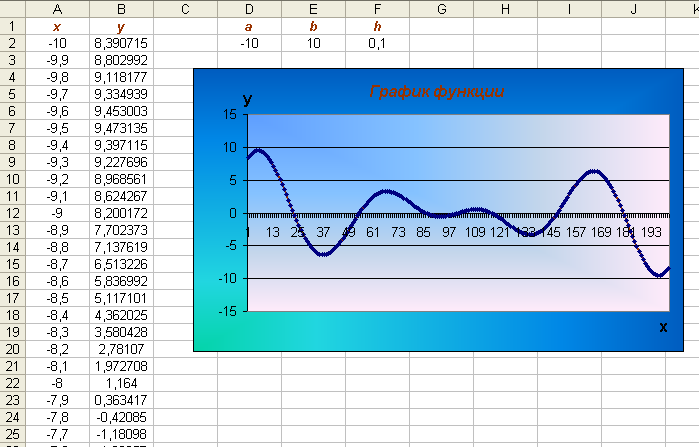 Рис. 4. |