расчетная работа №2 фомичева. Методы оптимизации 1 и 2 порядка

Название	Методы оптимизации 1 и 2 порядка
Дата	09.08.2022
Размер	3.87 Mb.
Формат файла
Имя файла	расчетная работа №2 фомичева.docx
Тип	Документы #642957

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Нижегородский государственный архитектурно-строительный университет»

(ННГАСУ)

институт технологий бизнеса

Кафедра прикладной информатики и статистики

Расчетная работа №2

по теме: Методы оптимизации 1 и 2 порядка.

Вариант - 25

Выполнил студент группы: ПИЭ-20.20 Фомичева А.С.
Проверил доцент, к. физ.-мат. н.: Прокопенко Н.Ю.

г. Нижний Новгород

2022 г

СОДЕРЖАНИЕ

ДАНО 4

ЗАДАНИЯ 4

1.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА 6

1.2. ТЕКСТ ПРОГРАММЫ 7

1.3. БЛОК СХЕМА ПРОГРАММЫ 9

1.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ 10

1.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ 11

2.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА 12

2.2. ТЕКСТ ПРОГРАММЫ 14

2.3. БЛОК СХЕМА ПРОГРАММЫ 16

2.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ 18

2.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ 20

3.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА 21

3.2. ТЕКСТ ПРОГРАММЫ 22

3.3. БЛОК СХЕМА ПРОГРАММЫ 24

3.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ 25

3.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ 27

4.1. СРАВНЕНИЕ ПО КОЛИЧЕСТВАМ ОБРАЩЕНИЙ К ФУНКЦИИ 28

4.2. СРАВНЕНИЕ ТОЧНОСТИ ПРИ ЗАДАННОМ КОЛИЧЕСТВЕ ИТЕРАЦИЙ 28

ЦЕЛЬ РАБОТЫ

Найти экстремум функции методом средней точки, методом хорд и методом Ньютона и провести сравнение данных методов по точности и по количеству итераций.

УСЛОВИЯ ЗАДАЧИ И ЗАДАНИЯ

ДАНО

ЗАДАНИЯ

1. Для функции своего варианта реализовать методы средней точки, метод

хорд и метод Ньютона для поиска точки минимума.

2. Для каждого метода записать формулами расчеты 2 итерации поиска

Минимума.

3. Провести сравнение методов по точности  и по количеству итераций.

4. Оформить отчет.

Данная функция унимодальна на отрезке [-8; 6].

1. МЕТОД СРЕДНЕЙ ТОЧКИ

1.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА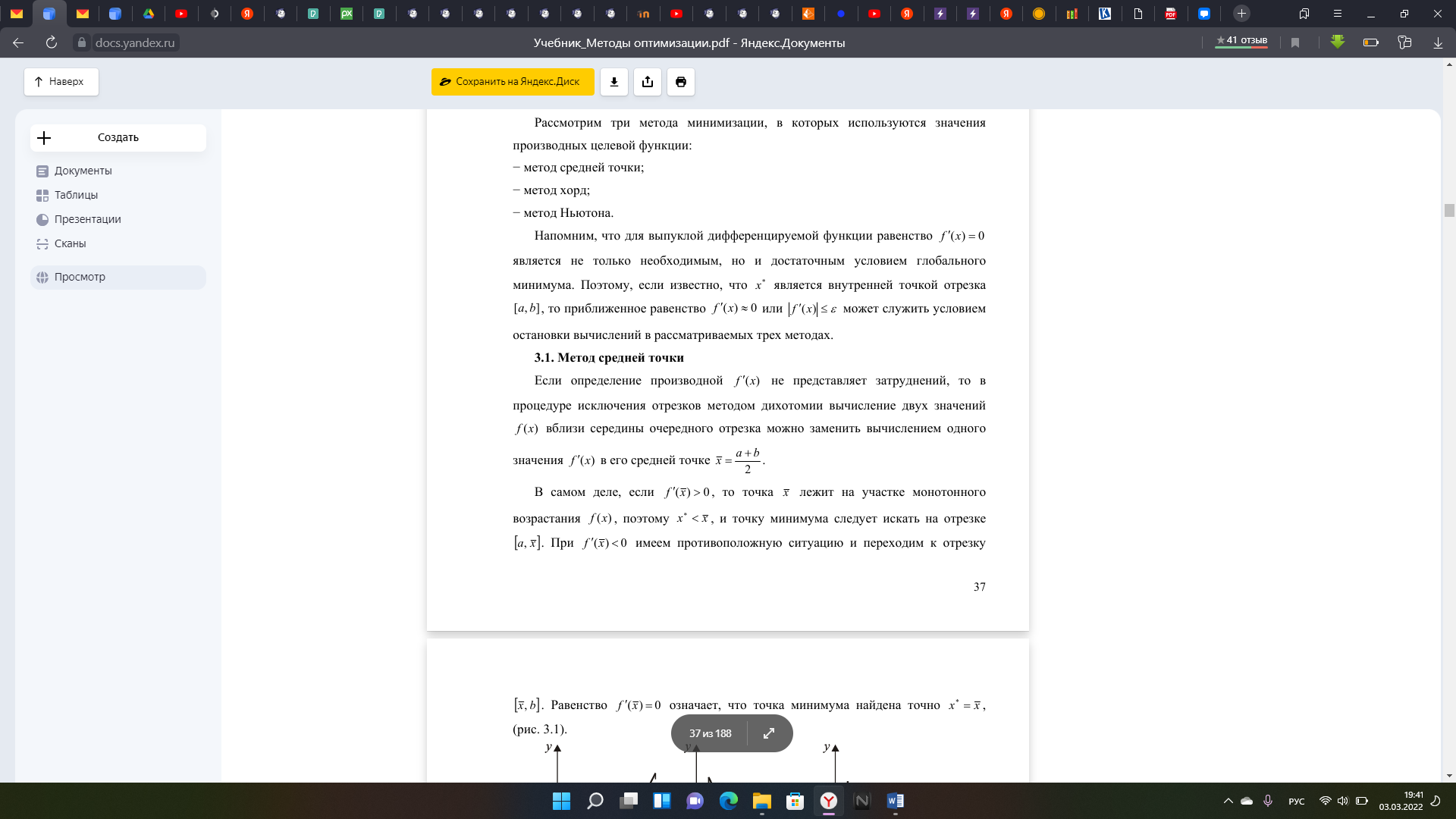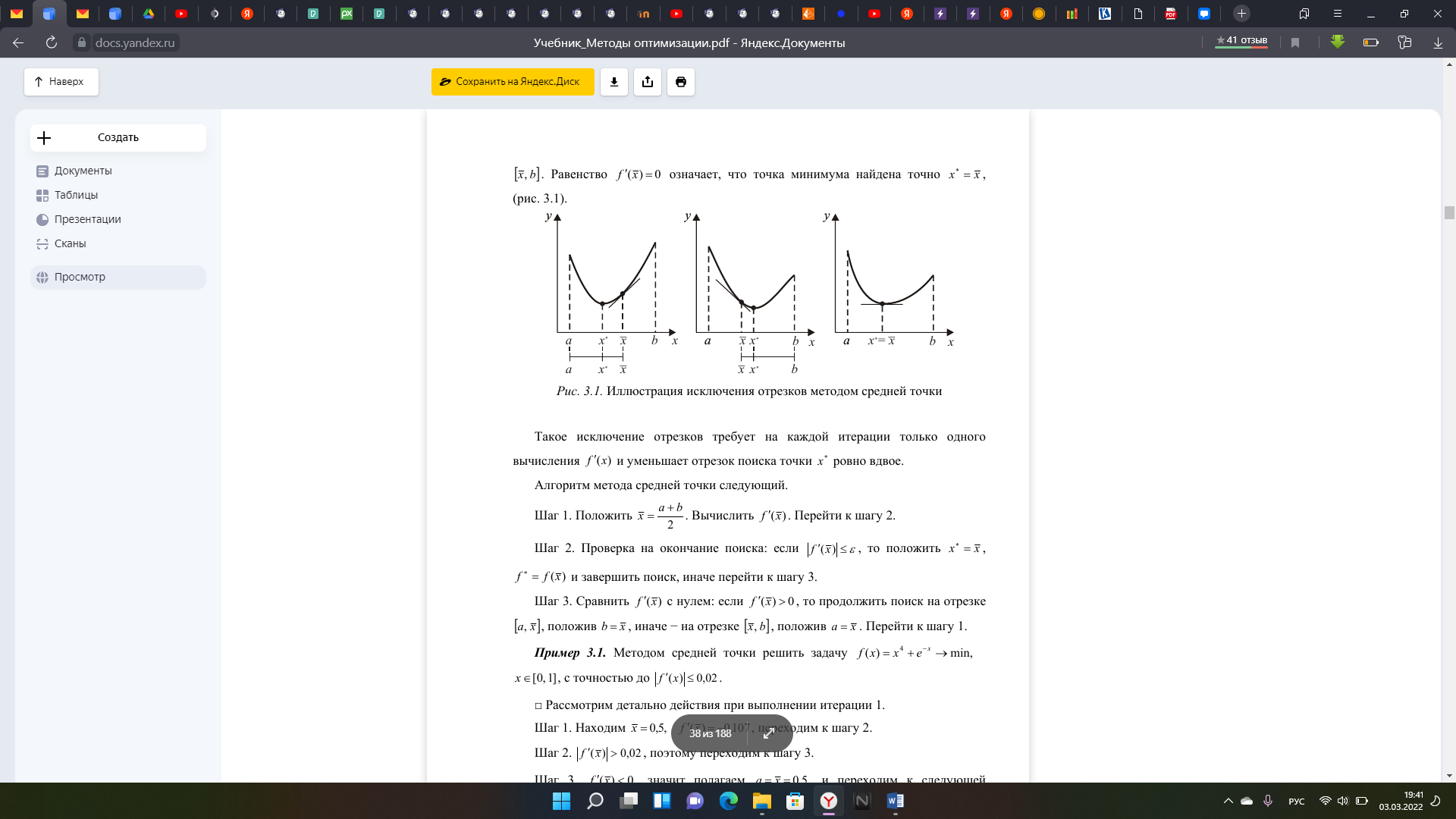

1.2. ТЕКСТ ПРОГРАММЫ

#include

#include

using namespace std;

double func(double x)

{

return (x - 5) * exp(x);

}

double func_1(double x)

{

return (x - 4) * exp(x);

}

int main()

{

setlocale(0, "ru");

double a = -8, b = 6, e = 0.055;

int steps = 0;

int calls = 0;

double x = (a + b) / 2, y;

double f1 = func_1(x);

calls = calls + 1;

action_1:

cout<<"Границы: ["<
if (fabs(f1) <= e)

{

steps = steps + 1;

goto action_2;

}

if (f1 > 0)

{

b = x;

x = (a + b) / 2;

f1 = func_1(x);

calls = calls + 1;

steps = steps + 1;

goto action_1;

}

else

{

a = x;

x = (a + b) / 2;

f1 = func_1(x);

calls = calls + 1;

steps = steps + 1;

goto action_1;

}

action_2:

y = func(x);

cout << "x(наим) = " << x<< ", "<< "y(x) = " << y << ". " << "Number of steps - " << steps <<". "<< endl;

cout << "Количество вызовов функции - " << calls;

}

1.3. БЛОК СХЕМА ПРОГРАММЫ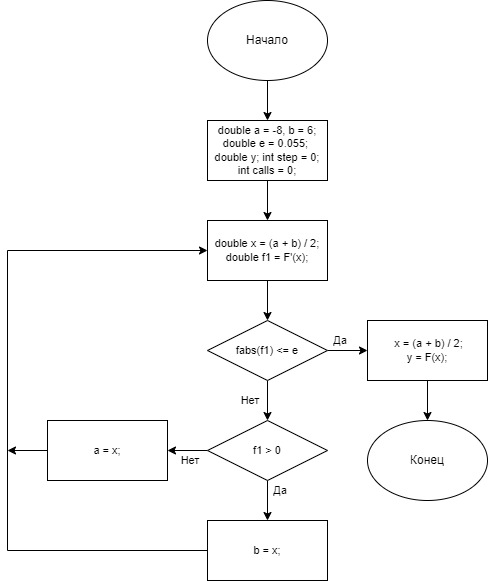

1.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ

1.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ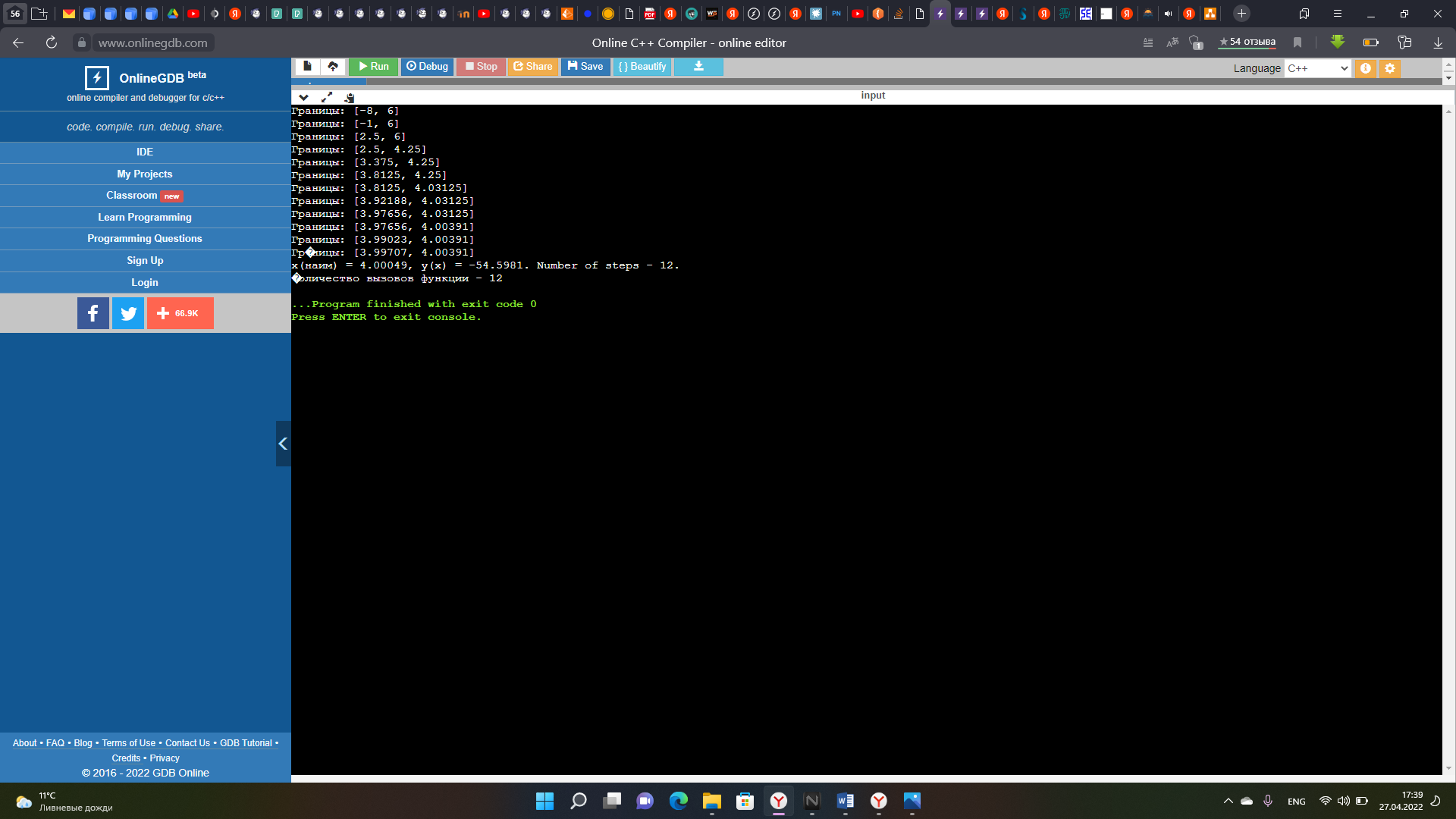

2. МЕТОД ХОРД

2.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА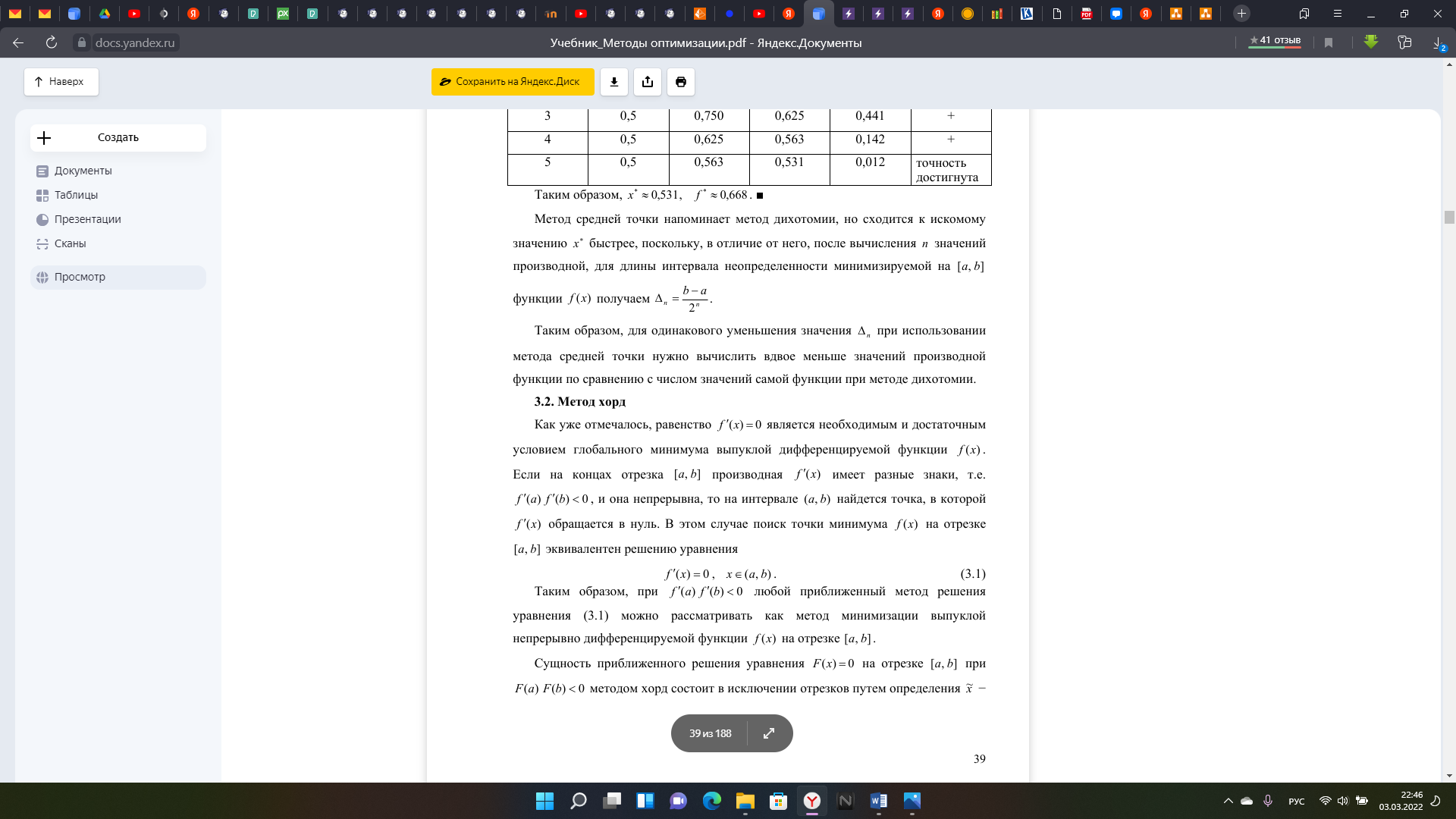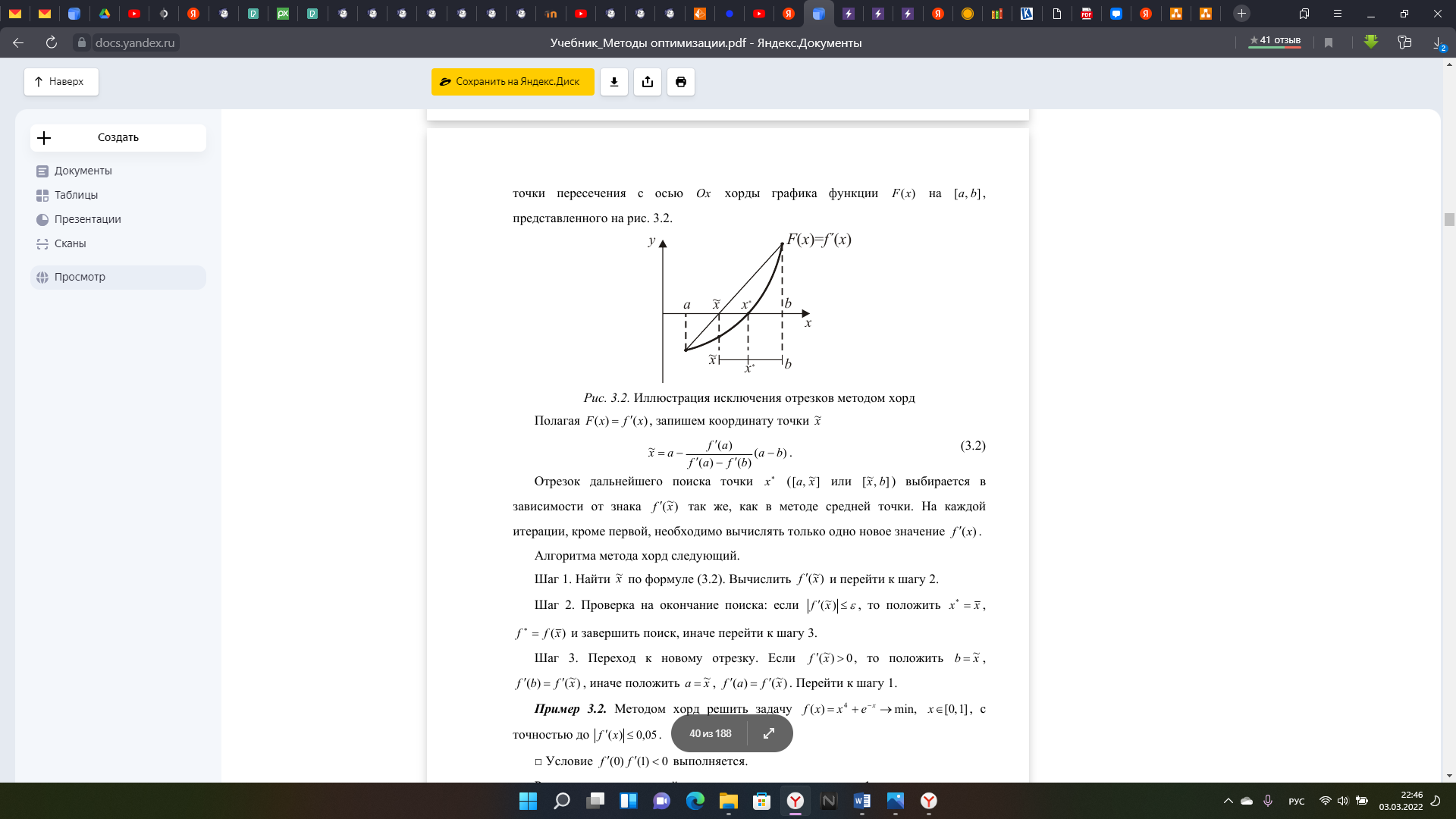

В ходе написания программы мною было выяснено, что программа достигает заданной точности на 1 итерации, поэтому было принято решение уменьшить точность, чтобы программа совершило более одной итерации и верно определила точку минимума заданной функции.

2.2. ТЕКСТ ПРОГРАММЫ

#include

#include

using namespace std;

double func(double x)

{

return (x - 5) * exp(x);

}

double func_1(double x)

{

return (x - 4) * exp(x);

}

int main()

{

setlocale(0, "ru");

double a = -8, b = 6, f1, f2, f3, x0;

double y;

double e = 0.001;

double x;

int count = 1;

int steps = 0;

int calls = 0;

cout<< "Границы: ["<
action_1:

f1 = func_1(a);

f2 = func_1(b);

calls = calls + 2;

if(f1 * f2 < 0)

{

x = a - (f1/(f1 - f2)) * (a - b);

y = func_1(x);

steps = steps + 1;

if(fabs(y)<= e)

{

cout<<"Требуемый уровень точности достигнут. - "<
steps = steps + 1;

goto action_2;

}

if(fabs(y) > e)

{

cout<<"Точность = "<
if(y > 0)

{

b = x;

f2 = y;

steps = steps + 1;

cout<< "Границы: ["<
goto action_1;

}

if(y <= 0)

{

a = x;

f1 = y;

steps = steps + 1;

cout<< "Границы: ["<
goto action_1;

}

}

}

else

{

if(f1 > 0 && f2 > 0)

{

cout<<"Функция возрастает на данном отрезке. "<
x = a;

steps = steps + 1;

goto action_2;

}

if(f1 < 0 && f2 < 0)

{

cout<<"Функция убывает на данном отрезке. "<
x = b;

steps = steps + 1;

goto action_2;

}

if(f1 * f2 == 0)

{

double f3 = func(a);

double f4 = func(b);

if(f3 < f4)

{

x = a;

steps = steps + 1;

goto action_2;

}

if(f3 > f4)

{

x = b;

steps = steps + 1;

goto action_2;

}

}

}

action_2:

cout<
y = func(x);

calls = calls + 1;

cout<<"Ответ: ";

cout << "x(наим) = " << x<< ", "<< "y(x) = " << y << ". " << "Number of steps - " << steps <<". "<< endl;

cout << "Количество вызовов функции - " << calls;

}

2.3. БЛОК СХЕМА ПРОГРАММЫ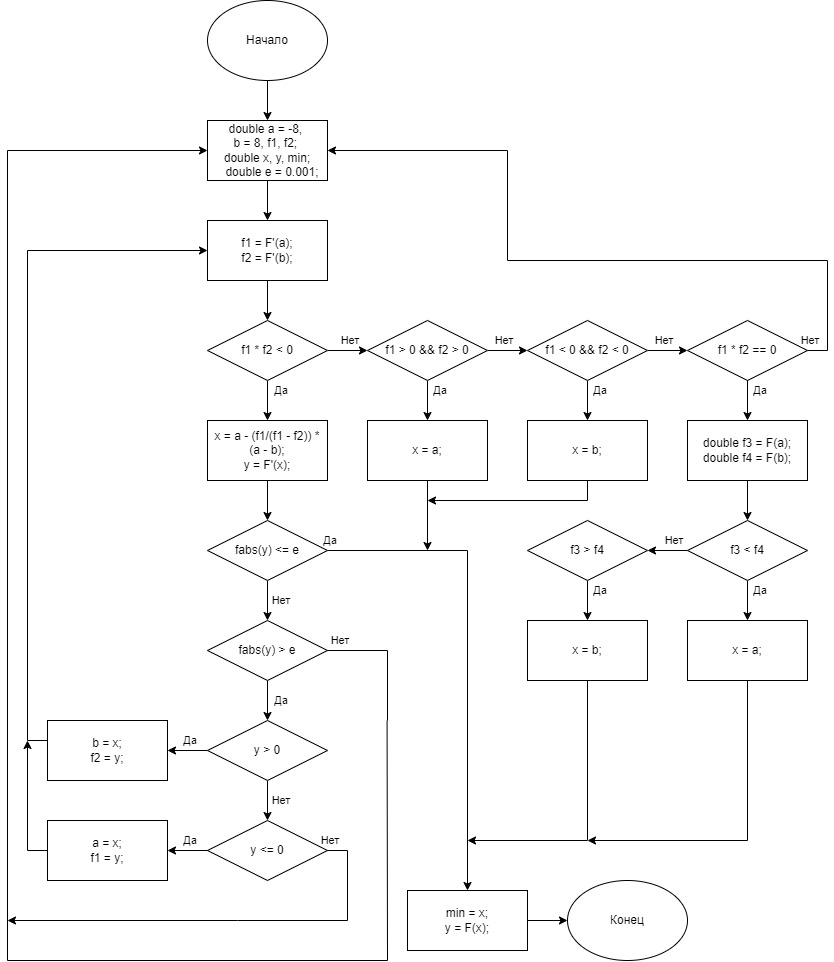

2.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ

2.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ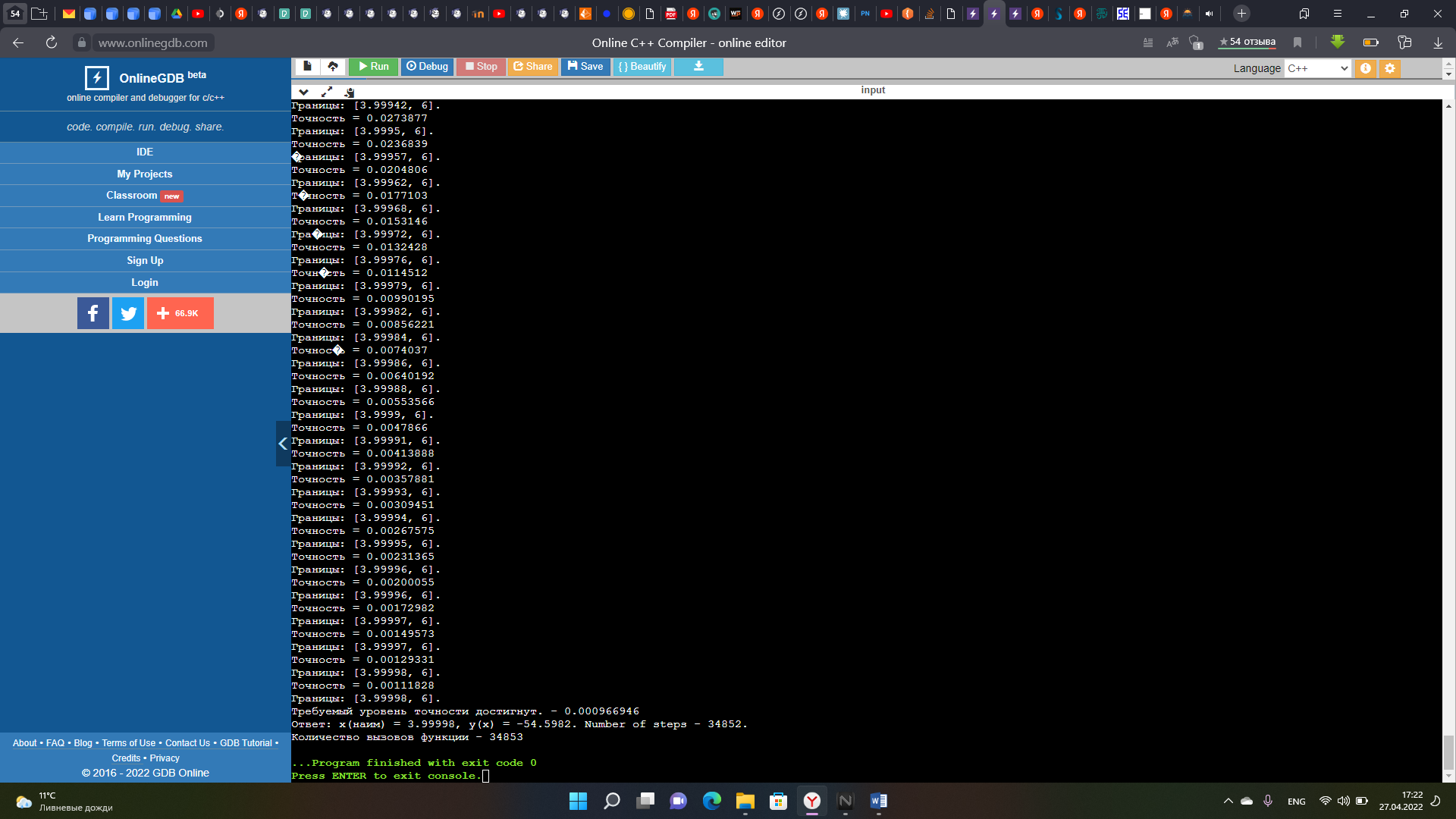

3. МЕТОД НЬЮТОНА

3.1. КРАТКОЕ ОПИСАНИЕ АЛГОРИТМА

3.2. ТЕКСТ ПРОГРАММЫ

#include

#include

using namespace std;

double func(double x)

{

return (x - 5) * exp(x);

}

double func_1(double x)

{

return (x - 4) * exp(x);

}

double func_2(double x)

{

return (x - 3) * exp(x);

}

int main()

{

setlocale(0, "ru");

double a = -8, b = 6, f1, f2, x0;

double y = 0;

double e = 0.055;

double x = b;

int count = 1;

int steps = 0;

int calls = 0;

ac_1:

f1 = func_1(x);

calls = calls + 1;

cout<
cout << "Количество вызовов функции - " << calls;

}

3.3. БЛОК СХЕМА ПРОГРАММЫ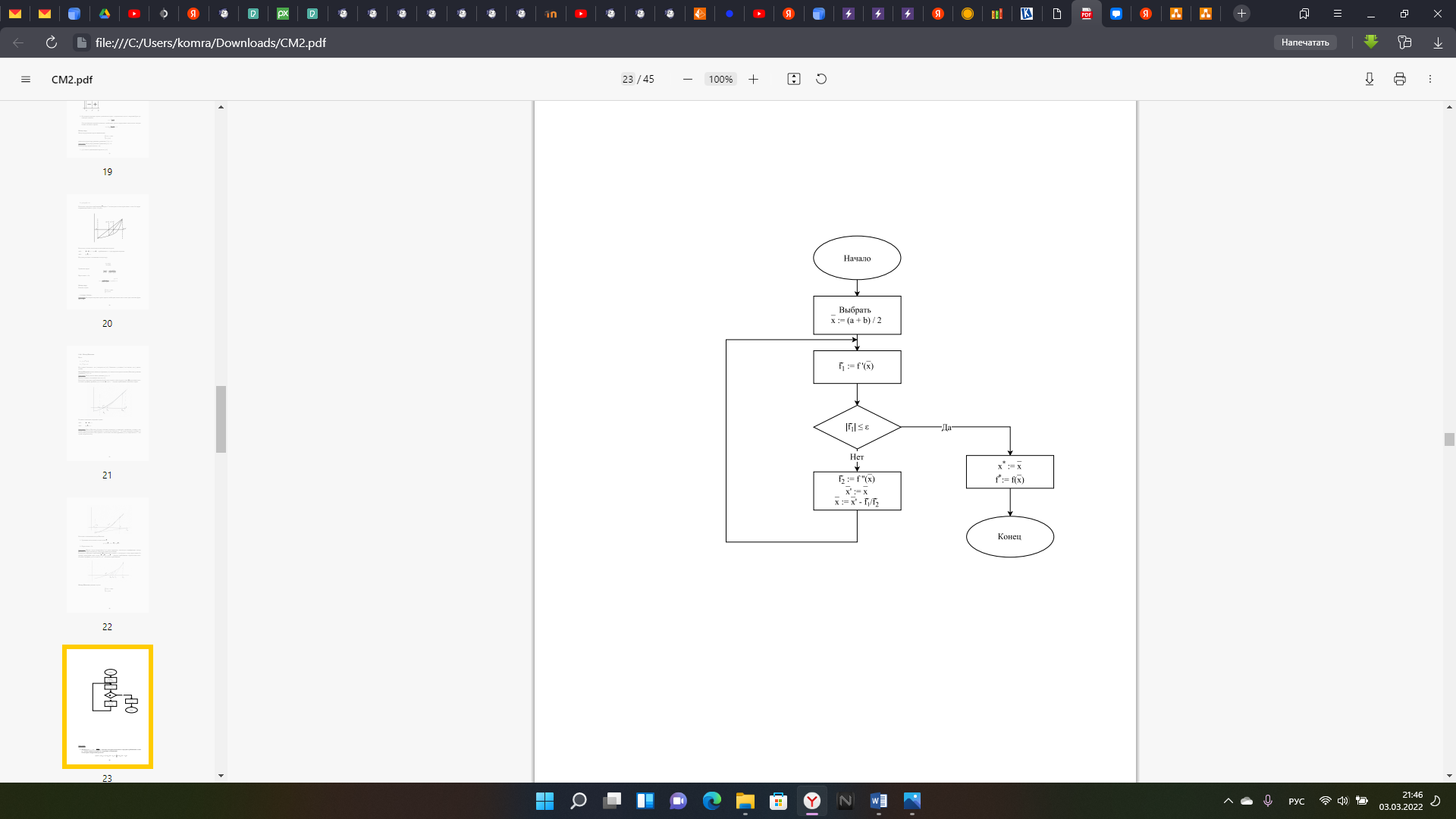

3.4. ФОРМУЛЬНЫЕ РАСЧЁТЫ 2 ИТЕРАЦИИ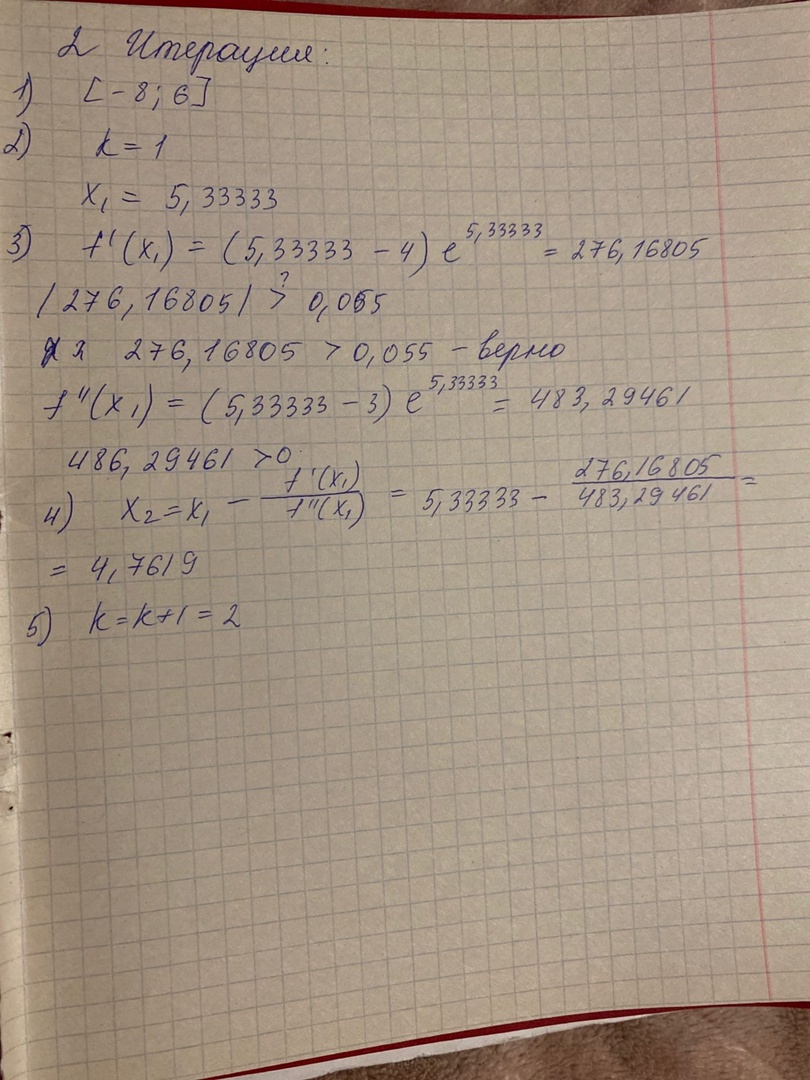

3.5. РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ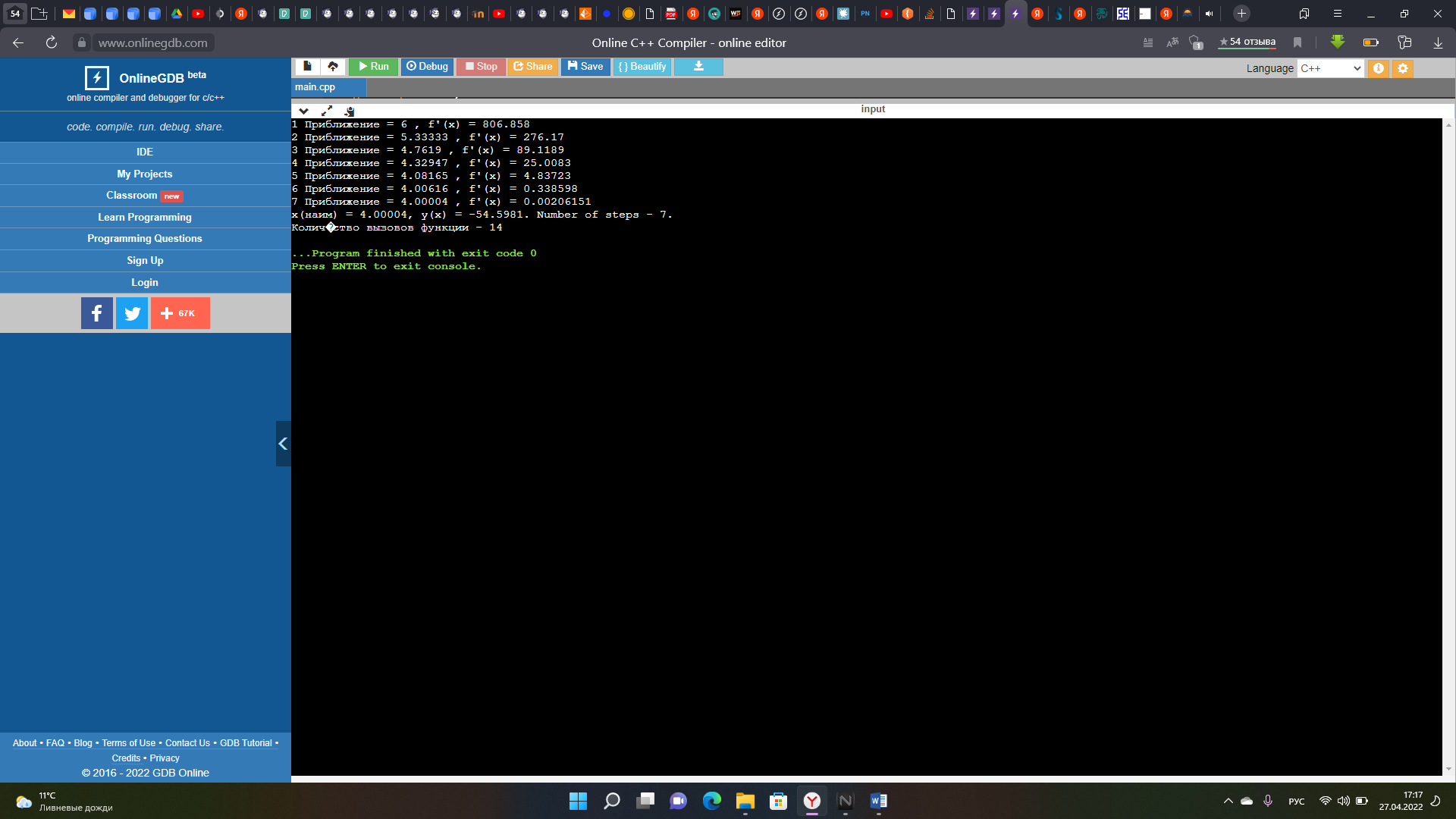

4. СРАВНЕНИЕ АЛГОРИТМОВ

4.1. СРАВНЕНИЕ ПО КОЛИЧЕСТВАМ ОБРАЩЕНИЙ К ФУНКЦИИ

Название метода	Интервал	Обращения к функции	Точность	Значение x
Метод средней точки	[-8; 6]	18	0,001	4,00001
Метод Хорд	[-8; 6]	34853	0,001	3,99998
Метод Ньютона	[-8; 6]	16	0,001	4

4.2. СРАВНЕНИЕ ТОЧНОСТИ ПРИ ЗАДАННОМ КОЛИЧЕСТВЕ ИТЕРАЦИЙ

Название метода	Интервал	Количество итераций	Точность	Значение x
Метод средней точки	[-8; 6]	10	0.000416554	4,00001
Метод Хорд	[-8; 6]	10	0.00402684	-7.99965
Метод Ньютона	[-8; 6]	10	0.0000000778297	4

ЗАКЛЮЧЕНИЕ

Самый быстрый – метод Ньютона. Самый точный – метод Ньютона. Методы средней точки и Ньютона оказались наиболее эффективными, чем метод хорд. Он оказался самым медленным.