Метод наискорейшего спуска. Методы оптимизации. Метод наискорейшего спуска с поиском шага методом средней точки
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
По дисциплине «Методы оптимизации» На тему: «Метод наискорейшего спуска с поиском шага методом средней точки». Оглавление2.Методы первого порядка. 2 2.1.Алгоритм наискорейшего спуска. 2 4.Реализация произвольной функции в MathCad-15. 5 Введение. Методы оптимизации занимаются построением оптимальных решений для математических моделей. В эту дисциплину не входит само построение математических моделей. Но именно вид модели определяет метод или методы, используемые для построения оптимального решения. В большинстве случаев математическую модель объекта можно представить в виде целевой функции  или критерия оптимальности (иногда без ограничений), которую нужно максимизировать или минимизировать. Т.е. необходимо найти максимум или минимум поставленной задачи, причем или критерия оптимальности (иногда без ограничений), которую нужно максимизировать или минимизировать. Т.е. необходимо найти максимум или минимум поставленной задачи, причем  – области возможных значений – области возможных значений 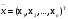 . Как правило, область допустимых значений D задается. Тогда задача формулируется следующим образом: . Как правило, область допустимых значений D задается. Тогда задача формулируется следующим образом:  . .Или по-другому:  , ,при  Область допустимых значений D определяется системой линейных или нелинейных ограничений, накладываемых на 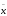  . .В реальных задачах ограничения на область возможных значений переменных модели отсутствуют чрезвычайно редко, потому что, как правило, переменные бывают связаны с некоторым ограниченным ресурсом. Но все-таки с задачами без ограничений сталкиваются. Это бывает в условиях “неограниченных” ресурсов или при наличии условий, не накладывающих ограничений на переменные задачи. В таком случае мы имеем безусловную задачу, задачу без ограничений:  . .Сложность задачи зависит от вида критерия  и функций и функций  ,определяющих допустимую область. Функции могут быть линейными и нелинейными, быть непрерывными или принимать дискретные значения. Область возможных значений может быть выпуклой и невыпуклой, несвязной, представлять собой дискретное множество точек. В зависимости от этого задачи могут быть одноэкстремальными или многоэкстремальными, могут использоваться одни или другие методы поиска решения. ,определяющих допустимую область. Функции могут быть линейными и нелинейными, быть непрерывными или принимать дискретные значения. Область возможных значений может быть выпуклой и невыпуклой, несвязной, представлять собой дискретное множество точек. В зависимости от этого задачи могут быть одноэкстремальными или многоэкстремальными, могут использоваться одни или другие методы поиска решения.Например, если функции  и и  линейны, имеем задачу линейного программирования и можем использовать для поиска решения методы линейного программирования (варианты симплекс-метода). Если функции линейны, имеем задачу линейного программирования и можем использовать для поиска решения методы линейного программирования (варианты симплекс-метода). Если функции  и и  нелинейные, используем методы нелинейного программирования. Если при этом минимизируем выпуклую нелинейные, используем методы нелинейного программирования. Если при этом минимизируем выпуклую  при выпуклых функциях при выпуклых функциях  , то знаем, что задача одноэкстремальна (выпуклое нелинейное программирование). Если , то знаем, что задача одноэкстремальна (выпуклое нелинейное программирование). Если  линейны, а минимизируемая линейны, а минимизируемая  представляет собой квадратичную выпуклую функцию, можем использовать алгоритмы квадратичного программирования. представляет собой квадратичную выпуклую функцию, можем использовать алгоритмы квадратичного программирования. При минимизации вогнутой функции на выпуклой области можем столкнуться с многоэкстремальностью задачи и необходимостью поиска глобального экстремума. Если на переменные, входящие в задачу, наложено требование целочисленности или дискретности, то используются методы дискретного программирования, среди которых наиболее хорошо разработаны методы решения линейных дискретных задач. Если система ограничений отсутствует и  представляет собой нелинейную функцию, то для решения задачи (3), то есть для определения минимума или максимума этой функции используются различные алгоритмы поиска. В зависимости от информации о функции представляет собой нелинейную функцию, то для решения задачи (3), то есть для определения минимума или максимума этой функции используются различные алгоритмы поиска. В зависимости от информации о функции  ) , используемой в алгоритме, могут применяться прямые методы поиска, методы поиска первого или второго порядка. ) , используемой в алгоритме, могут применяться прямые методы поиска, методы поиска первого или второго порядка. Прямые методы поиска или методы нулевого порядка это методы, в которых при поиске экстремума используется информация только о самой функции и не используется информация о ее производных. Плюсом таких методов является возможность оптимизации функций, аналитическое представление которых неизвестно, т.е. эти функции определены только алгоритмически. Методы первого порядка при поиске решения используют не только информацию о самой функции, но и о её производных первого порядка. К таким методам относятся различные градиентные алгоритмы. Методы второго порядка при поиске решения используют информацию о самой функции и о её производных первого и второго порядка. Сюда относятся метод Ньютона и его модификации. Методы первого порядка.К методам первого порядка относятся алгоритмы, в которых в процессе поиска кроме информации о самой функции используется информация о производных первого порядка. К группе таких методов относятся различные градиентные методы. Алгоритм наискорейшего спуска.Градиент функции в любой точке показывает направление наибольшего локального увеличения  . Поэтому при поиске минимума . Поэтому при поиске минимума  , следует двигаться в направлении противоположном направлению градиента , следует двигаться в направлении противоположном направлению градиента  в данной точке, то есть в направлении наискорейшего спуска. Итерационная формула процесса наискорейшего спуска имеет вид: в данной точке, то есть в направлении наискорейшего спуска. Итерационная формула процесса наискорейшего спуска имеет вид: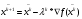 , ,или 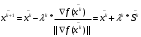 . .Очевидно, что в зависимости от выбора параметра траектории спуска будут существенно различаться (см. рис. 1). 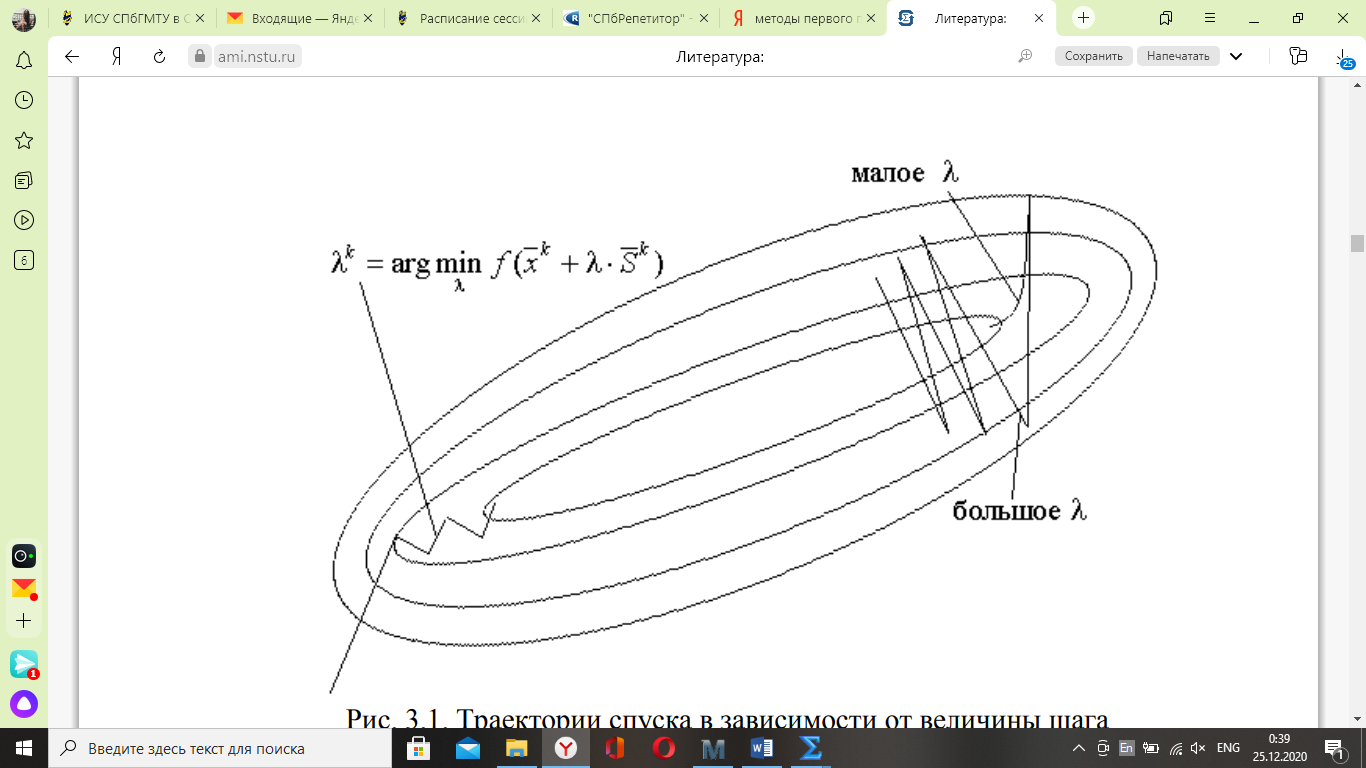 Рис. 1. Рис. 1.Траектории спуска в зависимости от величины шага. При большом значении траектория спуска будет представлять собой колебательный процесс, а при слишком больших процесс может расходиться. При выборе малых траектория спуска будет плавной, но и процесс будет сходиться очень медленно. Обычно выбирают из условия  , ,решая одномерную задачу минимизации с использованием некоторого метода. В этом случае получаем алгоритм наискорейшего спуска. Если определяется в результате одномерной минимизации, то градиент в точке очередного приближения будет ортогонален направлению предыдущего спуска 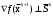 . .Вообще говоря, процедура наискорейшего спуска может закончиться в стационарной точке любого типа, в которой  . Поэтому следует проверять, не завершился ли алгоритм в седловой точке. Эффективность алгоритма зависит от вида минимизируемой функции. Алгоритм наискорейшего спуска сойдется за одну итерацию при любом начальном приближении для функции . Поэтому следует проверять, не завершился ли алгоритм в седловой точке. Эффективность алгоритма зависит от вида минимизируемой функции. Алгоритм наискорейшего спуска сойдется за одну итерацию при любом начальном приближении для функции 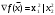 (см. рис. 2). Но сходимость будет очень медленной, например, в случае функции вида (см. рис. 2). Но сходимость будет очень медленной, например, в случае функции вида 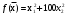 . В тех ситуациях, когда линии уровня минимизируемой функции представляет собой прямолинейный или, хуже того, криволинейный "овраг" эффективность алгоритма оказывается очень низкой. . В тех ситуациях, когда линии уровня минимизируемой функции представляет собой прямолинейный или, хуже того, криволинейный "овраг" эффективность алгоритма оказывается очень низкой. Рис. 2. Рис. 2.Траектории спуска в зависимости от вида функций. Очевидно, что хорошие результаты может давать предварительное масштабирование функций. Процесс наискорейшего спуска обычно быстро сходится вдали от точки экстремума и медленно в районе экстремума. Поэтому метод наискорейшего спуска нередко используют в комбинации с другими алгоритмами. Метод средней точки. Прямые методы используются при минимальных требованиях к целевой функции f(x), которая считается унимодальной, и вычислению подлежат значения только самой функции, но не ее производных. Пусть теперь f(x) является дифференцируемой или дважды дифференцируемой выпуклой функцией и возможно вычисление производных f(x) в произвольно выбранных точках. В этом случае эффективность поиска точки минимума можно существенно повысить. Принимаем во внимание и то, что для выпуклой дифференцируемой функции равенство  является не только необходимым, но и достаточным условием глобального минимума. Поэтому, если известно, что x* является внутренней точкой отрезка [a,b], то приближенное равенство является не только необходимым, но и достаточным условием глобального минимума. Поэтому, если известно, что x* является внутренней точкой отрезка [a,b], то приближенное равенство 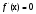 или или  может служить условием остановки вычислений в рассматриваемых трех методах. может служить условием остановки вычислений в рассматриваемых трех методах.Метод средней точки. Если определение производной  не представляет затруднений, то в процедуре исключения отрезков методом дихотомии вычисление двух значений f (x) вблизи середины очередного отрезка можно заменить вычислением одного значения не представляет затруднений, то в процедуре исключения отрезков методом дихотомии вычисление двух значений f (x) вблизи середины очередного отрезка можно заменить вычислением одного значения  в его средней точке в его средней точке  . .Если  , то точка x лежит на участке монотонного возрастания f(x), поэтому , то точка x лежит на участке монотонного возрастания f(x), поэтому 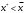 , и точку минимума следует искать на отрезке , и точку минимума следует искать на отрезке . При . При  имеем противоположную ситуацию и переходим к отрезку имеем противоположную ситуацию и переходим к отрезку  . Равенство . Равенство  означает, что точка минимума найдена точно означает, что точка минимума найдена точно  (см. рис. 3). (см. рис. 3). Рис. 3. Рис. 3.Иллюстрация исключения отрезков методом средней точки. Такое исключение отрезков требует на каждой итерации только одного вычисления  и уменьшает отрезок поиска точки x* ровно вдвое. и уменьшает отрезок поиска точки x* ровно вдвое.Алгоритм метода средней точки. Шаг 1. Положить  . Вычислить . Вычислить  . Перейти к шагу 2. . Перейти к шагу 2. Шаг 2. Проверка на окончание поиска: если  , то положить , то положить 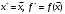 и завершить поиск, иначе перейти к шагу 3. и завершить поиск, иначе перейти к шагу 3.Шаг 3. Сравнить  с нулём: если с нулём: если  , то продолжить поиск на отрезке , то продолжить поиск на отрезке  , положив , положив 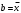 , иначе – на отрезке , иначе – на отрезке  , положив , положив 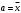 . Перейти к шагу 1. . Перейти к шагу 1. Реализация произвольной функции в MathCad-15.Скриншоты из программы приведены далее, на листах с альбомной ориентацией.  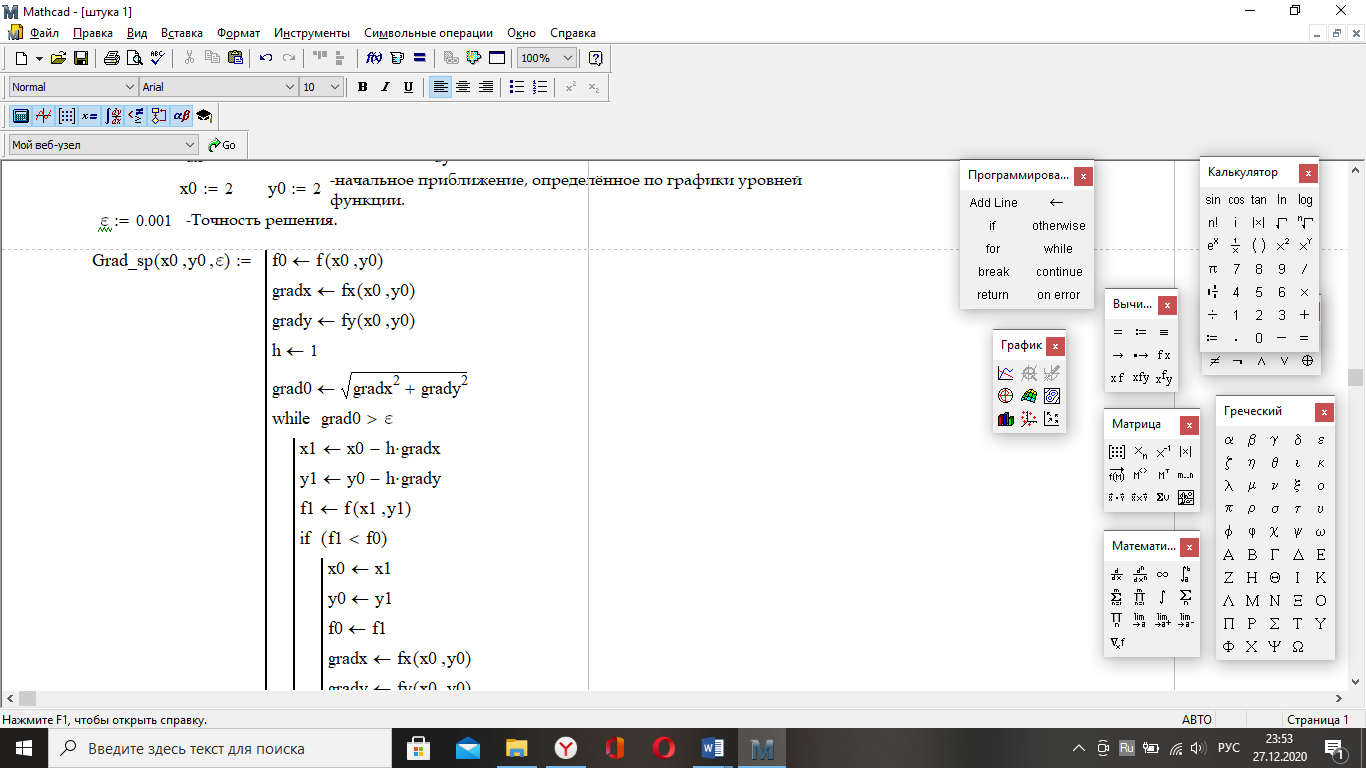  |
