Задача. здача №23 8 вариант. Методическая разработка задачи 23 8 вариант Тип задачи геометрическая. При решении задачи 23 обучающие должны уметь
 Скачать 44.12 Kb.
|
|
Гуляева В.С. 5 курс 3 группа ЗФО Методическая разработка задачи №23 8 вариант Тип задачи: геометрическая. При решении задачи №23 обучающие должны уметь: - применять различные теоретические знания курса геометрии; - выполнять действия с геометрическими фигурами; - математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и объяснения; Трудности и ошибки, которые могут возникнуть при решении задачи: - знание теорем, но неумение применять их на практике; - не правильно построенный чертеж; - не замечание на чертеже уже известных теорем и закономерностей. Способы и методы решения задачи: В ходе решения мы используем геометрический и алгебраический методы решения задачи. Задача. Окружность пересекает стороны АВ и АС треугольника ABC в точках K и P соответственно и проходит через вершины В и С. Найдите длину отрезка KP, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ. Объяснение: 1.Прочитаем задачу. 2. Начертим    B A C 3. Проведем через точки В и С окружность, таким образом, что она пересекает стороны АВ и АС соответственно в точках К и Р. Соединим точки К и Р, получим отрезок КР, длину которого нам и надо найти.     4. По условию нам дано, что АР=34. Кроме этого нам известно, что ВС=  5. Найти нам нужно длину отрезка КР. 6. Рассмотрим четырехугольник PKBC. Заметим, что четырехугольник PKBC вписан в окружность, следовательно, выполняется условие: сумма противоположных углов четырехугольника равна 180° (условие того, что четырехугольник можно вписать в окружность). Т.е. ∠PKB+∠BCP=180° ∠PKB+∠AKP=180° (т.к. это смежные углы). Следовательно, ∠AKP=∠BCP . 7. Рассмотрим треугольники ABC и AKP. ∠AKP=∠BCP (это мы выяснили чуть выше), ∠A - общий, тогда эти треугольники подобны (по признаку подобия). Следовательно 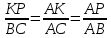 (из определения подобных треугольников). 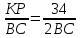Нас интересует равенство    = 17.Ответ: KP=17. |