Методические рекомендации по проведению контрольной работы Составить расчётную схему. Использовать закон Паскаля
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
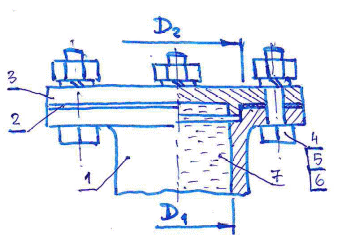
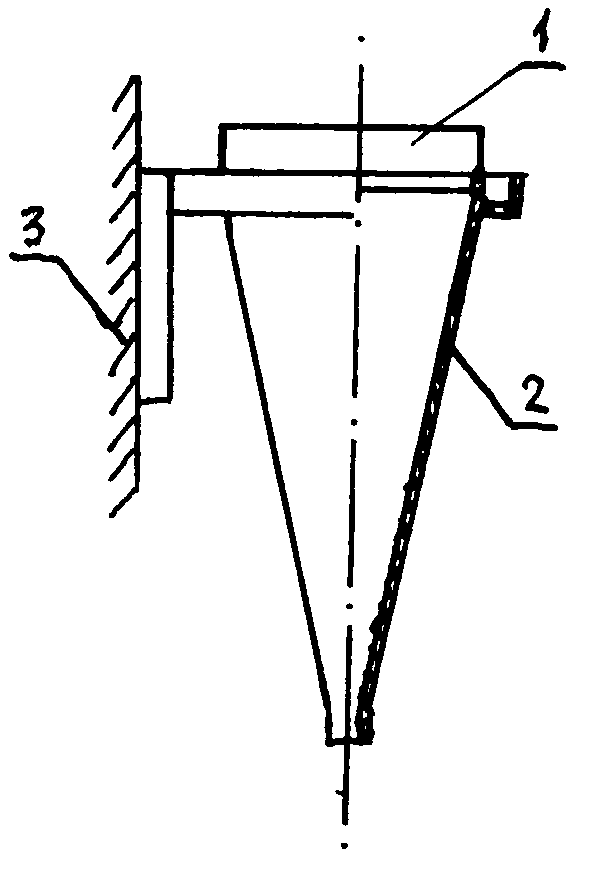
Комплект типовых контрольных заданий Для определения исходных данных используйте номер зачётной книжки (обязательно укажите его на титульном листе). X, Y, Z – три последние цифры номера зачётной книжки, в том случае, когда X·Y·Z=0) подставлять в условие задачи X·Y·Z=1000. Если X·Y=0 подставлять в условия задачи X·Y=100 (аналогично для X·Z, Y·Z, Z·X и других комбинаций. Если Z = 0, подставлять в условие задачи Z=10 (также для X и Y). Тема 1: Физические свойства жидкостей и газов Задача 1.1. Определить силу, действующую на фланец сосуда (рис. 1.1), находящегося под давлением 2,5 МПа. Внутренний диаметр сосуда D1=(100+ X·Y) мм. Внутренний диаметр прокладки D2= D1+20 мм.
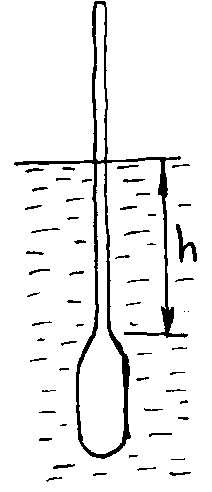
Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать закон Паскаля. Задача 1.2. Определить глубину погружения поплавка цилиндрической формы в воду. Диаметр поплавка d=(10·X+10·Y) мм. Масса поплавка m=(X+10·Y) грамм. Ось поплавка сохраняет вертикальное положение в процессе его погружения. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать закон Архимеда.
Методические рекомендации по проведению контрольной работы: Использовать закон Паскаля. Тема 2: Гидростатика, уравнения Эйлера Задача 2.1. Найти формулу для определения давления на выходе из бака гидравлической системы. Определить величину давления на выходе из бака гидравлической системы, если скорость бульдозера за 20 секунд изменилась с Z км/час до Y км/час. Длина бака 0,6 м, Высота объёма рабочей жидкости в баке относительно оси всасывающего трубопровода 0,5 м. В гидравлической системе бульдозера используется жидкость МГ-15-В(с) плотностью 860 кг/м3.
Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать уравнения Эйлера. Задача 2.2. Найти закон распределения давления в жидкости, находящейся в роторе 1 вертикальной центрифуги. Жидкость 2 вращается вместе с ротором 1 со скоростью ω. 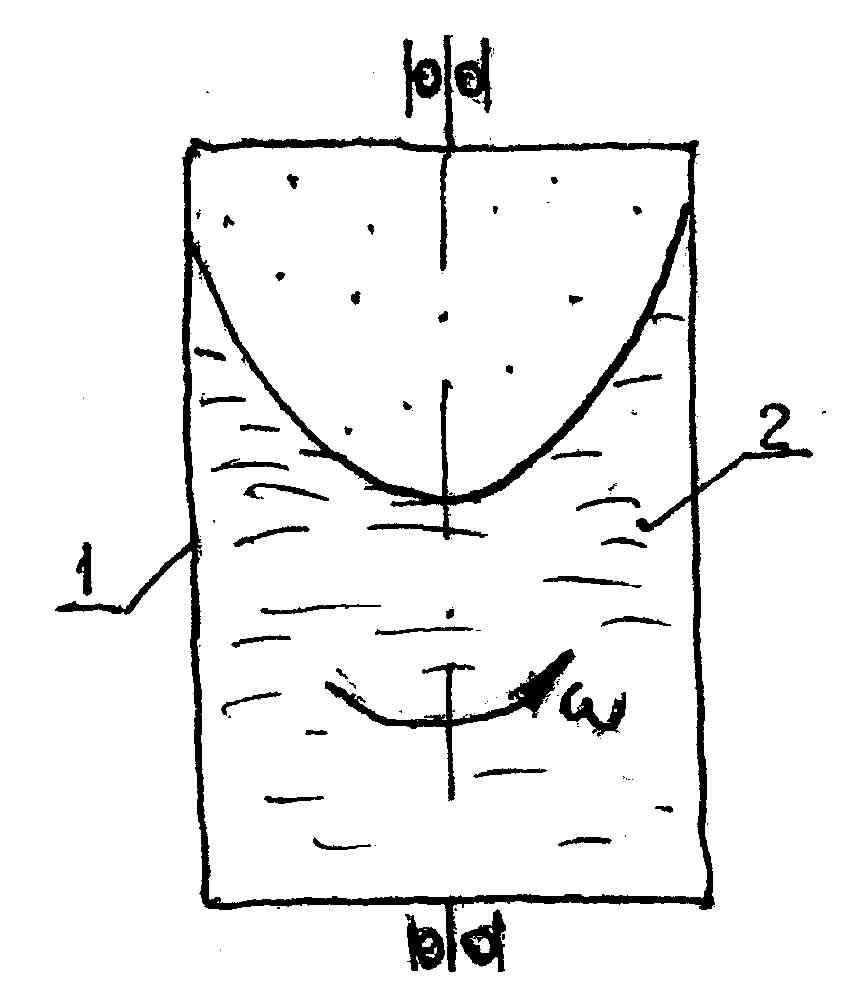 Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать уравнения Эйлера. Тема 3: Течение жидкостей в трубах и щелях Задача 3.1. Ось всасывающего трубопровода насоса длиной (100+X+Y+Z) мм и диаметром (20+X+Y+Z) мм расположена на 0.8 м выше уровня жидкости в ёмкости. Определить давление в конце трубопровода (перед насосом), если расход рабочей жидкости ( 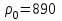 кг/м3, кг/м3, 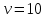 мм2/с), Q=50 л/мин. мм2/с), Q=50 л/мин. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать формулу Хагена-Пуазейля. Задача 3.2. Определить коэффициент потери температуры трубопровода длиной (100+3·(X+Y+Z)) км. Температура жидкости в начале трубопровода Т1=39 °С, в конце Т=20 °С, температура окружающей среды – 40 °С, Методические рекомендации по проведению контрольной работы: Использовать формулу В. Г. Шухова. Тема 4: Уравнение Я. Бернулли Задача 4.1. По горизонтальной трубе диаметром 100 мм, имеющей сужение d=40 мм, движется вода в количестве 6 л/с. Определить давление в узком сечении, если напор воды перед сужением равен (Z+1) м. Потерями напора пренебречь. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать уравнение Бернулли. Задача 4.2. Определить потери давления внутри полого поршня циркуляционного клапана винтового забойного двигателя. Скорость жидкости внутри поршня U=Z м/с; вязкость 0,1·Y Па·с; плотность (1000+100·X) кг/м3. Принять L = 130 мм.
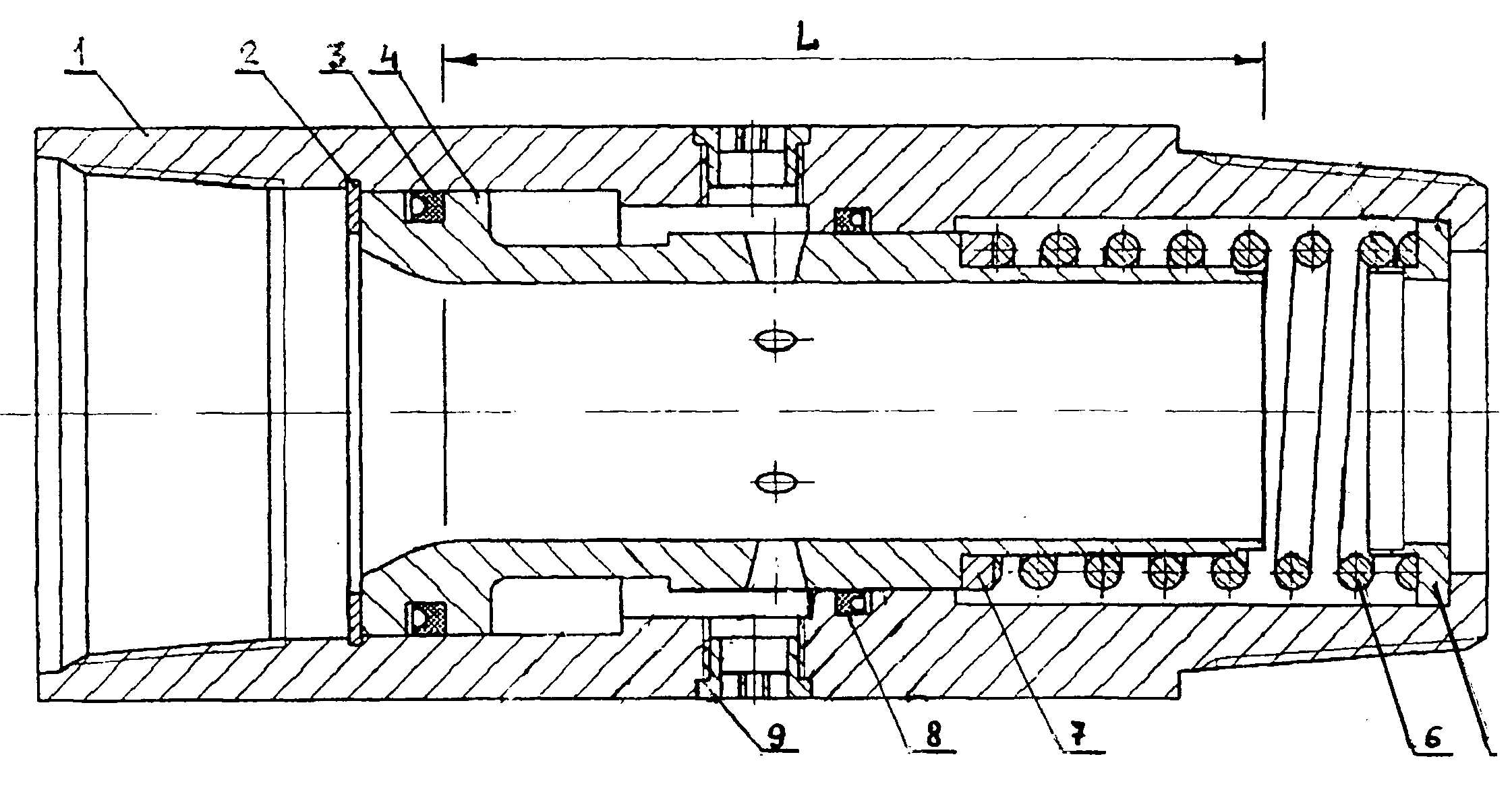 Рис. 4.2. Основные элементы циркуляционного клапана: 1 - корпус; 2 – кольцо стопорное; 3 и 8 – уплотнители; 4 – поршень с отверстием; 5 и 7 – шайбы упорные; 6 – пружина; 9 - фильтр. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать уравнение Бернулли. Тема 5: Истечение жидкости из сосудов. Элементы теории струй Задача 5.1. Записать процесс вывода формулы, описывающей истечение жидкости при переменном напоре, из сосуда конической формы (из воронки Марша).
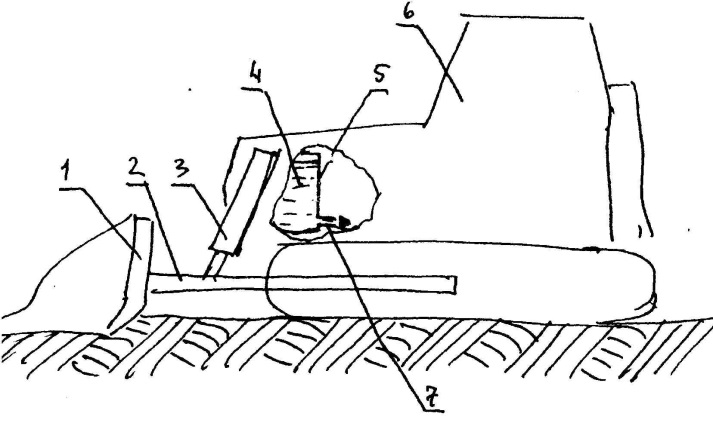
Методические рекомендации по проведению контрольной работы: Объём dV, вытекающий из воронки за время dt, принять равным 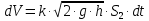 , где К - коэффициент; g – ускорение свободного падения; h - высота поверхности жидкости в воронке Марша относительно вершины конуса; S2 – площадь отверстия. , где К - коэффициент; g – ускорение свободного падения; h - высота поверхности жидкости в воронке Марша относительно вершины конуса; S2 – площадь отверстия.Задача 5.2. Определить силу, действующую на забой. Средняя скорость гидромониторной струи (10+X+Y) м/с, производительность 50 л/с. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать закон сохранения энергии. Тема 6: Гидравлический удар Задача 6.1. Найти величину давления, возникающего в стальном трубопроводе (рис. 6.1), при гидравлическом ударе. Внутренний диаметр трубы dу = 200 мм; толщина стенки трубы δ = 4 мм, скорость движения жидкости U = 0,5·Z м/с, плотность жидкости ρ = 860 кг/м3, номинальное давление pн =0,5·Y кГ/см2, модуль упругости жидкости Еж = X·109 Па, модуль упругости материала трубы Ет = 2·1011 Па.  Рис. 6.1. Фрагмент трубопровода на ММП: 1 – труба; 2 – опора с термостабилизаторами; 3 – насосная станция. Методические рекомендации по проведению контрольной работы: Использовать формулы Н. Е. Жуковского. Задача 6.2. Определить собственную частоту колебаний жидкости между стенками тройника и дросселя. Стволовые задвижки считать открытыми. Принять среднюю толщину стенки равной 10 мм.
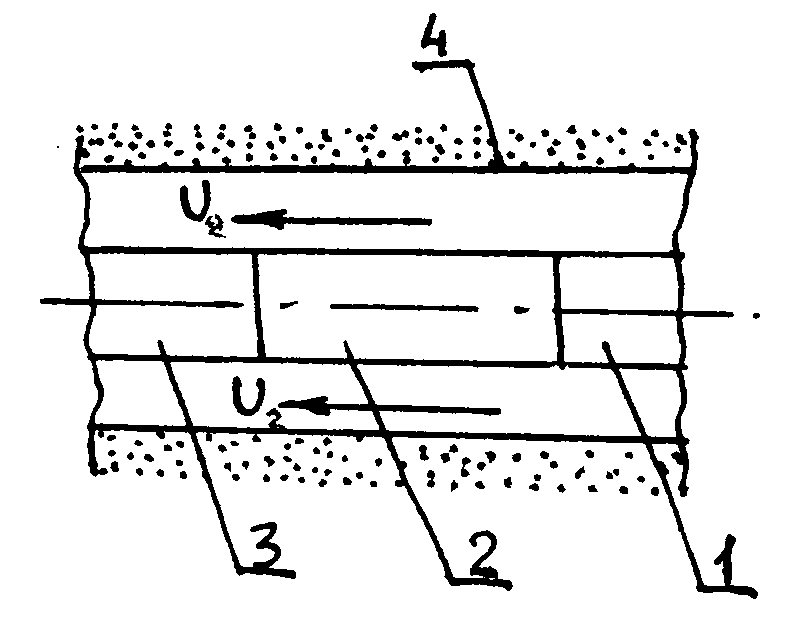
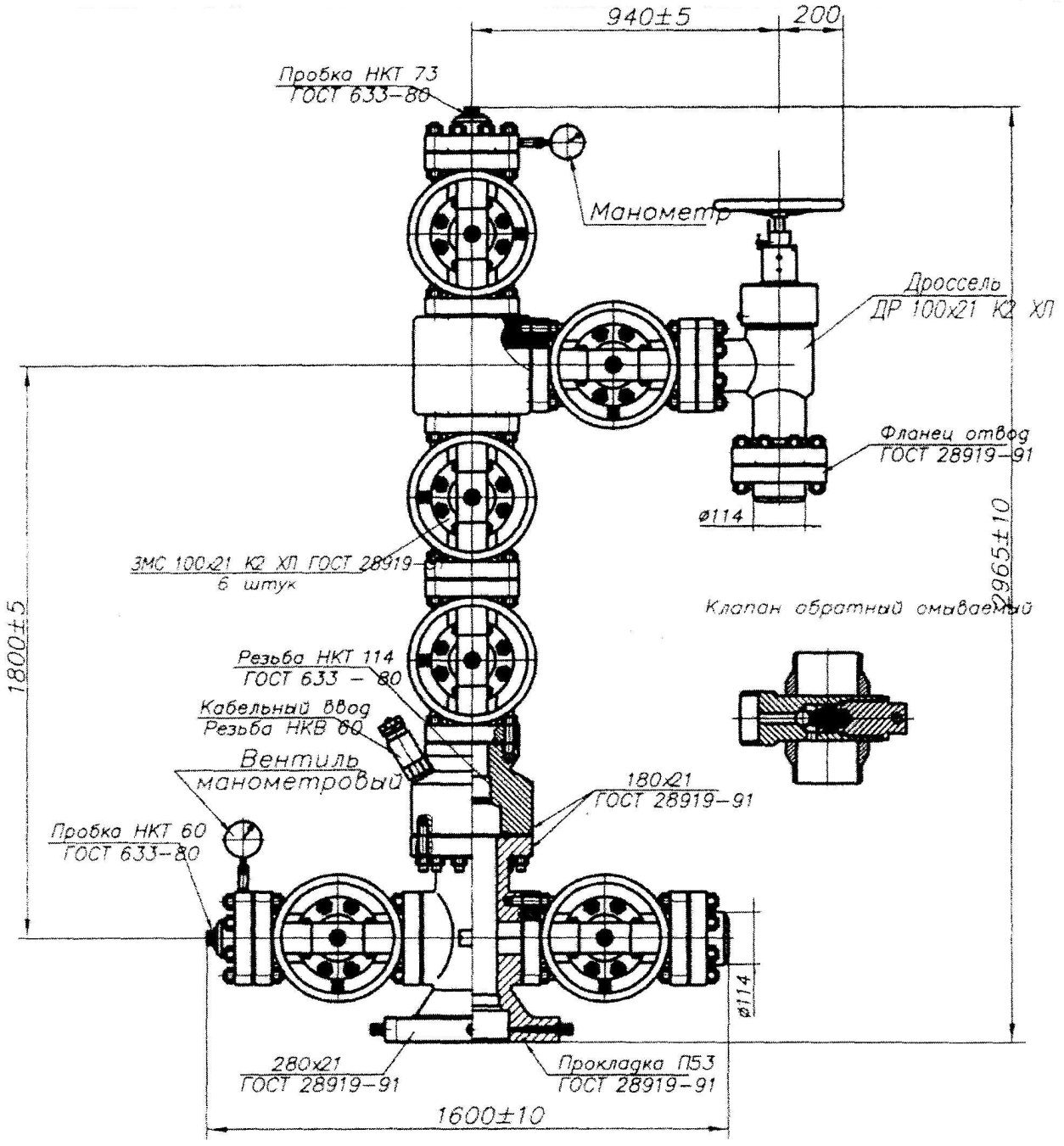 Рис. 6.2. Пример схемы фонтанной арматуры к расчёту собственной частоты колебаний жидкости между элементами. Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать формулы Н. Е. Жуковского. Тема 7: Элементы теории размерностей Задача 7.1. Для использования π-теоремы сформировать безразмерные комплексы: 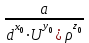 , , 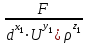 , , 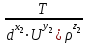 , где a - ускорение; F – сила; Т – крутящий момент. , где a - ускорение; F – сила; Т – крутящий момент. Методические рекомендации по проведению контрольной работы: Использовать алгоритм определения коэффициентов безразмерных комплексов. Задача 7.2. Для использования π-теоремы сформировать безразмерные комплексы: 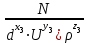 , , 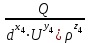 , , 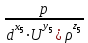 , где N – мощность; Q - расход; p - давление. , где N – мощность; Q - расход; p - давление.Методические рекомендации по проведению контрольной работы: Использовать алгоритм определения коэффициентов безразмерных комплексов. Тема 8: Элементы теории подобия Задача 8.1. Определить расход воды в трубе диаметром 250 мм, имеющей плавное сужение до диаметра 125 мм, если показания пьезометров расходомера Вентури: до сужения 50 см; после сужения 30 см. Потерями напора пренебречь. Как нужно изменить расход жидкости в трубе, если диаметр трубы уменьшили в десять раз, чтобы критерий Рейнольдса остался неизменным? Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать уравнение Даниила Бернулли, критерий Рейнольдса и основные правила теории подобия. Задача 8.2. По трубе диаметром 40 мм движется жидкость в количестве (25,9-Z) л/с. Вязкость жидкости Y мм2/с. Найти внутренний диаметр гидродинамической модели трубы, по которой проходит 2 л/с жидкости с вязкостью 1 мм2/с. Методические рекомендации по проведению контрольной работы: Использовать критерий Рейнольдса. Тема 9: Элементы теории плавания тел
Методические рекомендации по проведению контрольной работы: Составить расчётную схему. Использовать закон Архимеда. Критерии оценивания: - оценка «отлично» выставляется, если расчётная схема составлена с правильно нанесёнными размерами, скоростями, силами и другими элементами; формулы, необходимые для решения задачи, правильно выведены или подобраны из лекционного материала или литературных источников; исходные данные, взятые из условия задачи или из литературных источников, правильно и в системе СИ подставлены в формулы; результат расчёта правильно вычислен и проанализирован; студент исчерпывающе, точно, логически стройно излагает процесс решения задачи, демонстрируя наличие компетенций, сформированных не менее, чем на 90 процентов. - оценка «хорошо» - если расчётная схема составлена с правильно нанесёнными размерами, скоростями, силами и другими элементами; формулы, необходимые для решения задачи, правильно выведены или подобраны из лекционного материала или литературных источников; исходные данные, взятые из условия задачи или из литературных источников, правильно и в системе СИ подставлены в формулы; результат расчёта правильно вычислен и проанализирован; студент излагает процесс решения задачи, демонстрируя наличие компетенций, сформированных не менее, чем на 75 процентов. - оценка «удовлетворительно» - если расчётная схема составлена с правильно нанесёнными размерами, скоростями, силами и другими элементами; формулы, необходимые для решения задачи, правильно выведены или подобраны из лекционного материала или литературных источников; исходные данные, взятые из условия задачи или из литературных источников, в целом правильно и в системе СИ подставлены в формулы; студент излагает процесс решения задачи, демонстрируя наличие компетенций, сформированных не менее, чем на 60 процентов. - оценка «неудовлетворительно» - если расчётная схема составлена с правильно нанесёнными размерами, скоростями, силами и другими элементами; формулы, необходимые для решения задачи, выведены с ошибками или неверно подобраны из лекционного материала или литературных источников; исходные данные, взятые из условия задачи или из литературных источников, подставлены в формулы не в системе СИ, результат расчётов неверен. Разработчик _________________ П. М. Кондрашов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||