контрльая. Методические указания для выполнения контрольной работы по дисциплине цифровая обработка сигналов

• Название: Методические указания для выполнения контрольной работы по дисциплине цифровая обработка сигналов
• Анкор: контрльая
• Дата: 31.05.2022
• Размер: 270 Kb.
• Имя файла: Kontrolnaya_rabota_TsOS (4).doc
• Тип: Методические указания; #559514

Министерство науки и высшего образования РФ

Пермский национальный исследовательский политехнический университет

Электротехнический факультет

Кафедра «Автоматика и телемеханика»

ФРЕЙМАН Владимир Исаакович

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для выполнения контрольной работы
по дисциплине
«ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»
Предназначено для студентов

заочной и заочной ускоренной форм обучения

по направлению подготовки

11.03.02 «Инфокоммуникационные технологии и системы связи»,

профиль «Сети связи и системы коммутации»

Пермь, 2019

Задание № 1. Дискретные сигналы и системы

Дано: сигнал x(t) = x₁(t) + x₂(t) = A₁∙sin (2∙∙f₁∙t) + A₂∙sin (2∙∙f₂∙t),

где A₁ = № /10; A₁ = № /5; f₁ = № (Гц); f₂ = 3∙№ (Гц); № – номер в списке студенческой группы.

Задание:

1. Рассчитать минимальную частоту дискретизации f_{s min} = 2∙(f₂ – f₁).

2. Рассчитать реальную частоту дискретизации f_s = [2∙f_{s min}], где [ ] – операция округления ближайшего большего целого числа (в большую сторону).

3. Рассчитать шаг дискретизации t_s = 1/f_s.

4. Определить количество отсчетов N = [T₁/t_s], где Т₁ = 1/f₁ – период сигнала x₁(t).

5. Выполнить дискретизацию (рассчитать значения функции x(n∙t_s), где n  [0; N–1], и занести результаты расчетов в таблицу).

6. Построить графики:

– функции x₁(t);

– функции x₂(t);

– функции x(t);

– функции x(n∙t_s).

7. Построить спектры:

– функции x₁(t);

– функции x₂(t);

– функции x(t);

– функции x(n∙t_s).

Для расчетов можно воспользоваться любой программой для построения графиков онлайн или приложенным файлом «ЦОС.xls», вкладка «Задание № 1»), внеся в него свои данные (№). График функции x(n∙t_s), который представляет собой точки (отсчеты) совместить с графиком функции x(t).

Задание № 2. Цифровые фильтры с конечной импульсной характеристикой

Дано:

– тип цифрового фильтра: КИХ (фильтр с конечной импульсной характеристикой);

– количество ветвлений фильтра M = (№ mod 4) + 3, где № – номер в списке студенческой группы; mod – операция вычисления остатка от деления;

– значения коэффициентов h(k) = const = 1/M (фильтр среднего значения), k  [0; M–1].

Задание.

1. Построить разностное уравнение (см. п. 4.1, стр. 37).

2. Построить структурную схему (рис. 4.2, стр. 39).

3. Рассчитать импульсную характеристику – значение выхода y(n) для входной последовательность x(n): 1 0 0 ... 0, где количество нулей после единицы равно М. Данные занести в таблицу (см. файл «ЦОС.xls», вкладка «Задание № 2»).
Пример 1.

№ = 14: M = ((14 + 4) mod 5) + 2 =(18 mod 5) + 2 = 3 + 2 = 5.

h(k) = const = 1/5 = 0,2; k  [0; 4].

1. М = 5:



2. Структурная схема фильтра для М = 5 (задержка – элемент памяти, запоминающее устройство на одно значение x(n–k)).


3. Построение импульсной характеристики.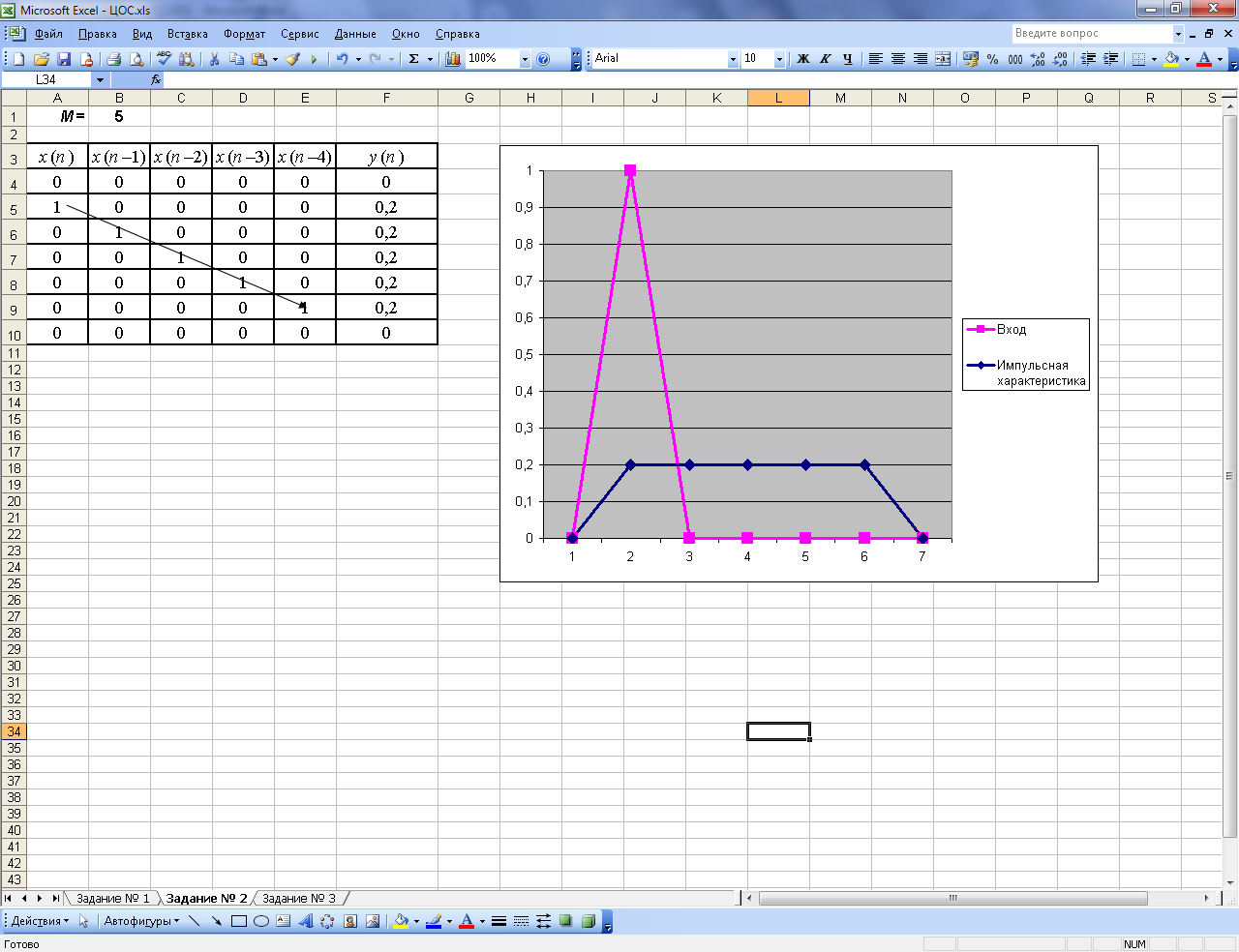

Задание № 3. Цифровые фильтры с бесконечной импульсной характеристикой

Дано:

– тип цифрового фильтра: БИХ (фильтр с бесконечной импульсной характеристикой);

– количество ветвлений фильтра по входу M = (№ mod 4) + 2, где № – номер в списке студенческой группы; mod – операция вычисления остатка от деления;

– количество ветвлений фильтра по выходу N = (№ mod 2) + 1, где № – номер в списке студенческой группы; mod – операция вычисления остатка от деления;

– значения коэффициентов (см. п. 4.2, стр. 43): b(i) = const = 1/M, i  [0; M–1]; a(j) = const = 1/N, j  [1; N].

Задание.

1. Построить разностное уравнение (см. п. 4.2, стр. 43).

2. Построить структурную схему.

3. Рассчитать импульсную характеристику – значение выхода y(n) для входной последовательность x(n): 1 0 0 ... 0, где количество нулей после единицы равно (2·М). Данные занести в таблицу (см. файл «ЦОС.xls», вкладка «Задание № 3»).
Пример 2.

№ = 11: M = (11 mod 5) + 2 =1 + 2 = 3; N = (11 mod 2) + 1 =1 + 1 = 2.

b(i) = const = 1/3 = 0,33, i  [0; 2]; a(j) = const = 1/2 = 0,5, j  [1; 2].

1. М = 3; N = 2: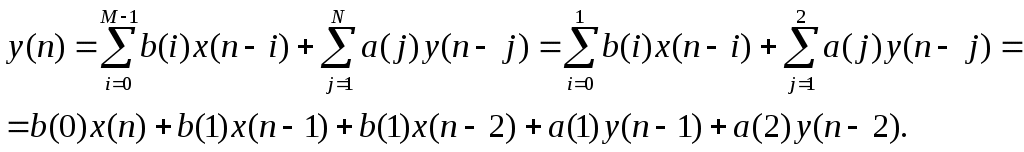



2. Структурная схема фильтра для М = 3, N = 2 .



3. Построение импульсной характеристики.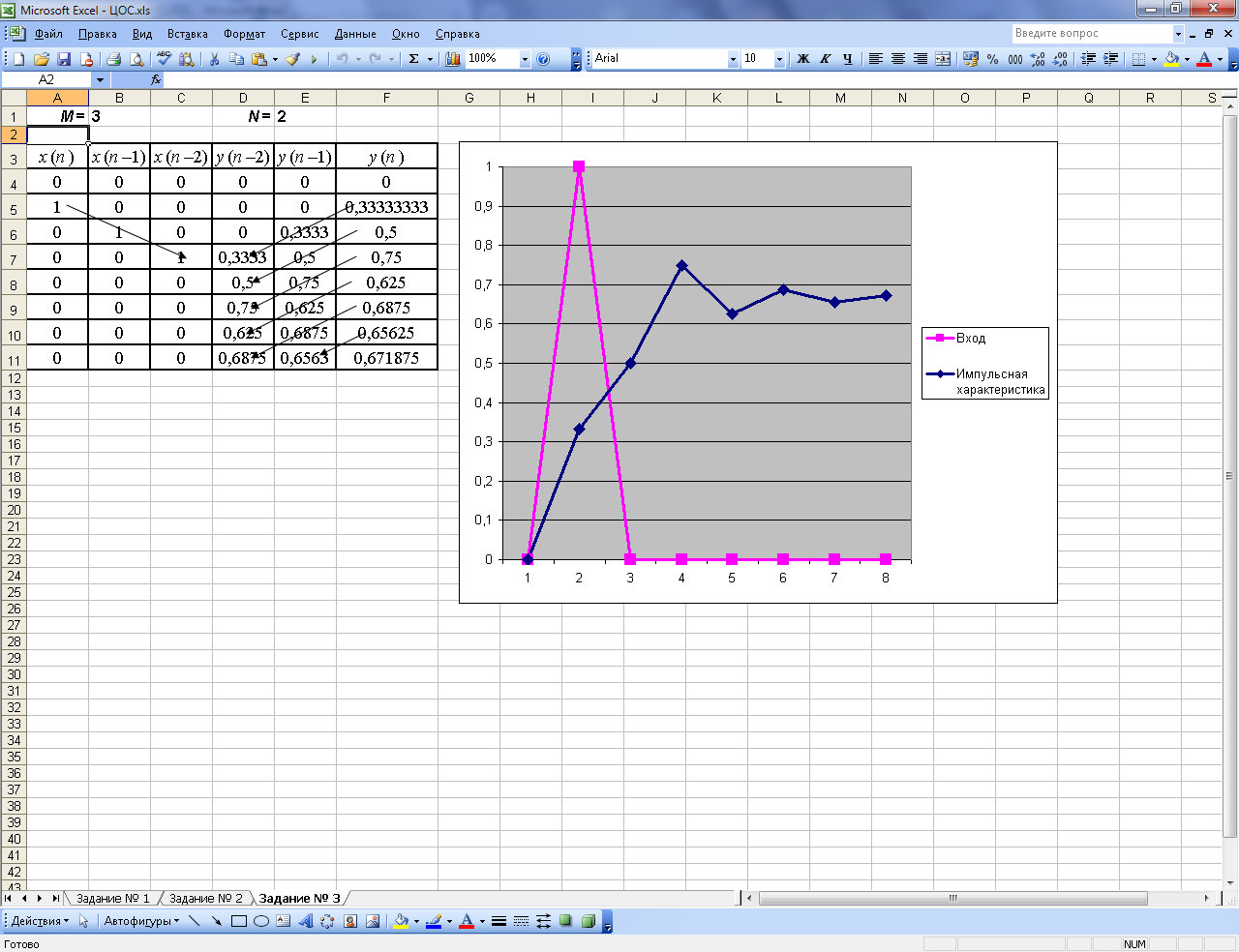